解读《视觉SLAM十四讲》,带你一步一步入门视觉SLAM—— 第 3 讲 三维刚体运动 (上)
上一讲是初识SLAM,如果你还觉得SLAM很简单,那么从这一讲开始,可能问题就要变得棘手了。不过万事开头难,坚持下去终究会守得云开见月明!
第3讲 三维刚体的运动
原书主要内容
在这一讲中,作者原书主要介绍了:
- 三维刚体运动的数学描述方法,包括旋转矩阵、变换矩阵、四元数、欧拉角;
- 以及一种C++常用的数学矩阵运算库Eigen。
解读
点和向量
原书中作者首先介绍了旋转矩阵,在介绍旋转矩阵之前,做了一些铺垫工作,其中介绍了点和向量,这两个东西的概念,我们在高中时候就已经学过了,但是你可能对它们有误解。
点就很简单了,以至于我都不知道怎么解释。向量就是空间中一个有方向有长度的有向线段。这俩就这么简单,它们本身和坐标没有任何关系,当我们想要通过数学的方法去表示或者量化它们的时候,它们才和坐标产生关系。所以坐标并不是向量,也不是点,坐标只是一种表示它们的方法。
坐标系的欧式变换
个人感觉作者对于坐标系的变换讲的并不是很容易懂,比方说作者书中提到,视野中的某个向量 p p p,但是他在图中画的却是一个点,感觉有些这样的地方还是会对理解产生一些障碍。
首先先说一下,刚体运动在SLAM中的应用。比方说你是一个小机器人,你从零时刻开始运动,那么下一时刻,你的位置发生了变化,并且你的姿态也发生了变化。位置的变化很容易刻画,就是平移向量,但是你的姿态就不太容易描述了,你是歪着的,侧着的,横着的,而这一讲就是在解决这个问题。
如下图,首先有一个固定的坐标系 O − x y z O-xyz O−xyz,它和坐标系 O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′之间存在转换关系,也就是说这种转换关系可以把 O − x y z O-xyz O−xyz变到 O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′的位置和姿态。
为了表述的方便,后面我就直接用三维坐标的位姿(位置+姿态)来表示机器人的位姿。其中我们把 O − x y z O-xyz O−xyz看作是世界坐标系,也就是固定坐标系。

平移向量
对于两个坐标系之间的位置变化,直接用平移向量就可以表示,例如下图:
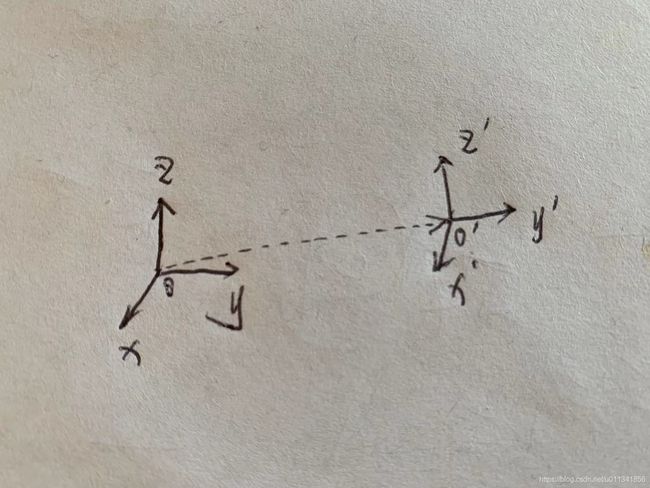
两个坐标系之间位置的变化就对应的是向量 O O ′ OO' OO′, O O ′ OO' OO′也就是平移向量。
旋转矩阵
坐标系 O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′坐标系相对于 O − x y z O-xyz O−xyz坐标系不但有位置变化,还发生了一些转动,这个转动可以使用旋转矩阵来表示。
在这里我借用《十四讲》的方法介绍,但是为了方便理解,我加入一些中间过程:

如上图所示,两个坐标系和一个向量,向量 p ⃗ \vec p p分别可以在两个坐标系中表示,当我们在其中任一个坐标系中表示它时,都需要将 p ⃗ \vec p p的起点移到坐标系的原点处.
对于在 O − x y z O-xyz O−xyz坐标系下,我们可以把向量 p ⃗ \vec p p用如下坐标表示:
[ a 1 a 2 a 3 ] (1) \left[\begin{matrix}a_1\\a_2\\a_3\end{matrix}\right] \tag1 ⎣⎡a1a2a3⎦⎤(1)
对于在 O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′坐标系下,我们可以把向量 p ⃗ \vec p p用如下坐标表示:
[ a 1 ′ a 2 ′ a 3 ′ ] (2) \left[\begin{matrix}a_1'\\a_2'\\a_3'\end{matrix}\right]\tag2 ⎣⎡a1′a2′a3′⎦⎤(2)
O − x y z O-xyz O−xyz坐标系的单位正交基为: [ e ⃗ 1 , e ⃗ 2 , e ⃗ 3 ] [\vec e_1,\vec e_2,\vec e_3] [e1,e2,e3];
O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′坐标系的单位正交基为: [ e ⃗ 1 ′ , e ⃗ 2 ′ , e ⃗ 3 ′ ] [\vec e_1',\vec e_2',\vec e_3'] [e1′,e2′,e3′]。
由于向量不管在什么坐标系下表示,都不会改变向量本身的性质。所以在这两个坐标系下表示的向量 p ⃗ \vec p p是完全相等的,于是就可以得到如下的等式:
[ e ⃗ 1 , e ⃗ 2 , e ⃗ 3 ] ∗ [ a 1 a 2 a 3 ] = [ e ⃗ 1 ′ , e ⃗ 2 ′ , e ⃗ 3 ′ ] ∗ [ a 1 ′ a 2 ′ a 3 ′ ] (3) \left[\begin{matrix}\vec e_1,\vec e_2,\vec e_3 \end{matrix}\right] *\left[\begin{matrix}a_1\\a_2\\a_3\end{matrix}\right] = \left[\begin{matrix}\vec e_1',\vec e_2',\vec e_3' \end{matrix}\right] *\left[\begin{matrix}a_1'\\a_2'\\a_3'\end{matrix}\right]\tag3 [e1,e2,e3]∗⎣⎡a1a2a3⎦⎤=[e1′,e2′,e3′]∗⎣⎡a1′a2′a3′⎦⎤(3)
等式的左边,乘在一起 [ a 1 e ⃗ 1 , a 2 e ⃗ 2 , a 3 e ⃗ 3 ] [a_1\vec e_1, a_2\vec e_2,a_3\vec e_3] [a1e1,a2e2,a3e3],这就是向量 p ⃗ \vec p p采用 O − x y z O-xyz O−xyz坐标系下的采用单位正交基的表示方法。(3)式的右边也是一样的道理。
将(3)式同时左乘 [ e ⃗ 1 ′ T e ⃗ 2 ′ T e ⃗ 3 ′ T ] \left[\begin{matrix}\vec e_1'^T\\\vec e_2'^T\\\vec e_3'^T\end{matrix}\right] ⎣⎡e1′Te2′Te3′T⎦⎤,那么就可以得到下式:
[ e ⃗ 1 ′ T e ⃗ 1 e ⃗ 1 ′ T e ⃗ 2 e ⃗ 1 ′ T e ⃗ 3 e ⃗ 2 ′ T e ⃗ 1 e ⃗ 2 ′ T e ⃗ 2 e ⃗ 2 ′ T e ⃗ 3 e ⃗ 3 ′ T e ⃗ 1 e ⃗ 3 ′ T e ⃗ 2 e ⃗ 3 ′ T e ⃗ 3 ] [ a 1 a 2 a 3 ] = [ a 1 ′ a 2 ′ a 3 ′ ] (4) \left[\begin{matrix} \vec e_1'^T\vec e_1 & \vec e_1'^T\vec e_2 &\vec e_1'^T\vec e_3\\ \vec e_2'^T\vec e_1 & \vec e_2'^T\vec e_2 &\vec e_2'^T\vec e_3\\ \vec e_3'^T\vec e_1 & \vec e_3'^T\vec e_2 &\vec e_3'^T\vec e_3 \end{matrix} \right] \left[\begin{matrix}a_1\\a_2\\a_3\end{matrix}\right]= \left[\begin{matrix}a_1'\\a_2'\\a_3'\end{matrix}\right] \tag4 ⎣⎡e1′Te1e2′Te1e3′Te1e1′Te2e2′Te2e3′Te2e1′Te3e2′Te3e3′Te3⎦⎤⎣⎡a1a2a3⎦⎤=⎣⎡a1′a2′a3′⎦⎤(4)
(4)式的3x3矩阵就是表示两个坐标系之间的姿态变化,进一步简写为:
R [ a 1 a 2 a 3 ] = [ a 1 ′ a 2 ′ a 3 ′ ] (5) R \left[\begin{matrix}a_1\\a_2\\a_3\end{matrix}\right]= \left[\begin{matrix}a_1'\\a_2'\\a_3'\end{matrix}\right] \tag5 R⎣⎡a1a2a3⎦⎤=⎣⎡a1′a2′a3′⎦⎤(5)
R R R就表示了,由于坐标系的姿态变化,给向量 p ⃗ \vec p p在两个坐标系下的坐标带来了怎样的变化, R R R也就代表了两个坐标系之间姿态的变化,请注意并没有代表平移变化。
齐次坐标
齐次坐标主要是透视空间中的概念。实际上我们一直在学习的欧式几何空间只是透视空间的子集合。我们知道,在欧式空间中两条平行线在无穷远处是不会相交的,但是实际生活中,两条平行的铁轨在无穷远处是相交在一起的。像这种现象在欧式空间中是不能描述的,只能在透视空间中描述。如果想进一步了解齐次坐标,可以学习这篇内容《什么是齐次坐标系?为什么要用齐次坐标系?》
而齐次坐标的引入,可以将我们从欧式空间中的一个问题,提升到更大维度的空间中去,也就是透视空间。对于《十四讲》中的其次坐标的引入,可以解决在三维欧式空间中不能线性运算的问题。
变换矩阵
在透视空间中,可以把旋转和平移放在一个矩阵中,然后进行一些线性的运算,可以非常方便的解决欧式空间下的一些计算不方便的问题。
变换矩阵的形式:
T = [ R 3 ∗ 3 t 3 ∗ 1 0 T 1 ] T = \left[\begin{matrix}R_{3*3} & t_{3*1}\\ 0^T & 1 \end{matrix} \right] T=[R3∗30Tt3∗11]
变换矩阵是一个4x4的矩阵,它包含了旋转矩阵 R R R和平移矩阵 t t t,对于一个齐次坐标的向量 [ a ⃗ 1 ] \left[\begin{matrix}\vec a\\1 \end{matrix}\right] [a1],可以直接通过变换矩阵来改变它到另外一个坐标系下:
[ a ⃗ ′ 1 ] = [ R t 0 T 1 ] [ a ⃗ 1 ] \left[\begin{matrix}\vec a'\\1 \end{matrix}\right] = \left[\begin{matrix}R & t\\ 0^T & 1 \end{matrix} \right] \left[\begin{matrix}\vec a\\1 \end{matrix}\right] [a′1]=[R0Tt1][a1]
实践
关于Eigen的使用,如果你对C++模板类编程熟悉的话,应该不会产生什么障碍。如果你真的对它不熟悉的话,也别着急,你先学会书中的用法,暂且别管原因。
在使用Eigen进行矩阵运算时,一定要注意维度的问题,大多数的错误都是因为不满足矩阵运算维度的要求。
你可以在《十四讲》的GitHub仓库中(地址)把代码下载下来,找到本讲对应的代码,然后将它编译运行。编译运行之前,请先按照书本要求安装Eigen库。编译过程(以后所有的CMake工程都是按照这样方法编译):
- 第一步在对应代码的目录下新建一个名为
build的目录; - 然后进入
build目录,打开终端将工作目录变换到当前目录下; - 在终端中使用命令
cmake ..进行预编译 - 然后继续使用命令
make进行编译 - 然后运行编译之后产生的可执行文件,就可以看到效果了,运行代码为
./xxxx,其中xxxx为可执行文件的名称。
关于Eigen的使用,我有一点需要补充,当你学习到深处的时候,可能会用Eigen去做大型矩阵的运算,这个时候可能会出一些问题,比方说你定义了一个大型矩阵Eigen::Matrix,而你用它做一些运算的时候,会报错,这就是因为栈溢出的原因,解决方法,可以参考我的另外一篇博客《Eigen在使用高维矩阵时栈溢出,报错OBJECT_ALLOCATED_ON_STACK_IS_TOO_BIG,解决方法及高维矩阵运算》,当前当前阶段你可能不会碰到这个问题,但是当你碰到的时候,你不妨参考一下我的解决方法!
一个人只要强烈地坚持不懈地追求,他就能达到目的。——司汤达
参考资料
1.Eigen在使用高维矩阵时栈溢出,报错OBJECT_ALLOCATED_ON_STACK_IS_TOO_BIG,解决方法及高维矩阵运算
2.什么是齐次坐标系?为什么要用齐次坐标系?
3.《视觉SLAM十四讲 从理论到实践》 第三讲 三维空间刚体运动