Opencv学习——仿射变换和透视变换

仿射变换是一种二维坐标之间的变换，变换前后保持图形的平直性和平行性。仿射变换可以理解为是向量经过一次线性变换和一次平移变换。
透视变换可以看做是二维与三维坐标之间的变换，变换前后没有了仿射变换的特性。其实仿射变换是透视变换的一种特殊形式。下图能够展示两种变换的区别：

---

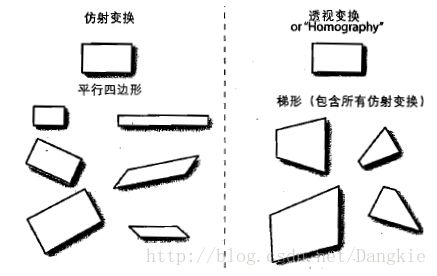
仿射变换

仿射变换可以表示为一个线性变换加上一个平移变换，所以仿射变换可以用来表示：
a. 旋转（线性变换）
b. 平移（向量加）
c. 缩放操作（线性变换）

---

通常用2X3矩阵表示仿射变换

A=[a0a2a1a3]2X2

B=[b0b1]2X1

M=[AB]=[a0a2a1a3b0b1]2X3

求仿射变换矩阵需要知道变换前后三组对应点的位置。

---

Opencv中有封装好的仿射变换函数：

void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

参数InputArray src：输入变换前图像

参数OutputArray dst：输出变换后图像，需要初始化一个空矩阵用来保存结果，不用设定矩阵尺寸

参数InputArray M：变换矩阵，用另一个函数getAffineTransform()计算

参数Size dsize：设置输出图像大小

参数int flags=INTER_LINEAR：设置插值方式，默认方式为线性插值

---

生成变换矩阵的函数getAffineTransform():

Mat getAffineTransform(const Point2f* src, const Point2f* dst)

参数const Point2f* src：原图的三个固定顶点

参数const Point2f* dst：目标图像的三个固定顶点

返回值：Mat型变换矩阵，可直接用于warpAffine()函数

注意，顶点数组长度超过3个，则会自动以前3个为变换顶点；数组可用Point2f[]或Point2f*表示

---

透视变换

透视变换是将图像投影到一个新的视平面，也称作投影映射。透视变换能提供更大的灵活性，但是一个透视投影并不是线性变换，因此其采用的是3X3的映射矩阵，控制点变为4个。
透视变换矩阵如下：

⎡⎣⎢a11a21a31a12a22a32a13a23a33⎤⎦⎥3X3

其中

[a11a21a12a22]2X2

表示线性变换，比如比例变换、剪切变换、旋转变换。
[a31a32] 表示平移
[a13a23]T 产生透视变换。可以看到，仿射变换是透视变换的特殊形式。

---

Opencv中透视变换的函数为：

void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

生成变换矩阵的函数为：

Mat getPerspectiveTransform(const Point2f* src, const Point2f* dst)

---

实例代码

Mat AffineTrans(Mat src, Point2f* scrPts, Point2f* dstPts)
{
    Mat dst;
    Mat Trans = getAffineTransform(scrPts, dstPts);
    warpAffine(src, dst, Trans, Size(src.cols, src.rows), CV_INTER_CUBIC);
    return dst;
}

Mat AffineTrans(Mat src, Point2f* scrPts, Point2f* dstPts)
{
    Mat dst;
    Mat Trans = getAffineTransform(scrPts, dstPts);
    warpAffine(src, dst, Trans, Size(src.cols, src.rows), CV_INTER_CUBIC);
    return dst;
}

int main()
{
    Mat I = imread("..//img.jpg");  //700*438

    Point2f srcPts[4] = { Point2f(100, 50), Point2f(100, 390), Point2f(600, 50), Point2f(600, 390) };
    Point2f dstPts[4] = { Point2f(200, 100), Point2f(200, 330), Point2f(500, 50), Point2f(600, 390) };
    Mat dst_affine = AffineTrans(I, srcPts, dstPts);
    Mat dst_perspective = PerspectiveTrans(I, srcPts, dstPts);

    for (int i = 0; i < 4; i++)
    {
        circle(I, srcPts[i], 2, Scalar(0, 0, 255), 2);
        circle(dst_affine, dstPts[i], 2, Scalar(0, 0, 255), 2);
        circle(dst_perspective, dstPts[i], 2, Scalar(0, 0, 255), 2);
    }

    imshow("origin", I);
    imshow("affine", dst_affine);
    imshow("perspective", dst_perspective);
    waitKey();
    return 0;
}