- 牛客算法竞赛入门笔记1
wuhudaduizhang
牛客笔记动态规划算法1024程序员节
2021-10-20:昨天开的新坑,看了前几集感觉还可以,后悔为什么没早点跟着学,以前就感觉到了自己的知识体系太散了,这个课好像是11月还是12月结束,她说能达到icpc铜牌水平,我姑且相信好吧,希望跟着学完能有点进步,不求铜牌,cf先能上个1500吧呜呜呜。#模拟,枚举与贪心字符串(nowcoder.com)尺取法(说实话这可能是我第一次见到这个做法,或者第一次知道它的学名),正常暴力想法应该是
- 每日一道算法题 成绩排序
BraveOxCow
算法python开发语言
题目成绩排序_牛客题霸_牛客网(nowcoder.com)Pythonn=int(input())flag=int(input())ans=[]for_inrange(n):name,score=input().split('')ans.append([name,int(score)])ans.sort(key=lambdax:x[1],reverse=notflag)foreinans:prin
- 计算机视觉目标检测-DETR网络
next_travel
计算机视觉目标检测人工智能
目录摘要abstractDETR目标检测网络详解二分图匹配和损失函数DETR总结总结摘要DETR(DEtectionTRansformer)是由FacebookAI提出的一种基于Transformer架构的端到端目标检测方法。它通过将目标检测建模为集合预测问题,摒弃了锚框设计和非极大值抑制(NMS)等复杂后处理步骤。DETR使用卷积神经网络提取图像特征,并将其通过位置编码转换为输入序列,送入Tra
- 题解 | #字符统计#hashmap + treeset
2301_79125642
java
双非简历求拷打,秋招够用吗#我的简历长这样##最后再改一次简历#async/await的用途和工作原理async/await是ES8(ES2017)引入的一种用于处理异步操作的语法,它建立在ProVue中组件传值的方式Vue中组件传值的方式主要有以下几种:https://www.nowcoder.com/issue异步编程?异步编程是一种编程模式,用于处理可能会花费较长时间的操作,而不会阻塞其他代
- NC01--股票(一次交易)、合并k个有序链表、字符串的排列、接雨水问题、输出二叉树的右视图
minastinis of king
#牛客网高频50题
1、股票(一次交易)https://www.nowcoder.com/practice/64b4262d4e6d4f6181cd45446a5821ec?tpId=117&&tqId=37717&rp=1&ru=/activity/oj&qru=/ta/job-code-high/question-ranking根本用不上什么动态规划,直接遍历数组,然后找到最低价格,然后在后面减去最低价格,得到利
- HJ17.坐标移动
蓝色的simon
python华为机试python面试
HJ17.坐标移动https://www.nowcoder.com/practice/119bcca3befb405fbe58abe9c532eb29描述开发一个坐标计算工具,A表示向左移动,D表示向右移动,W表示向上移动,S表示向下移动。从(0,0)点开始移动,从输入字符串里面读取一些坐标,并将最终输入结果输出到输出文件里面。输入:合法坐标为A(或者D或者W或者S)+数字(两位以内)坐标之间以;
- NowCoder HJ17 坐标移动
红毛乌龟
算法刷题c++数据结构算法NowCoder
前言华为机试刷题题目:HJ17坐标移动编程语言:C++解题状态:基础不牢,磕磕绊绊的思路本题主要是模拟题,分为三个步骤:获取字符串后利用分号获取坐标移动步骤;判断步骤是否合法;移动坐标。代码#include#include#include#includeusingnamespacestd;boolisValid(string&s){if(s.size()3)returnfalse;if(s[0]!
- 纯干货!字节跳动 100 篇精选面经集锦(建议收藏分享)
技术小羊
java面试
首发于公众号:互金运营狗作为字节Top10内推人,有越来越多的同学经过我内推杀入了字节面试环节,为了帮助大家更好的备战面试,我从牛客网筛选、整理了100篇精选真实面经,覆盖技术、产品、运营、HR等各个岗位。机会永远属于有准备的人,强烈建议你收藏分享本文,并认真阅读文中的精选面经!更多面经,可以打开牛客网https://www.nowcoder.com/interview/center进行筛选,查看
- 每日一题2024年8月30日
Gin387
算法
E-不知道叫什么名字_2023年广东工业大学腾讯杯新生程序设计竞赛(nowcoder.com)大致思路:题目要求选择连续的,男女人数相等的。题目给出男生为1,女生为0,这里猜测要把女生的0改成-1(猜测,不知道对不对)通过一些手段,前缀和+map,发现可以完美解决这个问题。#includeusingnamespacestd;typedeflonglongll;typedefdoubledb;typ
- 2024牛客寒假算法基础集训营2 G Tokitsukaze and Power Battle (easy)
Jiu-yuan
算法
原题链接:https://ac.nowcoder.com/acm/contest/67742/G题目大意:一段长为n的数组,可以进行二种操作,第一种是改变其中的一个数,第二种是给定一个区间[l,r],可以选择这个区间中的一段[i,j],可以在这一段里面选择一个分割点x,[i,x]的区间和减去[x+1,j]的区间和为y,当进行这个操作的时候,题目要求找出最大的y。思路:进行第二种操作的时候,可以贪心
- 河南萌新联赛2024第(三)场:河南大学
osir.
c++
K-暴食之史莱姆_河南萌新联赛2024第(三)场:河南大学(nowcoder.com)思路:注意到,当史莱姆的邻居体积比自己大时,可以使邻居吃掉其他史莱姆来使邻居体积缩小,再被史莱姆吃掉那么,通过观察容易得到。在只考虑左侧史莱姆的情况,编号为i的史莱姆能吃掉的同伴个数,一定是左边第一个比i体积小的史莱姆所能吃的数量。右侧同理。由于史莱姆可以优先选择左右中较大者吃,且吃的条件为大于等于,所以答案就是
- 华为OD机试真题-勾股数元组-2024年OD统一考试(官方D卷原题)
「已注销」
华为od
介绍2024年OD统一考试(D卷),最新题库。5-11月份考试都是从本专栏中抽题,命中率百分之95。多语言解法,在线练习机试是在牛客考试,练习的时候也可以在牛客网练习,提前熟悉操作https://ac.nowcoder.com/acm/contest/5652/K点击上方链接进入牛客练习界面,可以自定义题目,自定义输入、输出等等,华为OD真实机试环境,非其他第三方平台模拟。D卷总目录不清楚D卷有多
- 牛客刷题|HJ24 合唱队,HJ25 数据分类处理 , HJ26 字符串排序
Huiwen_Z
笔试刷题数据结构算法python牛客
HJ24合唱队题目链接:合唱队_牛客题霸_牛客网(nowcoder.com)思路:对队列中每个元素分别找左边最长递增序列和右边最长递减序列(都不一定是连续的),那么以当前元素为“山顶”可以保留的最大人数就是两者之和减一。寻找最长递增序列可以用动态规划实现。但测试用例只通过了2/20,我使用其它用户发的代码并作了些格式上的修改,依然只能通过2/20。有没有人能告诉为什么:(代码(未通过所有测试案例)
- 牛客刷题 | HJ45 名字的漂亮度,HJ48 从单向链表中删除指定值的节点
Huiwen_Z
笔试刷题python开发语言
HJ45名字的漂亮度题目链接:名字的漂亮度_牛客题霸_牛客网(nowcoder.com)思路:统计单词中每个字母出现的次数,依次按出现频率从大到小分配漂亮度。代码importsysn=int(sys.stdin.readline().strip())strings=[]foriinrange(n):strings.append(sys.stdin.readline().strip())defbea
- 《剑指offer》78--把二叉树打印成多行[C++][Java]
贫道绝缘子
剑指offer算法散列表leetcode
把二叉树打印成多行_牛客题霸_牛客网【牛客题霸】收集各企业高频校招笔面试题目,配有官方题解,在线进行百度阿里腾讯网易等互联网名企笔试面试模拟考试练习,和牛人一起讨论经典试题,全面提升你的技术能力https://www.nowcoder.com/practice/445c44d982d04483b04a54f298796288?tpId=13&tags=&title=&difficulty=0&ju
- 字符串字符数的统计之chart_length()
慕.晨风
MYSQL总结mysql
语法char_length(string)注意:char_length()统计的是字符串中字符的个数length()统计的是字符串的字节数栗子对过长的昵称截取处理_牛客题霸_牛客网(nowcoder.com)描述现有用户信息表user_info(uid用户ID,nick_name昵称,achievement成就值,level等级,job职业方向,register_time注册时间):iduidni
- mysql 输出所在月份的最后一天
慕.晨风
mysqlandroid数据库
内置函数LAST_DAY(date)参数:date:一个日期或日期时间类型的值,表示要获取所在月份最后一天的日期。返回值:返回一个日期值,表示输入日期所在月份的最后一天。栗子月总刷题数和日均刷题数_牛客题霸_牛客网(nowcoder.com)请从中统计出2021年每个月里用户的月总刷题数month_q_cnt和日均刷题数avg_day_q_cnt(按月份升序排序)以及该年的总体情况,示例数据输出如
- CSS图片背景样式
沃和莱特
前端csscss3html
前言上次我们介绍的CSS的背景样式,但是图片背景样式我们没有过多阐述,那么CSS的图片背景样式还有哪些值得一看的地方呢,一起看看叭~在学习过程中总觉得基础巩固不好,那有可能就是理论没有得到很好的实践,亲自将代码实现出来才能更容易掌握所学,比如刷题就是一个很好的选择,边学边练,学完即练!牛客网https://www.nowcoder.com/exam/oj?page=1&tab=HTML/CSS&t
- 牛客竞赛-新手上路-语法入门-选择结构.c
傲寒439
c语言
F吃瓜群众链接:https://ac.nowcoder.com/acm/contest/19304/F来源:牛客网题目描述群众想要吃瓜,于是给你一个瓜让你切,但是作为考验告诉你西瓜的重量,问你能否将这个西瓜分成两部分,每个部分都是偶数。注意:这里说的是能否分成两部分,不是能否平均分成两部分输入描述:输入一行,包含一个整数weight,表示西瓜的重量1intmain(){intweight;scan
- 2024春晚纸牌魔术原理----环形链表的约瑟夫问题
一枕眠秋雨>o<
数据结构与算法题集链表数据结构
一.题目及剖析https://www.nowcoder.com/practice/41c399fdb6004b31a6cbb047c641ed8a?tab=note这道题涉及到数学原理,有一般公式,但我们先不用公式,看看如何用链表模拟出这一过程二.思路引入思路很简单,就试创建一个单向循环链表,然后模拟报数,删去对应的节点三.代码引入/***代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方
- 链表的回文结构
一枕眠秋雨>o<
数据结构与算法题集链表数据结构
一.题目及剖析https://www.nowcoder.com/practice/d281619e4b3e4a60a2cc66ea32855bfa?tab=note众所周知,如果这道题的链表改为数组,这道题将十分简单,用左右指针就行,但人家说的是链表,显然左右指针是行不通的.二.思路引入1.找到链表的中间节点,将其分为两部分2.将后半部分反转3.如果反转后value与前半部分一样,则是回文结构而前
- 【C基础刷题】第九讲
睡觉待开机
C语言初阶基础刷题c语言开发语言
本系列博客为个人刷题思路分享,有需要借鉴即可。1.目录大纲:2.题目链接:统计成绩00:00:00⸺00:09:00题号:BC33链接:https://www.nowcoder.com/practice/cad8d946adf64ab3b17a555d68dc0bba?tpId=290&tqId=39821&ru=/exam/oj密码验证00:09:00⸺00:15:11题号:(⽆)链接:http
- 倒计时55天
算法怎么那么难啊
c++
(0条未读通知)牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ(nowcoder.com)a.#includeusingnamespacestd;#defineintlonglongconstintN=2e5+6;constintinf=0x3f3f3f3f;voidsolve(){intn,cn1=0,cn2=0;strings,str1="dfs",st
- C语言学习记录
曾浩轩
C语言学习记录学习c语言
牛牛的字符矩形_牛客题霸_牛客网(nowcoder.com)#includeintmain(){chara;//定义要输入的字符scanf("%c",&a);//输入字符for(inti=3;i>0;i--)//由题可知要输出3*3的矩阵,则每行内容相同,相当于循环三次,则用for语句{//注意for语句的格式,中间是分号,不是逗号,刚开始不清楚限定范围可以一步步推一下,后面就熟悉了printf(
- C语言学习记录
曾浩轩
C语言学习记录学习c语言
牛牛的字符菱形_牛客题霸_牛客网(nowcoder.com)#includeintmain(){chara;scanf("%c",&a);printf("%c\n",a);printf("%c%c%c\n",a,a,a);printf("%c%c%c%c%c\n",a,a,a,a,a);printf("%c%c%c\n",a,a,a);printf("%c\n",a);return0;}记得加换行
- C语言学习记录
曾浩轩
C语言学习记录学习
牛牛学说话之-整数_牛客题霸_牛客网(nowcoder.com)本篇总结:因为要输入一个数,所以要先定义一个数,才能输入。又因为要输入的数为整数,所以用int来定义,a为要输入这个数的名字。scanf格式:scanf("%d",&a);和printf区分一下,printf("%d",a);先记住哪个要&,哪个不要&,后面应该会学到为什么这块一个要一个不要再先记住,整数为%d,后面其它类型的变量就是
- 牛客寒假算法基础集训营4-J-Applese 的减肥计划
Honyelchak
算法刷题c++
链接:https://ac.nowcoder.com/acm/contest/330/J来源:牛客网已知Applese两只手分别产生的力的大小,以及它们之间的夹角,试求两力合力的大小。输入描述:仅一行三个整数f1,f2,af1,f2,a,分别表示两只手产生的力的大小以及它们之间的夹角。输出描述:输出一个实数表示两力合力的大小,要求相对误差或绝对误差不超过10−610−6。严格来讲,如果你的答案是a
- 2023牛客寒假算法基础集训营4 J-清楚姐姐学排序
awaqqq
算法
原题链接:J-清楚姐姐学排序_2023牛客寒假算法基础集训营4(nowcoder.com)思路:一道表面说排序,实际上是建图的题,根据输入的条件同时建立一个正向和反向的图,用dfs分别搜索,复杂度为n2,不过该题的nusingnamespacestd;intmain(){inti,j,k,n,m;inta[1005][1005]={0},ans[1005];scanf("%d%d",&n,&m);
- C语言学习记录
曾浩轩
C语言学习记录学习c语言
小飞机_牛客题霸_牛客网(nowcoder.com)飞机翅膀12个*,第一行按5下空格,再按两下*,再按5下空格,最后一行按4下空格,再按一下*,再按两下空格,再按一下*,再按4下空格数格子就完了,本篇还是练格式。
- 2018暑期牛客多校第七场 J-Sudoku Subrectangles
余西子
牛客
链接:https://www.nowcoder.com/acm/contest/145/J来源:牛客网SudokuSubrectangles时间限制:C/C++1秒,其他语言2秒空间限制:C/C++32768K,其他语言65536KSpecialJudge,64bitIOFormat:%lld题目描述Youhavean*mgridofcharacters,whereeachcharacterisa
- 面向对象面向过程
3213213333332132
java
面向对象:把要完成的一件事,通过对象间的协作实现。
面向过程:把要完成的一件事,通过循序依次调用各个模块实现。
我把大象装进冰箱这件事为例,用面向对象和面向过程实现,都是用java代码完成。
1、面向对象
package bigDemo.ObjectOriented;
/**
* 大象类
*
* @Description
* @author FuJian
- Java Hotspot: Remove the Permanent Generation
bookjovi
HotSpot
openjdk上关于hotspot将移除永久带的描述非常详细,http://openjdk.java.net/jeps/122
JEP 122: Remove the Permanent Generation
Author Jon Masamitsu
Organization Oracle
Created 2010/8/15
Updated 2011/
- 正则表达式向前查找向后查找,环绕或零宽断言
dcj3sjt126com
正则表达式
向前查找和向后查找
1. 向前查找:根据要匹配的字符序列后面存在一个特定的字符序列(肯定式向前查找)或不存在一个特定的序列(否定式向前查找)来决定是否匹配。.NET将向前查找称之为零宽度向前查找断言。
对于向前查找,出现在指定项之后的字符序列不会被正则表达式引擎返回。
2. 向后查找:一个要匹配的字符序列前面有或者没有指定的
- BaseDao
171815164
seda
import java.sql.Connection;
import java.sql.DriverManager;
import java.sql.SQLException;
import java.sql.PreparedStatement;
import java.sql.ResultSet;
public class BaseDao {
public Conn
- Ant标签详解--Java命令
g21121
Java命令
这一篇主要介绍与java相关标签的使用 终于开始重头戏了,Java部分是我们关注的重点也是项目中用处最多的部分。
1
- [简单]代码片段_电梯数字排列
53873039oycg
代码
今天看电梯数字排列是9 18 26这样呈倒N排列的,写了个类似的打印例子,如下:
import java.util.Arrays;
public class 电梯数字排列_S3_Test {
public static void main(S
- Hessian原理
云端月影
hessian原理
Hessian 原理分析
一. 远程通讯协议的基本原理
网络通信需要做的就是将流从一台计算机传输到另外一台计算机,基于传输协议和网络 IO 来实现,其中传输协议比较出名的有 http 、 tcp 、 udp 等等, http 、 tcp 、 udp 都是在基于 Socket 概念上为某类应用场景而扩展出的传输协
- 区分Activity的四种加载模式----以及Intent的setFlags
aijuans
android
在多Activity开发中,有可能是自己应用之间的Activity跳转,或者夹带其他应用的可复用Activity。可能会希望跳转到原来某个Activity实例,而不是产生大量重复的Activity。
这需要为Activity配置特定的加载模式,而不是使用默认的加载模式。 加载模式分类及在哪里配置
Activity有四种加载模式:
standard
singleTop
- hibernate几个核心API及其查询分析
antonyup_2006
html.netHibernatexml配置管理
(一) org.hibernate.cfg.Configuration类
读取配置文件并创建唯一的SessionFactory对象.(一般,程序初始化hibernate时创建.)
Configuration co
- PL/SQL的流程控制
百合不是茶
oraclePL/SQL编程循环控制
PL/SQL也是一门高级语言,所以流程控制是必须要有的,oracle数据库的pl/sql比sqlserver数据库要难,很多pl/sql中有的sqlserver里面没有
流程控制;
分支语句 if 条件 then 结果 else 结果 end if ;
条件语句 case when 条件 then 结果;
循环语句 loop
- 强大的Mockito测试框架
bijian1013
mockito单元测试
一.自动生成Mock类 在需要Mock的属性上标记@Mock注解,然后@RunWith中配置Mockito的TestRunner或者在setUp()方法中显示调用MockitoAnnotations.initMocks(this);生成Mock类即可。二.自动注入Mock类到被测试类 &nbs
- 精通Oracle10编程SQL(11)开发子程序
bijian1013
oracle数据库plsql
/*
*开发子程序
*/
--子程序目是指被命名的PL/SQL块,这种块可以带有参数,可以在不同应用程序中多次调用
--PL/SQL有两种类型的子程序:过程和函数
--开发过程
--建立过程:不带任何参数
CREATE OR REPLACE PROCEDURE out_time
IS
BEGIN
DBMS_OUTPUT.put_line(systimestamp);
E
- 【EhCache一】EhCache版Hello World
bit1129
Hello world
本篇是EhCache系列的第一篇,总体介绍使用EhCache缓存进行CRUD的API的基本使用,更细节的内容包括EhCache源代码和设计、实现原理在接下来的文章中进行介绍
环境准备
1.新建Maven项目
2.添加EhCache的Maven依赖
<dependency>
<groupId>ne
- 学习EJB3基础知识笔记
白糖_
beanHibernatejbosswebserviceejb
最近项目进入系统测试阶段,全赖袁大虾领导有力,保持一周零bug记录,这也让自己腾出不少时间补充知识。花了两天时间把“传智播客EJB3.0”看完了,EJB基本的知识也有些了解,在这记录下EJB的部分知识,以供自己以后复习使用。
EJB是sun的服务器端组件模型,最大的用处是部署分布式应用程序。EJB (Enterprise JavaBean)是J2EE的一部分,定义了一个用于开发基
- angular.bootstrap
boyitech
AngularJSAngularJS APIangular中文api
angular.bootstrap
描述:
手动初始化angular。
这个函数会自动检测创建的module有没有被加载多次,如果有则会在浏览器的控制台打出警告日志,并且不会再次加载。这样可以避免在程序运行过程中许多奇怪的问题发生。
使用方法: angular .
- java-谷歌面试题-给定一个固定长度的数组,将递增整数序列写入这个数组。当写到数组尾部时,返回数组开始重新写,并覆盖先前写过的数
bylijinnan
java
public class SearchInShiftedArray {
/**
* 题目:给定一个固定长度的数组,将递增整数序列写入这个数组。当写到数组尾部时,返回数组开始重新写,并覆盖先前写过的数。
* 请在这个特殊数组中找出给定的整数。
* 解答:
* 其实就是“旋转数组”。旋转数组的最小元素见http://bylijinnan.iteye.com/bl
- 天使还是魔鬼?都是我们制造
ducklsl
生活教育情感
----------------------------剧透请原谅,有兴趣的朋友可以自己看看电影,互相讨论哦!!!
从厦门回来的动车上,无意中瞟到了书中推荐的几部关于儿童的电影。当然,这几部电影可能会另大家失望,并不是类似小鬼当家的电影,而是关于“坏小孩”的电影!
自己挑了两部先看了看,但是发现看完之后,心里久久不能平
- [机器智能与生物]研究生物智能的问题
comsci
生物
我想,人的神经网络和苍蝇的神经网络,并没有本质的区别...就是大规模拓扑系统和中小规模拓扑分析的区别....
但是,如果去研究活体人类的神经网络和脑系统,可能会受到一些法律和道德方面的限制,而且研究结果也不一定可靠,那么希望从事生物神经网络研究的朋友,不如把
- 获取Android Device的信息
dai_lm
android
String phoneInfo = "PRODUCT: " + android.os.Build.PRODUCT;
phoneInfo += ", CPU_ABI: " + android.os.Build.CPU_ABI;
phoneInfo += ", TAGS: " + android.os.Build.TAGS;
ph
- 最佳字符串匹配算法(Damerau-Levenshtein距离算法)的Java实现
datamachine
java算法字符串匹配
原文:http://www.javacodegeeks.com/2013/11/java-implementation-of-optimal-string-alignment.html------------------------------------------------------------------------------------------------------------
- 小学5年级英语单词背诵第一课
dcj3sjt126com
englishword
long 长的
show 给...看,出示
mouth 口,嘴
write 写
use 用,使用
take 拿,带来
hand 手
clever 聪明的
often 经常
wash 洗
slow 慢的
house 房子
water 水
clean 清洁的
supper 晚餐
out 在外
face 脸,
- macvim的使用实战
dcj3sjt126com
macvim
macvim用的是mac里面的vim, 只不过是一个GUI的APP, 相当于一个壳
1. 下载macvim
https://code.google.com/p/macvim/
2. 了解macvim
:h vim的使用帮助信息
:h macvim
- java二分法查找
蕃薯耀
java二分法查找二分法java二分法
java二分法查找
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年6月23日 11:40:03 星期二
http:/
- Spring Cache注解+Memcached
hanqunfeng
springmemcached
Spring3.1 Cache注解
依赖jar包:
<!-- simple-spring-memcached -->
<dependency>
<groupId>com.google.code.simple-spring-memcached</groupId>
<artifactId>simple-s
- apache commons io包快速入门
jackyrong
apache commons
原文参考
http://www.javacodegeeks.com/2014/10/apache-commons-io-tutorial.html
Apache Commons IO 包绝对是好东西,地址在http://commons.apache.org/proper/commons-io/,下面用例子分别介绍:
1) 工具类
2
- 如何学习编程
lampcy
java编程C++c
首先,我想说一下学习思想.学编程其实跟网络游戏有着类似的效果.开始的时候,你会对那些代码,函数等产生很大的兴趣,尤其是刚接触编程的人,刚学习第一种语言的人.可是,当你一步步深入的时候,你会发现你没有了以前那种斗志.就好象你在玩韩国泡菜网游似的,玩到一定程度,每天就是练级练级,完全是一个想冲到高级别的意志力在支持着你.而学编程就更难了,学了两个月后,总是觉得你好象全都学会了,却又什么都做不了,又没有
- 架构师之spring-----spring3.0新特性的bean加载控制@DependsOn和@Lazy
nannan408
Spring3
1.前言。
如题。
2.描述。
@DependsOn用于强制初始化其他Bean。可以修饰Bean类或方法,使用该Annotation时可以指定一个字符串数组作为参数,每个数组元素对应于一个强制初始化的Bean。
@DependsOn({"steelAxe","abc"})
@Comp
- Spring4+quartz2的配置和代码方式调度
Everyday都不同
代码配置spring4quartz2.x定时任务
前言:这些天简直被quartz虐哭。。因为quartz 2.x版本相比quartz1.x版本的API改动太多,所以,只好自己去查阅底层API……
quartz定时任务必须搞清楚几个概念:
JobDetail——处理类
Trigger——触发器,指定触发时间,必须要有JobDetail属性,即触发对象
Scheduler——调度器,组织处理类和触发器,配置方式一般只需指定触发
- Hibernate入门
tntxia
Hibernate
前言
使用面向对象的语言和关系型的数据库,开发起来很繁琐,费时。由于现在流行的数据库都不面向对象。Hibernate 是一个Java的ORM(Object/Relational Mapping)解决方案。
Hibernte不仅关心把Java对象对应到数据库的表中,而且提供了请求和检索的方法。简化了手工进行JDBC操作的流程。
如
- Math类
xiaoxing598
Math
一、Java中的数字(Math)类是final类,不可继承。
1、常数 PI:double圆周率 E:double自然对数
2、截取(注意方法的返回类型) double ceil(double d) 返回不小于d的最小整数 double floor(double d) 返回不大于d的整最大数 int round(float f) 返回四舍五入后的整数 long round
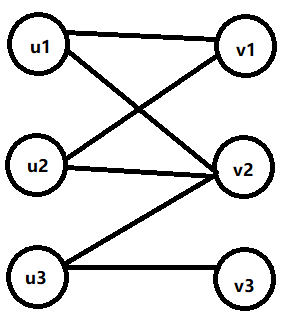 图一
图一
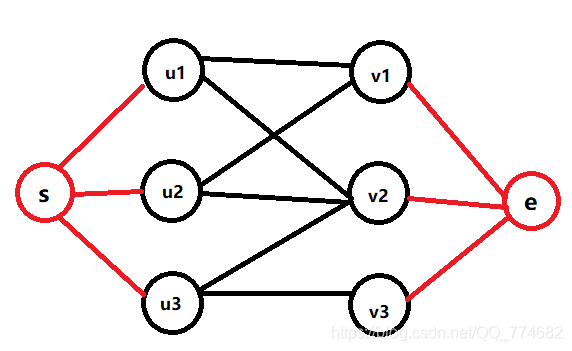 图二
图二