PAT甲 7-4 Cartesian Tree (30分) 两种解法

7-4 Cartesian Tree (30分)

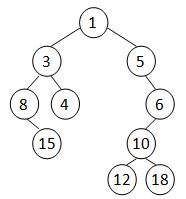
A Cartesian tree is a binary tree constructed from a sequence of distinct numbers. The tree is heap-ordered, and an inorder traversal returns the original sequence. For example, given the sequence { 8, 15, 3, 4, 1, 5, 12, 10, 18, 6 }, the min-heap Cartesian tree is shown by the figure.

Your job is to output the level-order traversal sequence of the min-heap Cartesian tree.

Input Specification:

Each input file contains one test case. Each case starts from giving a positive integer N (≤30), and then N distinct numbers in the next line, separated by a space. All the numbers are in the range of int.

Output Specification:

For each test case, print in a line the level-order traversal sequence of the min-heap Cartesian tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

10
8 15 3 4 1 5 12 10 18 6

Sample Output:

1 3 5 8 4 6 15 10 12 18

思路：

利用最小堆的性质，根为当前子树最小的值，得到根的下标，而中序遍历为LNR，得到根下标即可分开左子树和右子树。
方法一：建树+BFS即可，详见代码。
方法二：不必建树，在遍历得到根节点的同时记录树深度，并将各层节点存入深度数字level[ ]， 之后从遍历0~最深层依次输出即可。

Code（方法一）:

#include 
#include 
#include 
#include

Code(方法二)：

#include 
#include 
#include 
#include
using namespace std;
const int INF = 0x3fffffff;
const int maxn = 210;
struct node{
	int data;
	node* lchild,*rchild;
	node(int x){
		data = x; lchild = rchild = NULL;
	}
};
vector in;
int find_min(int L,int R){
	int Min = INF,index = -1;
	for(int i = L; i <= R; i++){
		if(in[i] < Min){
			Min = in[i];
			index = i; 
		}
	}
	return index;
}
int MaxH = -1;
vector level[maxn];
void build(int L,int R,int height){
	if(L > R) return ;
	if(height > MaxH) MaxH = height;
	int X = find_min(L,R);
	level[height].push_back(in[X]);
	build(L,X-1,height+1);
	build(X+1,R,height+1);
}
int cnt = 0,n;
int main(){
	scanf("%d",&n);
	in.resize(n);
	for(int i = 0; i < n; i++)
		 scanf("%d",&in[i]);
	build(0,n-1,0);
	for(int i = 0; i <= MaxH; i++){
		if(i == 0){
			printf("%d",level[i][0]);
		}
		else {
			for(int j = 0; j < level[i].size();j++)
				printf(" %d",level[i][j]);
		}
	}
	printf("\n");
	return 0;
}