用卡尔曼滤波处理轨迹

卡尔曼滤波这个词老是听到，一直也没有耐心看，最近准备看看轨迹挖掘相关的东西，第一步轨迹处理中卡尔曼滤波就又出现了，终于耐着性子研究了两天(一看一堆矩阵就脑壳痛），期间网上找了不少代码和博客，算是大概明白了，还自己改了一版代码，做个小笔记

卡尔曼滤波这个东西，我理解下来就是一方面通过理论模型算出一个预测值，另一方面通过测量手段测出一个测量值，然后通过加权平均得出一个估计值，使得这个估计值最接近真实值。

原理的详细推导可以详细见卡尔曼滤波：从入门到精通或Understanding the Basis of the Kalman Filter via a Simple and Intuitive Derivation [Lecture Notes]

这里先记一下算法步骤
$${\hat{X}}_k^{-}代表预测值,{\hat{Z}}_k代表测量值，{\hat{X}}_k代表估计值，X_k代表真实值$$

• step1

用t-1时刻的估计值通过理论模型得到t时刻的预测值
$${\hat{X}}_k^{-}=F_{k-1}{\hat{X}}_{k-1}^{-}+B_{k-1}{u}_{k-1}$$
更新此时的真实vs预测误差的协方差矩阵
$$P_k^{-}=F_{k-1}{P}_{k-1}{F}_{k-1}^T+Q$$

• step2

计算卡尔曼增益
$$K_k=P_k^{-}{H}^T(H{P}_k^{-}1H^T+R{)}^{-1}$$
融合预测值和测量值，更新t时刻的估计值
$${\hat{X}}_k={\hat{X}}_k^{-}+K_k({\hat{Z}}_k-H{\hat{X}}_k^{-})$$

• step3

更新此时的真实vs估计误差的协方差矩阵
$$P_k=(I-K_{k}H)P_k^{-}$$

下面简单理解一下其中关键步骤是两个协方差矩阵的更新
第一个真实vs预测误差的协方差矩阵
构建的理论模型为
$$X_k=F_{k-1}{X}_{k-1}+B_k{u}_k+w_k,w_k代表高斯噪声,均值为0，协方差矩阵为Q$$
在执行更新预测值时，实际是 ${\hat{X}}_t^{-}=F_t{\hat{X}}_{t-1}+B_t{u}_t$
则根据矩阵性质，$P_k^{-}=F_{k-1}{P}_{k-1}{F}_{k-1}^T$，同时还要考虑$w_t$ ,
所以$P_k^{-}=F_{k-1}{P}_{k-1}{F}_{k-1}^T+Q$

可以看到预测更新实际上相当于对不确定性做“加法”：将当前状态转换到下一时刻（并增加一定不确定性即$A_t$的影响），再把外界的干扰（建模因素之外的影响，比如突然一阵风）叠加上去（又增加了一点不确定性即$Q$）。

图1 真实vs预测误差的协方差矩阵更新，图片来自[1]

另一个是真实vs估计误差的协方差矩阵

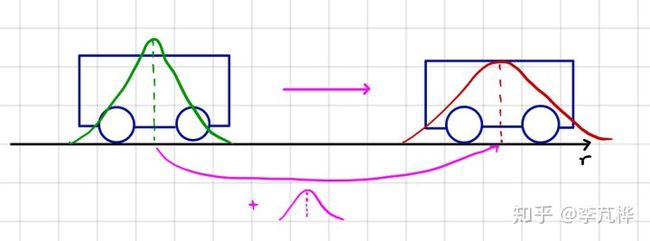
图2 预测值分布和测量值分布的融合，图片来自 [2]

在一维这个融合，就是两个高斯分布的乘法，而两个高斯分布的乘积仍然是高斯分布
以下公式均来自 [2]


则以上两个高斯分布做乘法后融合成的高斯分布为，如图2所示，绿色即为新的高斯分布

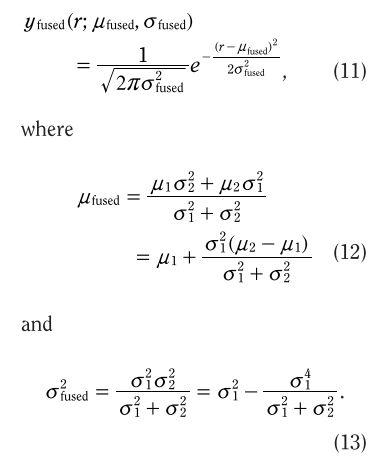
引入$H$矩阵和高维后，就出来以下的一般形式


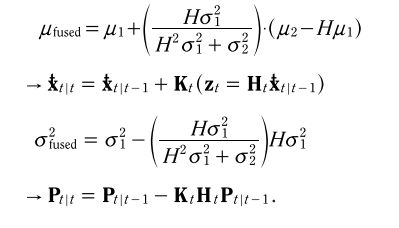
$K_k$（卡尔曼增益）代表测量值的权重，$K_k$越大，代表测量值在估计值计算中比重越大

---

kalman滤波处理轨迹实例代码，代码是根据 [3] 的基础上改的，改动的地方是状态变量$X$加入了二维坐标和速度。

# -*- coding: utf-8 -*-
__author__ = 'fff_zrx'
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from decimal import Decimal
import geopandas
from shapely import geometry
import pyproj
import re

class KalmanFilter(object):
    def __init__(self,F,H,gps_var,pre_var):
        self.F =F # 预测时的矩阵
        self.H = H # 测量时的矩阵
        self.n=self.F.shape[0]
        self.Q = np.zeros((self.n,self.n))
        self.Q[2,2]=pre_var
        self.Q[3,3]=pre_var
        self.R = np.zeros((n,n))
        self.R[0,0]=gps_var
        self.R[1,1]=gps_var
        self.R[2,2]=gps_var
        self.R[3,3]=gps_var
        self.P = np.eye(self.n)
        self.B = np.zeros((self.n, 1))
        self.state=0

    #第一次传入时设置观测值为初始估计值
    def set_state(self,x,y,time_stamp):
        self.X = np.zeros((self.n, 1))
        self.speed_x=0
        self.speed_y=0
        self.X=np.array([[x],[y],[self.speed_x],[self.speed_y]])
        self.pre_X=self.X
        self.time_stamp=time_stamp
        self.duration=0

    def process(self,x,y,time_stamp):
        if self.state==0:
            self.set_state(x,y,time_stamp)
            self.state=1
            return x,y

        self.duration=(time_stamp-self.time_stamp).seconds
        self.time_stamp=time_stamp
        self.Z=np.array([[x],[y],[self.speed_x],[self.speed_y]])
        #更新时长
        self.F[0,2]=self.duration
        self.F[1,3]=self.duration
        self.predict()
        self.update()
        return self.X[0,0],self.X[1,0]


    # 预测
    def predict(self, u = 0):
        # 实现公式x(k|k-1)=F(k-1)x(k-1)+B(k-1)u(k-1)
        # np.dot(F,x)用于实现矩阵乘法
        self.X = np.dot(self.F, self.X) + np.dot(self.B, u)
        # 实现公式P(k|k-1)=F(k-1)P(k-1)F(k-1)^T+Q(k-1)
        self.P = np.dot(np.dot(self.F, self.P), self.F.T) + self.Q


    # 状态更新,使用观测校正预测
    def update(self):
        # 新息公式y(k)=z(k)-H(k)x(k|k-1)
        y = self.Z - np.dot(self.H, self.X)
        # 新息的协方差S(k)=H(k)P(k|k-1)H(k)^T+R(k)
        S = self.R + np.dot(self.H, np.dot(self.P, self.H.T))
        # 卡尔曼增益K=P(k|k-1)H(k)^TS(k)^-1
        # linalg.inv(S)用于求S矩阵的逆
        K = np.dot(np.dot(self.P, self.H.T), np.linalg.inv(S))
        # 状态更新，实现x(k)=x(k|k-1)+Ky(k)
        self.X = self.X + np.dot(K, y)
        #计算速度
        self.speed_x=(self.X[0,0]-self.pre_X[0,0])/self.duration
        self.speed_y=(self.X[1,0]-self.pre_X[1,0])/self.duration
        self.pre_X=self.X
        print(self.X)
        # 定义单位阵
        I = np.eye(self.n)
        # 估计值vs真实值 协方差更新
        # P(k)=[I-KH(k)]P(k|k-1)
        self.P = np.dot(I - np.dot(K, self.H), self.P)


data=pd.read_table(r'E:\data\Taxi数据\T-drive Taxi Trajectories\release\taxi_log_2008_by_id\12.txt',delimiter=',',header=None)
data.columns=['id','time','lon','lat']
data['time']=pd.to_datetime(data['time'])
data=data.sort_values(by='time')
data=data.reset_index()
data.columns=['label','id','time','lon','lat']
data=data.drop_duplicates(subset="time")
data['lon']= data['lon'].astype(float)
data['lat']= data['lat'].astype(float)

# -------中位数法-------
n=4
data1=data[['lon','lat']].rolling(n,min_periods=1,axis=0).median()
data=pd.concat([data[['label','id','time']],data1],axis=1)
data['geometry']=data.apply(lambda x: geometry.Point(x.lon,x.lat),axis=1)
data=geopandas.GeoDataFrame(data)
data.crs = pyproj.CRS.from_user_input('EPSG:4326')
data=data.to_crs(crs="EPSG:2385")
data['geometry']=data['geometry'].astype(str)
data['x']=data['geometry'].apply(lambda x: float(re.findall(r'POINT \((.*?) ',x)[0]))
data['y']=data['geometry'].apply(lambda x: float(re.findall(r'\d (.*?)\)',x)[0]))
data.to_csv(r'C:\Users\fff507\Desktop\before.csv',index=False)


# ------卡尔曼滤波------
# 状态变量的个数,x,y,speed_x,speed_y
n=4
F = np.eye(n)
H = np.eye(n)
# 速度噪声的方差
pre_var=15**2
# 坐标测量噪声的方差
gps_var=100**2
gps_kalman=KalmanFilter(F=F,H=H,gps_var=gps_var,pre_var=pre_var)
lon_list=[]
lat_list=[]
for index,row in data.iterrows():
    lon,lat=gps_kalman.process(x=row['x'],y=row['y'],time_stamp=row['time'])
    lon_list.append(lon)
    lat_list.append(lat)
print(lon_list)
data['new_lon']=lon_list
data['new_lat']=lat_list
data['geometry']=data.apply(lambda x:geometry.Point(x.new_lon,x.new_lat),axis=1)
data=geopandas.GeoDataFrame(data)
data.crs = pyproj.CRS.from_user_input('EPSG:2385')
data=data.to_crs(crs="EPSG:4326")
data['geometry']=data['geometry'].astype(str)
data['new_lon']=data['geometry'].apply(lambda x: float(re.findall(r'POINT \((.*?) ',x)[0]))
data['new_lat']=data['geometry'].apply(lambda x: float(re.findall(r'\d (.*?)\)',x)[0]))
fig= plt.figure(figsize=(8,4),dpi=200)
ax1 = fig.add_subplot(111)
ax1.plot(data['lon'],data['lat'],'-*',label='before')
ax1.plot(data['new_lon'],data['new_lat'],'-o',label='after',alpha=0.5)
plt.show()
data.to_csv(r'C:\Users\fff507\Desktop\after.csv',index=False)

参考资料：

[1]卡尔曼滤波：从入门到精通
[2]Understanding the Basis of the Kalman Filter via a Simple and Intuitive Derivation [Lecture Notes] R. Faragher. Signal Processing Magazine, IEEE , vol.29, no.5, pp.128-132, Sept. 2012 doi: 10.1109/MSP.2012.2203621
[3]卡尔曼滤波理解与实现