写在前面---
现在我们学习凸包的有关算法（终于开始凸包的学习了）。也算是初步接触计算几何了。
凸包的概念是在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包，表示为：
在二维空间中，凸包也可以形象的理解为最小的包含所有点的凸多边形。
X的凸包可以用X=（x1,x2,x3,...,x12）的线性组合来构造，即：![S=\{\sum_{j=1}^{n}t_jx_j|x_j\in X,\sum_{j=1}^nt_j=1,t_j\in[0,1]\}](http://img.e-com-net.com/image/info8/0a3c6835f133441788251222c4ef1229.gif)
在计算几何中，凸包问题是一类比较常见的问题，不仅在计算机程序设计竞赛中，在统计等现实问题中也有着广泛的应用。
现在已经证明了凸包算法的时间复杂度下界是O(n*logn),但是当凸包的顶点数h也被考虑，Krik-patrick和Seidel的剪枝搜索算法可以达到O(n*logh)，在渐进意义下达到最优。最常用的凸包算法是Graham扫描法和Jarvis步进法。本章主要学习Graham扫描法，其正确性的证明和Jarvis步进法可以参考《算法导论》
卷包裹法
原理：
卷包裹法的原理比较简单：先找一个最边缘的点（一般位于最下方，如果有多个点，则选择最左方的点），假设有一条绳子，以该点为端点向右边逆时针旋转直到碰到另一个点为止，此时找出凸包的一条边；然后再用新找到的点作为端点，继续旋转绳子，找到下一个端点；重复这一步骤直至围成一个凸多边形，即可得到这个点集的凸包。卷包裹法的时间复杂度为O（n^2）。
步骤：
Step1：选择点集中最下面的点，如果有多个，则选择最下面的点中最左边的一个，所选择的点是凸包的第一个点。
Step2：以水平向右的方向作为初始射线方向，逆时针旋转，选择第一条在初始射线之上的射线作为当前射线，当前射线经过凸包的第二个点。
Step3：以当前射线为基准，继续逆时针旋转找到最靠近该射线的一条射线，从而找到凸包的另一个点。把这条射线作为当前射线，这个过程一直继续，直至回到第一个点。
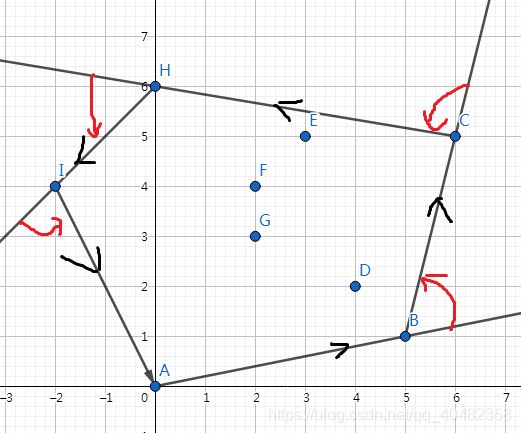大概的过程就是这个图所示了（灵魂画图）
对于旋转射线这个操作，当然不能真的旋转，我们可以用以下几种方法来实现：
A.把每条射线与其他n-2条射线比较，每步的效率是O（n^2）。
B.通过计算各射线与射线AB的夹角的方式，效率为O（n），但由于计算夹角存在浮点运算，会导致浮点误差。
C.直接使用叉积运算求各条射线斜率的相对关系，从而得到另一条射线，效率是O（n），不存在浮点误差。
哪个方法好一目了然，所以你选择C项，并将其所对应的答题卡涂成黑色。
如果出现寻找的射线上有多个点的时候，一般只是用和保留距离当前端点最远的哪一点。
实现：
看起来似乎挺简单的，实现一下也不难：
写一个板子，输入n个点，然后输出它的凸包的边长。
这个代码和样例模拟的就是上面说的步骤了：
首先得到最下面的点，发现有多个最下面的点，得到最左边的。
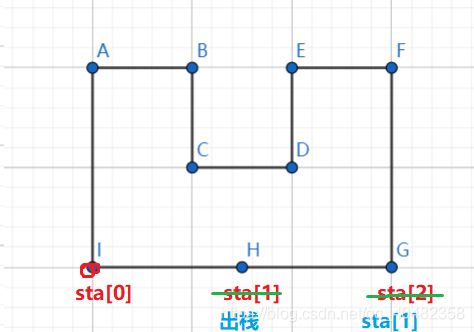三点入栈，然后判断是否严格左转。发现不是，H出栈。
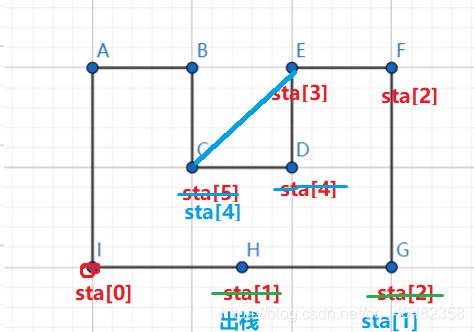如图所示，后面的正常入栈，直到C点的时候，发现不是严格左转，所以D点出栈，凸包变成了如图所示，连接CE点。
再找到B点，发现又不是严格左转，C出栈，判断E，E出栈，判断F，GFE构成严格左转，B入栈。凸包变成了IGFB.
剩下的就是还是一步步的走，然后判断即可。
最后得出的凸包为LGFAL。
Code：
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
还有一个写法，选择一个必定在凸包上的一个点，然后以该点为中心维护上凸壳和下凸壳。
说一下思路：这种写法是重复遍历两次，每次从1~n点的顺时针，然后是从n~1点的顺时针。sort的时候也只用按坐标排序即可。
这个方法与上面的方法类似，但是可能可以用在其他方面，比如只用得到半个凸壳的题目：https://blog.csdn.net/qq_40482358/article/details/88826317
Code：
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
