luogu P3379 【模板】最近公共祖先（LCA）

lca最近公共祖先，是指两个点最近的祖先节点；求lca我知道的有三种倍增，
st表，tarjan,我要介绍的是倍增，我才不会告诉你我只会这一个。
话说我学lca可真的路途曲折，在qbxt，lcy dalao 的vector存图让我这个没接触过stl的蒟蒻完全懵圈，夏令营没有讲，学校里学长讲我又完美错过，心里的痛说不出，，，
还好又找学长单独开了下小灶，额，跑偏了，回归正题。
最近公共祖先的话，貌似挺有用，因为之前多次看到这个字眼（毕竟我只是刚刚打过模板的蒟蒻，题的话还没有去接触），其实我都快放弃lca了，但是学长突然留了一道题需要用lca，，，虽然我还是没有打出来。。。有跑偏了
最近公共祖先，首先我们可以很容易想到，先从一个点往上找它的祖先节点，然后标记下，再找另外一个点的祖先节点，找到的第一个标记的点就是两点的最近公共祖先，但当树退化成链时，复杂度会变为O（N）,这样的话,显然是不行的，所以我们在这个基础上利用倍增的思想优化一下，一个一个的跳，有点慢，那我们就两个两个的跳，在此之前先将两个点提到同一深度，然后用倍增的思想，同时往上跳2^n步，这样的复杂度可以优化到O(logn)。
总结一下倍增求lca就以下几点：
1.先确定两个节点的高低，即先假设一个节点在下面，如果不是交换两个节点，使假设的节点确实下面；
2.将两点提至同一深度；
3.两点同时往上跳，直至跳到最近公共祖先；

下面是luogu的模板题 附代码+注释

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入输出格式

输入格式：

第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。

接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。

输出格式：

输出包含M行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例

输入样例#1： 复制

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
输出样例#1： 复制
4
4
1
4
4

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

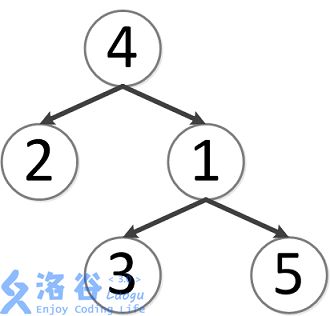
该树结构如下：

第一次询问：2、4的最近公共祖先，故为4。

第二次询问：3、2的最近公共祖先，故为4。

第三次询问：3、5的最近公共祖先，故为1。

第四次询问：1、2的最近公共祖先，故为4。

第五次询问：4、5的最近公共祖先，故为4。

故输出依次为4、4、1、4、4。

#include
#include
#include
#include
#include

using namespace std;
int n;
int m;
int s;
int x,y;
int a,b;
int p;

const int maxn = 5211314;
const int inf = 500521;

int head[maxn];
int f[inf][20];//f[a][b]意思为a点往上面跳2^b步到达的祖先节点
int deep[maxn];//用来存点的深度
struct edge{//结构体存边
    int from;
    int to;
    int next;
}e[maxn];
inline int read(){//读入优化
    int x = 0;int f = 1;char c = getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f = -f;
        c = getchar();
    }
    while(c<='9'&&c>='0'){
        x = x*10+c-'0';
        c= getchar();
    }
    return x*f;
}

void add(int a,int b){//邻接表存边
    p++;
    e[p].from = head[a];
    e[p].to = b;
    head[a] = p;
}
void dfs(int root){//dfs深搜建树
    for(int i = head[root]; i ; i = e[i].from)
    {
        if(!deep[e[i].to]){
            deep[e[i].to] = deep[root] + 1;
            f[e[i].to][0] = root;
            dfs(e[i].to);
        }
    }
}
int lca(int x,int y){
    if(deep[x] < deep[y]){//确定两点深度
        x^=y^=x^=y;//异或操作交换x,y两点的值
    }
//将两点提至同一深度
    for(int i = 19; i>=0; i--){//这里的19根据数据范围而定
        if(deep[f[x][i]]>=deep[y]){//这点很重要deep值越大说明深度值越大在下面，
            x = f[x][i];//我一开始想不明白的原因就是没想通这里
        }
    }
    if(x == y)return x;//如果y是x的祖先节点或者x是y的祖先节点

    for(int i = 10; i>=0; i--){//让两点同时往上跳
        if(f[x][i] != f[y][i]){//如果相等说明已经是或者在最近公共祖先之上了
            x = f[x][i];//两点不断接近最近公共祖先
            y = f[y][i];//最终一定能到达最近公共祖先的儿子节点
        }
    }
    return f[x][0];//因为是儿子节点所以需要在往上跳一步
}
int main(){
    n = read();
    m = read();
    s = read();
    for(int i = 1; i<=n-1; i++){
        x = read();
        y = read();
        add(x,y);
        add(y,x);
    }
    deep[s] = 1;
    f[s][0] = s;
    dfs(s);
    for(int i = 1; i<=19; i++){
        for(int j = 1; j<=n; j++){
            f[j][i] = f[f[j][i-1]][i-1];
        }
    }
    for(int i = 1; i<=m; i++){
        a = read();
        b = read();
        printf("%d\n",lca(a,b));
    }
    return 0;
} 

转载于:https://www.cnblogs.com/Euplectella/p/9907297.html