T1 帽子戏法
问题描述
小 Y 有一个\(n*n*n\)的“帽子立方体” ,即一个\(n\)层的立方体,每层的帽子都
可以排成\(n*n\)的矩阵。 “帽子立方体”中的每一个帽子都有一个颜色,颜色共 26
种,用 26 个大写字母来表示。
现在,小 Y 邀请小 F 来表演她的帽子戏法。小 F 会 \(2\) 种帽子戏法:
- 指定一个长方体形状的区域,将指定区域内的所有帽子全部变成指定的
颜色。 指定一个长方体形状的区域,将指定区域内所有指定颜色帽子全部变成
绿色(用大写字母\(G\)表示) 。
小Y很喜欢绿色, 所以初始时立方体内的所有帽子都是绿色的。 不仅如此,
小Y还会时不时地提出问题:他会指定一个长方体形状的区域,并询问在这个
区域内有多少绿色的帽子。
小Y的帽子琳琅满目,请你来帮他数一数吧!输入格式
第一行 2 个正整数\(n,Q\),分别描述立方体的大小、以及小 F 表演帽子戏法和
小 Y 提问的总次数。
接下来Q行,每行第一个数\(op(0 ≤ op ≤ 2)\)表示这次询问或帽子戏法的类型。
若\(op = 0\),表示这是小 Y 的一个提问,接下来 6 个正整数描述询问指定的
区域。
若\(op = 1\),接下来 6 个正整数表示帽子戏法指定的区域,之后一个大写字母
/%0表示小 F 会把指定区域内的所有帽子都变成\(col\)颜色。
若\(op = 2\), 接下来 6 个正整数表示帽子戏法指定的区域, 表示小 F 会把指定
区域内的所有帽子都变成绿色。
描述一个区域的方法为:用 6 个整数\(x_0,y_0,z_0,x_1,y_1,z_1\) 表示从第\(x_0\)层至第\(x_1\)
层,从第\(y_0\)行至第\(y_1\)行,从第\(z_0\)列至第\(z_1\)列的区域(层、行、列编号的范围都是
1…n) 。输出格式
对于每个询问,输出一行一个整数表示答案。
样例
样例输入 3 5 1 2 2 2 3 3 3 B 1 1 3 2 3 3 2 R 0 1 1 1 3 3 3 2 3 3 3 3 3 3 B 0 2 1 3 3 3 3
| 样例输出 |
|---|
| 18 |
| 3 |
数据范围
对于 10%的数据,保证\(n=1\)。
对于另外 10%的数据,保证只有询问操作,即保证\(op=0\)。
对于 30%的数据,保证\(n≤ 5,Q ≤ 10\)。
对于 100%的数据,保证\(n ≤ 40,Q ≤ 200\)。
题解
看一下数据范围就应该知道是暴力的吧。\(maxn*maxn*maxn*maxQ=12800000\),排除每一次查询、更改操作全部为最大操作的情况可知,\(O(n^3)\)可解
贴出代码
#include
#define maxn 405
using namespace std;
int n,q,ans;
int x1,z1,x2,y2,z2;
int y01,cmd;
char cas;
char a[maxn][maxn][maxn];
int main(){
//freopen("hat.in","r",stdin);
//freopen("hat.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>q;
for(register int i=0;i<=n;i++){
for(register int j=0;j<=n;j++){
for(register int k=0;k<=n;k++)a[i][j][k]='G';
}
}
while(q--){
cin>>cmd;
if(cmd==0){
ans=0;
cin>>x1>>y01>>z1>>x2>>y2>>z2;
//cout<>x1>>y01>>z1>>x2>>y2>>z2;
//cout<>cas;
for(register int i=x1;i<=x2;i++){
for(register int j=y01;j<=y2;j++){
for(register int k=z1;k<=z2;k++){
a[i][j][k]=cas;
}
}
}
}
else if(cmd==2){
cin>>x1>>y01>>z1>>x2>>y2>>z2;
//cout<>cas;
for(register int i=x1;i<=x2;i++){
for(register int j=y01;j<=y2;j++){
for(register int k=z1;k<=z2;k++){
if(a[i][j][k]==cas){
a[i][j][k]='G';
//cout< T2 最大队列
问题描述
给定一个长度为\(n\)的排列(共包含\(n\)个整数,每个数取值范围\(1\)和\(n\)之间,且每个正整数出现并只出现一次)。借助一个栈,依次将这个排列的每个元素进栈,并在合适的时候出栈,可以得到不同的出栈序列。不同的操作会带来不同的出栈序列,请你求出在所有可能的方案中,字典序最大的出栈序列。
输入格式
输入数据共包括两行。
第一行包含一个正整数\(n\),表示给定的排列的长度。
第二行包含\(n\)个正整数,描述给定的序列。
输出格式
仅一行,共\(n\)个整数,表示你计算出的出栈序列。
样例
| 样例输入1 |
|---|
| 4 |
| 4 2 1 3 |
| 样例输出1 |
|---|
| 4 3 1 2 |
| 样例输入2 |
|---|
| 10 |
| 4 5 1 2 6 10 7 8 3 9 |
| 样例输出2 |
|---|
| 10 9 3 8 7 6 2 1 5 4 |
数据范围
题解
先说说自己的错误思路。先将所有数据排序,然后为了让字典序尽量大则每次选取当前没有被选取的最大值。同时我们维护一个上一次选取的数的位置\(lastp\),若\(lastp\)的值比当前我们要出栈的元素的位置的值要小我们则直接让当前元素出栈,否则我们从将\(lastp\)到当前位置\(i\)的所有元素全部出栈。在一定程度上这样的思路是正确的,但是我们如果这样做就考虑漏了一种情况,即当我们先输出元素比我们从\(lastp\)输出到\(i\)时中间值的字典序要小,则整体字典序会比正确答案偏小。
上40分代码
#include
#define maxn 200005
using namespace std;
inline int read(){
register char c=get();register int f=1,_=0;
while(c>'9' || c<'0')f=(c=='-')?-1:1,c=get();
while(c<='9' && c>='0')_=(_<<3)+(_<<1)+(c^48),c=get();
return _*f;
}
int n;
int a[maxn];
struct edge{
int a;
int flag;
}E[maxn];
bool cmp(edge a,edge b){
if(a.a!=b.a)return a.a>b.a;
return a.flag save;
int lastp=-1;
int out[maxn],note=1;
//map jump;
int main(){
freopen("seq.in","r",stdin);
freopen("seq.out","w",stdout);
n=read();
//cout<=E[i].flag;j--){
if(save.count(a[j]))continue;
out[note]=a[j];
note++;
save.insert(a[j]);
//jump[j]=max(jump[j],lastp-1);
}
lastp=E[i].flag;
}
}
for(register int i=1;i 事实上,为了将上述情况纳入考虑范围内,我们选择使用在线的算法。我们令当前栈顶的元素为\(x\),并使所有还没有入栈的元素中的最大值\(y\)。当\(x\le y\)时我们不断入栈,直到情况不满足为止。此时则将y直接扔出去即可。当没有比栈顶元素更大的值时我们就不再入栈,而一直弹出栈顶元素直到满足条件或没有元素位置。由于每次查询最大值时的复杂度为\(O(n)\),遍历一次的复杂度为\(O(n)\),总复杂度则为\(O(n^2)\)。
朴素\(O(n^2)\)代码如下
#include
#define maxn 200005
using namespace std;
inline char get(){
static char buf[30],*p1=buf,*p2=buf;
return p1==p2 && (p2=(p1=buf)+fread(buf,1,30,stdin),p1==p2)?EOF:*p1++;
}
inline int read(){
register char c=get();register int f=1,_=0;
while(c>'9' || c<'0')f=(c=='-')?-1:1,c=get();
while(c<='9' && c>='0')_=(_<<3)+(_<<1)+(c^48),c=get();
return _*f;
}
int n;
int a[maxn];
int maxnow;
int getmax(int now){
int cas=-1;
for(register int i=now;i<=n;i++)cas=max(cas,a[i]);
return cas;
}
stack box;
int out[maxn],note=1;
int main(){
//freopen("1.txt","r",stdin);
n=read();
for(register int i=1;i<=n;i++)a[i]=read();
for(register int i=1;i<=n;i++){
//cout<=maxnow){
out[note]=box.top();
//cout< 当然朴素算法并不能满足\(n=200000\)等大数据的要求,因此我们要对算法进行优化。事实上我们可以减少取最大值的次数——我们只在开始时和每一次最大值被pop出栈时才重新取一次最大值
for(register int i=1;i<=n;i++)a[i]=read(),maxnow=max(maxnow,a[i]);
for(register int i=1;i<=n;i++){
if(i==1){
box.push(a[i]);
continue;
}
if(box.top()>=maxnow){
maxnow=getmax(i);
out[note]=box.top();
box.pop();
note++;
i--;
continue;
}
box.push(a[i]);
}完整代码
#include
#define maxn 200005
using namespace std;
inline char get(){
static char buf[30],*p1=buf,*p2=buf;
return p1==p2 && (p2=(p1=buf)+fread(buf,1,30,stdin),p1==p2)?EOF:*p1++;
}
inline int read(){
register char c=get();register int f=1,_=0;
while(c>'9' || c<'0')f=(c=='-')?-1:1,c=get();
while(c<='9' && c>='0')_=(_<<3)+(_<<1)+(c^48),c=get();
return _*f;
}
int n;
int a[maxn];
int maxnow;
int getmax(int now){
int cas=-1;
for(register int i=now;i<=n;i++)cas=max(cas,a[i]);
return cas;
}
stack box;
int out[maxn],note=1;
int main(){
//freopen("1.txt","r",stdin);
n=read();
for(register int i=1;i<=n;i++)a[i]=read(),maxnow=max(maxnow,a[i]);
for(register int i=1;i<=n;i++){
if(box.empty()){
box.push(a[i]);
continue;
}
if(box.top()>=maxnow){
maxnow=getmax(i);
out[note]=box.top();
//cout< T3 思考熊的马拉松
题面描述
今年,\(n\)只思考熊参加了校园马拉松比赛。马拉松的赛道是环形的,每圈的
长度是:,完成比赛需要跑;圈。
比赛中,甲领先乙很长距离,绕过一圈或多圈后从后面追上了乙的现象叫做
“套圈” 。 套圈现象非常常见, 例如: 跑得比谁都快的\(S\)熊可以套某些熊 \(L-1\)圈;
\(U\) 熊经常进行日常耐力训练,套圈次数和被套圈次数基本持平;而$ M$ 作为一只
老年熊,则是被套\(L-1\)圈的那种。
与人不同的是, 思考熊在跑步时都是匀速运动。$ W$ 熊是这次比赛的计时员,
他统计了参赛的\(n\)只熊的速度\(v_1 ,v_2 ,…,v_n\)(其中最大的一个是\(S\)熊的速度) 。现
在\(W\)熊希望你告诉他,当速度最快的\(S\)熊到达终点时,场上所有熊中总共发生
了多少次套圈现象。
注意:在\(S\)熊刚刚到达终点那一刻,如果甲恰好追上了乙,此时也算作甲将
乙套圈。
输入格式
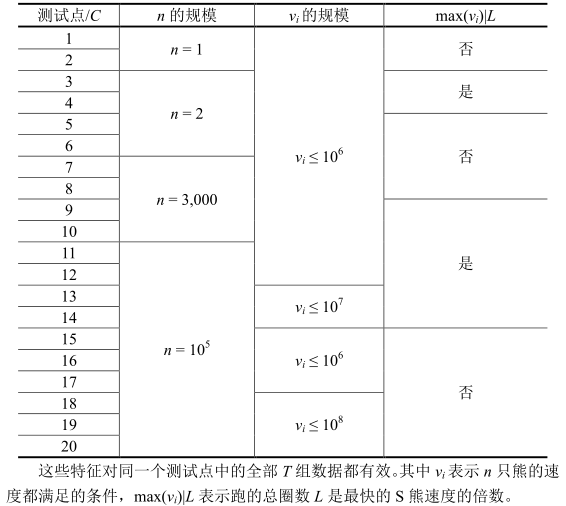
输入的第一行包含两个整数\(T,C\),分别表示这个测试点的组数和这个测试点的编号。对于测试数据,保证\(T=10\)。
每组数据的第一行包含3个正整数\(n,A,L\),分别表示思考熊的只数、跑道每圈的长度和完成比赛所需要的圈数。保证\(A,L\le 10^8\)。
第二行包含\(n\)个正整数\(v_1,v_2,...,v_n\)表示每只思考熊的速度。保证这些数互不相同。
输出格式
输出\(T\)行,分别表示每组数据中所有熊发生的套圈总次数。
样例
| 样例输入 |
|---|
| 1 0 |
| 3 2 6 |
| 1 2 3 |
| 样例输出 |
|---|
| 8 |
数据范围
题解
这是一道数学题,去隔壁请一个数竞大佬来吧。
首先我们已知比赛结束时间\(t_{end}\)一定是\(\frac{L*A}{v_{max}}\),则此时为了求出结束时间我们就先将所有熊的速度从大到小排序,然后求\(t_{end}=\frac{A*L}{v_1}\)即可知道能跑的最长时间。这时我们知道对于$ \forall v_1
\(<\) v_2 \(都一定有\) v_2 $ 套 $ v_1 k 圈的时间是$ t_k=\frac{Ak}{v_2-v_1} \(,则我们可以取\) t_k\le t_{end} \(为答案。则因此联立方程组后可知,对于我们排序后的数列中\) \forall v_i和v_j \(,一定有\) a_{ij}=\frac{Aabs(v_i-v_j)}{v_{end}} \(。我们枚举每一个数即可得到答案。复杂度即为\)O(n^2)$。
** 虽然$ \forall v $$ 都 $ \le 10^8 \(,但是\) \forall x=abs(v_1-v_2)L \(不一定满足\) x \subseteq (1,10^8) $ !
贴出该题的部分分解法(50)**
#include
#define maxn 100005
using namespace std;
inline char get(){
static char buf[30],*p1=buf,*p2=buf;
return p1==p2 && (p2=(p1=buf)+fread(buf,1,30,stdin),p1==p2)?EOF:*p1++;
}
inline long long read(){
register char c=get();register long long f=1,_=0;
while(c>'9' || c<'0')f=(c=='-')?-1:1,c=get();
while(c<='9' && c>='0')_=(_<<3)+(_<<1)+(c^48),c=get();
return _*f;
}
long long n,A,L;
long long v[maxn];
bool cmp(long long a,long long b){
return a>b;
}
long long ans=0;
int main(){
//freopen("2.txt","r",stdin);
long long T,C;
T=read();C=read();
//cout<<1< #include
using namespace std;
typedef long long int64;
const int MAXN = 100005;
int n;
int64 L,A;
int64 a[MAXN], b[MAXN], c[MAXN];
inline int lowbit(int x) {
return x & (-x);
}
void insert(int x) {
for (int i = x; i <= n; i += lowbit(i)) c[i]++;
}
int getsum(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i];
return res;
}
int main() {
//freopen ("running.in","r",stdin);
//freopen ("running.out","w",stdout);
int T, case_num;
scanf("%d%d", &T, &case_num);
while (T--) {
scanf("%d%lld%lld", &n, &A, &L);
int64 ans = 0;
int64 maxv = 0;
for (int i = 1; i <= n; i++) {
c[i] = 0;
scanf("%lld", &a[i]);
maxv = max(maxv, a[i]);
a[i] *= L;
}
sort(a + 1, a + n + 1);
reverse(a + 1, a + n + 1);
for (int i = 1; i <= n; i++) {
ans += (a[i] / maxv) * (int64) (n - 2 * i + 1);
a[i] %= maxv;
}
for (int i = 1; i <= n; i++) b[i] = a[i];
sort(b + 1, b + n + 1);
int m = int(unique(b + 1, b + n + 1) - (b + 1));
for (int i = 1; i <= n; i++) {
a[i] = int(lower_bound(b + 1, b + m + 1, a[i]) - b);
ans -= getsum(a[i] - 1);
insert(a[i]);
}
printf("%lld\n", ans);
}
return 0;
}