九月学习记录(数学)
已经停课这么久了,现在才开始写日记会不会晚了点……
不管怎么说,这几天的学习不是很有计划,特别是到了数学板块,每天都在划水 效率都非常低。每天还是稍微写个总结,文字或多或少。希望能坚持下去。
9.24
如上文所说,这几天都在搞数学,主要的学习资料:
-
gcp棺材铺的博客 讲台上偷的《信息学奥赛之数学一本通》- 《算法竞赛进阶指南》
上午在机房三,网卡的一批。不过反倒让我认真看了看数学(平时都看不进去)。
打了个线段树的题,发现暴力修改也能过?只是要维护区间最大值,当其为1时return,因为1不用开根。
求ax+by=c的整数解——扩欧模板(ax+by=gcd(a,b)时的一组解,求ax+by=c按c/gcd比例放大或缩小):
void euclid(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1,y=0;
gcd=a;
return;
}
euclid(b,a%b,y,x);
y-=a/b*x;
}
Luogu P1516 青蛙的约会
一看题就感觉是拓欧题目(废话么,本来就搜索的是“拓欧”标签)但刚拿起笔手玩x,y却发现并非ax+by=c的线性不定方程形式,还是得看题解……发现要对数据进行转化。
设跳了k步,当青蛙A追上B(B追上A是一样的)时,A跳的长度为km,b跳的长度为kn,跳跃距离之差为km-kn,等于二者出发点距离y-x。并且因为地球是圆的 跳的路径首尾相接且长度为L,故 km-kn=y-x(mod L)。
转换可得 (x-y)+k(m-n)=0(mod L)。因为是在模L的意义下,所以我们设 (x-y)+k(m-n)=t×L(t∈Z)
推出:
t×L+k(m-n)=(x-y)
再来对比一下
ax+by=c
L、m-n、x-y已知,而我们要求的是k。只要按照上文euclid模板打即可。
但是,我们要求他们第一次碰面,即最小的k。
当c不为gcd(a,b)的倍数时,无正整数解,直接输出“Impossible”。
这里我们需要学习,知道了一组解,如何求得全部解。直接上公式我不会证明
x’=x+k(b/gcd(a,b))
y’=y-k(a/gcd(a,b))
知道一组解x,y,可通过加减k(a/gcd(a,b))求出其他所有x’、y’。
要求最小的正整数解k(可看做x),直接通过对取模k(b/gcd(a,b))即可。
还有一点,对k(b/gcd(a,b))取模时k(b/gcd(a,b))要取绝对值。
9.25
期望在国庆前搞完数学
Luogu P3811 【模板】乘法逆元
参考zjp_shadow大佬的题解。
求解逆元的方式
- 拓展欧几里得
利用拓欧求解线性同余方程 a ∗ x ≡ c ( mod b ) 的c=1的情况。我们就可以转化为解 a * x + b * y = 1这个方程的形式。即a * x - c ≡ 0 —> a * x - c ≡ k * b
即 c = ax-kb
- 快速幂
利用费马小定理
若p为素数,a为正整数,且a、p互质。 则有a^(p-1 ) ≡ 1 ( mod p )。
即a * a ^ ( p - 2 ) = 1,故a的逆元为a ^ ( p - 2 ),用快速幂求解
- 线性算法
用于求一连串数字对于mod p的逆元。
首先知道1逆元为1。要求 i 对于模 p 的逆元,设其为 x,即 i * x = 1 (mod p)。
- 设 p =k * i + r。则 k = ⌊ p / i ⌋(向下取整),r = p % i。
- 已知 k * i + r ≡ 0 (mod p)
- 两边同乘 i -1 r -1 即 k * r -1 + i -1 ≡ 0 。
- 故 i -1≡ -k * r -1
- 又 k = ⌊ p / i ⌋,r = p % i
- 所以 i -1≡ -⌊ p / i ⌋ * (p % i)-1
注意因为要求正整数逆元,所以要去掉 -⌊ p / i ⌋ * (p % i)-1 式子的负号,直接乘上 p * (p % i)-1,变成 (p -⌊ p / i ⌋ ) * (p % i)-1 ,模 p 后结果不变。
代码
#includeLuogu P5431 【模板】乘法逆元2
我可能做了个假逆元题……
不需要挨个求出每个 a[i] 的逆元,它们不连续且值太大,不易存储。所以……
我们直接通分!
答案的分母即为所有 a[i] 值乘积。要求分子,需维护出每个数之前的 a[i] 乘积,即 pre[i] = a[1] * a[2] * ……a[i-1],和该数之后的 a[i] 乘积,即suf[i]=a[i+1] * a[i+2] * ……* a[n]。通分后的该数分子即为pre[i-1] * suf[i+1] * k^i。分母可直接求单个逆元,与线性算法思想相同,不过是用递归形式
ll inv(ll x)
{
if(x==1) return 1;
else return ((mod-mod/x)%mod*inv(mod%x)%mod)%mod;
}
完整代码:
#include乘法逆元适用于形如 a/b ≡ x (mod p)
1.线性同余方程 a ≡ bx (mod p)
2.转化为 ab-1 ≡ x (mod p)
费马小定理: p 为质数 b-1 ≡ bp-2 (mod p)
欧拉定理: b,p 互质 b-1 ≡bϕp-1 (mod p)
乘方算式:底数对p取模,指数对 φp 取模
Poj 1845 Sumdiv
约数和公式:
设 x = p1c1 * p2c2 * ……* pncn,则其约数和为
(1+p11+p12+……p1c1) * (1+p21+p12+……p2c2) *……(1+pn1+pn2+……pncn)。
发现 (1+pi1+pi2+……pici) 是等比数列,可直接用公式得出该数列和(pici+1-1) / (pi-1)。在本题中求的是ab约数和对9901取模,故每个约数的指数要乘以b,其等比数列和稍作变动即可。
需要注意的是,因为等比数列求和时要用到 pi-1 的逆元,而求逆元需要pi-1与9901互质。所以要先判断pi-1是否与9901互质,若是,则直接求逆元。若不是,则可以得到 pi%9901=1,即(1+pi1+pi2+……pici)=(1+11+12+……1ci)=ci+1。
以后要特别注意上面一点,不能直接不假思索地求逆元。而且可以根据该数的形式(如本题的pi-1)进行特判。
代码:
#include
#include 9.26
今天考试,日常爆炸……
死磕第一题,靠一个不知道什么思想的辣鸡程序得到了大众分20,第二题打了个暴力10分,第三题没来得及看……错过暴力20分。
不知为何,我的思路总是跟大家不一样不一样,经常想到什么就一直搞下去,没有什么道理和依据,也不知道用了什么思想。结果费力不讨好。下午讲解完后发现自己完全没必要这样,明明第一题的暴力思想很简单,自己却没想到——也许自己再多考虑一会儿就能想出来吧……不过放马后炮没什么意义,谁让我一直抓住一个点不放呢。第三题居然错过了暴力,考试策略太失败。
简单放一下三道题题意,没有代码因为不会正解
区间
给定一个 1 到 n 的排列 P,求有多少个由连续正整数组成的数字区间 [l,r],能用 P 中两个不相交的区间内的数字恰好拼成。两个区间内的数都要用上。
最大价值
n 个物品,每个物品有两个属性 a i ,b i,从中选出 k 个物品,并将它们排序使得价值最大,价值定义为所有选出物品的贡献。第 i 个物品被放在第 j 个位置会贡献a i · (j − 1) + b i,求 k 分别为 1,2,··· ,n 时能得到的最大价值
n ≤ 3 × 10
距离和
给定一棵 n 个点的树,树上每点有一个颜色,树上每条边长度为 1. 对于每个点,求它到所有颜色最远点的距离的和是多少
水了一天,没打题
9.27
上午写的博客没保存,心态炸了……
Luogu P4777 【模板】扩展中国剩余定理(EXCRT)
同样的,对于这个方程组
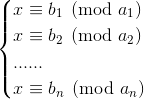
当 ai 不互质,就无法使用中国剩余定理(简称 crt),这时就需要excrt。
对于前两个方程组
x0 ≡ b1 (mod a1)
x0 ≡ b2 (mod a2)
转化为
x0 = k1 * a1 + b1
x0 = k2 * a2 + b2
联立得
k1 * a1 + b1 = k2 * a2 + b2
移项
k1 * a1 - k2 * a2 = b2 - b1
类比
ax + by = z
可用扩欧求解出k1,k2,从而推出x0的值。
已知该方程组的通解为
x = x0 + k * lcm(a1,a2)
所以原方程组
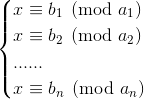
的解x与x0对于lcm(a1,a2)同余
即 x ≡ x0 (mod lcm(a1,a2))。
再将其与下面的方程组联立得到
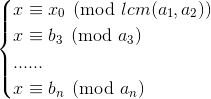
一直这样解下去直到第n次解出最终的解x。
本题运算时因为可能溢出,所以单独用了一个乘法函数,与快速幂类似理解。
#include(因为没保存,重打了一遍QAQ)
北上广深/拔山盖世算法 好吧人家叫BSGS算法,全称Baby Step,Giant Step
用于求高次同余方程中 ax ≡ b(mod p) 的x。当然《算法竞赛进阶指南》上说还有一种情况是 xa ≡ b,但这超出了我们的探讨范围,学有余力的读者可以查阅“源根”“阶”“指标”等相关资料。
设x = i * t - j (0<= j < t,0<= i <=t),
则 ai*t-j ≡ b
两边同乘 aj:ai*t = b * aj
利用哈希,以等式右边的b * aj为下标存储所有的 j,再枚举等式左边的i,计算出ai*t,哈希查找是否有先前b * aj存储的 j 值,这表明二者相等,即可用i,j,t计算出x值并退出循环。
等等,t都不知道该怎么算?好吧,其实t的值取⌈√p⌉(根号p向上取整),可以看出该算法实际运用了分块的思想。
Luogu P2485 [SDOI2011]计算器
数学综合题……开long long !
#include
{
printf("%d\n",i*t-j);
return;
}
}
printf("Orz, I cannot find x!\n");
}
int main()
{
//freopen("input.txt","r",stdin);
scanf("%lld%lld",&t,&k);
while(t--)
{
scanf("%lld%lld%lld",&a,&b,&p);
if(k==1) printf("%lld\n",qpow(a,b,p));
else if(k==2)
{
exgcd(a,p,x,y);
if(b%gcd)
{
printf("Orz, I cannot find x!\n");
continue;
}
ll mod=p/gcd;
while(x<0) x+=mod;
printf("%lld\n",((x*b/gcd)%mod+mod)%mod);
}
else if(k==3) bsgs();
}
return 0;
}
9.28
上午写的又没保存,我无fuck说
昨晚考了 Comet OJ - 模拟赛测试 Day1,不是很重视,随便打了打就干别的去了,结果连水题也没做起。其实自己正是需要这些比赛经验,以后还是要多打打oj上的比赛。
顺便说一句,我的考试排名 250二百五 似乎暗示着什么
开始搞概率期望了
216. Rainbow的信号
看了半天(“半天”可能是真的,从上午看到下午,看完题目看题解)题意都没搞明白,果真是弟弟行为。
按位计算答案。枚举二进制下的每个数位,数的大小不超过109,所以最多枚举到30位。
对每一位,枚举1到n每个数,把当前枚举的第k个数当做选取范围的右端点r,利用先前维护的值来更新答案。
设当前的枚举的数位为k,当前枚举的是第r个数,当前第r个数的数位的值为v(0或1)。
首先知道:l = r 的情况概率为 1 / n2,其他情况均为 2 / n2(因为有( l , r ) , ( r , l )两种选法,当r>l时二者交换),在加入答案时注意乘以2。
当前数位的值v为1时
因为有l = r 的情况,所以xor,and,or的答案都要加上该数位的值(若是第3数位则值为100即十进制下的4)除以n2的概率(设为pos)。
对于 or 和,l 取 r 前面的任意值,[ l, r ]的或(or)值都为1,共有(r-1)种情况,对答案 ansor 贡献(r-1)* pos。
对于 and 和,我们用 last[v]表示上个v出现的位置,只有当前数位的值为1时才能加入答案,因为如果 [ l, r ] 区间有一个值为0则and值立刻变成0了。而 l 的取值范围的数位 k 的值必须为1,这时候就需要用到 last 数组,l 可以选择的区间即为 [ last[0]+1,r ] 。
当前数位的值v为0时
对于 or 和,l 可以取的区间中的数位值必须有一个 1 ,这样异或后的值才会为一,因为last[1] 到 r 之间的数位值都是0,所以该区间不能取,可取的区间为 [1,last[1] ]。
xor 和的讨论有点麻烦,单独列出来。
对于某个数位上,1到n各个数在该数位的数位值,当前为第 r 个数:
以1为边界将区间分段,为方便理解我将它们编个号:
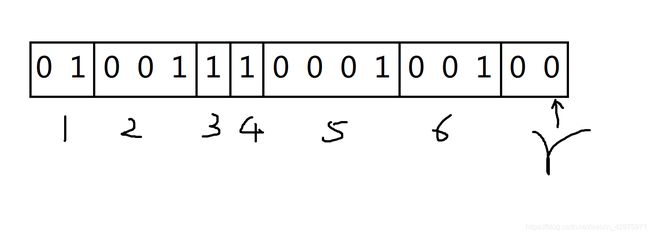
当l取1、3、5区间时,[ l , r ] 数位值的xor和为0;l取2、4、6区间时,[ l , r ] 数位值的xor和为1。
发现了吗,每个区间都只有一个1,异或0对xor和的值无影响;而每异或一次1,xor和的值就会由1变0或由0变1,所以我们用c1表示基数区间包含的值的个数,c2表示偶数区间包含的值的个数。
当前数位值为0,l 有c2个可能取值使 [ l , r ] 的xor和为1;当前数位值为1,l 有c1个可能取值使 [ l , r ] 的xor和为1。
c1,c2的维护可通过看下面的代码理解
代码:
#include今晚又考了 Comet OJ - 模拟赛测试 Day2 ,出题人竟然是暑假里给我们补过课的lch1475369大佬。
昨晚考试的 250名,仿佛隐隐预示着什么……
今晚认真答题,但……实力不够,认真也无济于事。还没考完,我就放弃治疗,来写博客了。
9.29
昨晚的考试花了太多的时间在T2上面,对字符串的处理一直是我的短板,最后还是没搞出来,指针,重载运算符,map,hash什么的一通乱搞,结果又不会调,当场gg。日常没时间打第三题。
今天把T2的暴力65分打了一下,暴枚移动方案,逐行判断单调性。
#include第二题用trie树
#include下午颓颓颓……
晚上颓颓颓……
9.30
来到成都外国语学校,开始七天补课时光 国庆七天乐 。