luogu P2014 选课

Luogu P2014 选课

第一次写博客，紧张。

传送门

题目描述

在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有N门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程a是课程b的先修课即只有学完了课程a，才能学习课程b）。一个学生要从这些课程里选择M门课程学习，问他能获得的最大学分是多少？

输入输出格式

输入格式：

第一行有两个整数N,M用空格隔开。(1<=N<=300,1<=M<=300)

接下来的N行,第I+1行包含两个整数ki和si, ki表示第I门课的直接先修课，si表示第I门课的学分。若ki=0表示没有直接先修课（1<=ki<=N, 1<=si<=20）。

输出格式：

只有一行，选M门课程的最大得分。

输入样例#1：

7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2

输出样例#1：

13

树形dp：在树的数据结构上做动态规划，通过有限次的遍历树，以求解问题。其实我动归学的一点都不好
基础题目见MZOJ1264longest、MZOJ1063士兵守卫。

• 将各课程与其先修课程用邻接表连接（双向、单向边都可以？）。所有无先修课程的科目都连上0，即0作为根节点。
• now代表当前节点；fa代表其父亲；size代表截至当前子树，总共有多少节点，并用j（
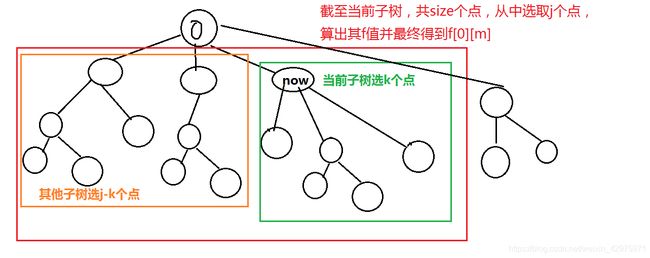
• 从（0,-1）开始dp，一个子树一个子树地求出各结点的f值。我们将整个树分为两部分，一部分为当前的子树，从中选取k个点；另一部分为其他所有遍历过的子树，从中选取j-k个点。这样依次求出各种情况的f，即f[now][j]=max(f[now][j],f[to][k]+f[now][j-k])。
• 每个点本身可以选择不学习，其子节点当然也不能学习，则不能得到相应的学分，即f[now][0]=0；若选择学习此结点，则可获得本课程的学分（w[now])，即f[now][1]=w[now]。再用相同子问题递推求出其子节点的f值。

代码：

#include
using namespace std;
#define read read()

const int maxn=305;
int n,m,cnt;
int head[maxn],w[maxn],f[maxn][maxn];

inline int read//快读
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x=x*f;
}

struct edge
{
	int v,nxt;
}e[maxn<<1];

void add(int u,int v)//邻接表
{
	e[cnt].v=v;
	e[cnt].nxt=head[u];
	head[u]=cnt++;
}

void readdata()
{
	int j;
	memset(head,-1,sizeof(head));
	n=read;m=read;m++;
	for(int i=1;i<=n;i++)
	{
		j=read;w[i]=read;
		add(i,j);
		add(j,i);
	}
}

int dp(int now,int fa)
{
	int s=0,size=1;
	f[now][0]=0;f[now][1]=w[now];
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int to=e[i].v;
		if(to==fa) continue;
		s=dp(to,now);
		size+=s;
		for(int j=size;j>0;j--)//倒序，用前面的已知数据更新后面的数据（其实我自己也还需要加强理解）
		{
			for(int k=0;k<j;k++)
			{
				if(k>s) break;
				f[now][j]=max(f[now][j],f[to][k]+f[now][j-k]);//代码核心，更新当前状态的f值
			}
		}
	}
	return size;
}

int main()
{
	//freopen("input.txt","r",stdin);
	readdata();
	dp(0,-1);
	printf("%d",f[0][m]);
	return 0;
}

敬请各位dalao斧正啊