软件构造Lab1——实验报告

1. 实验目标概述

本次实验通过求解四个问题，训练基本 Java 编程技能，能够利用 Java OO 开发基本的功能模块，能够阅读理解已有代码框架并根据功能需求补全代码，能够为所开发的代码编写基本的测试程序并完成测试，初步保证所开发代码的正确性。

另一方面，利用 Git 作为代码配置管理的工具，学会 Git 的基本使用方法。 

1. 基本的 Java OO 编程 

l 基于 Eclipse IDE 进行 Java 编程 

l 基于 JUnit 的测试 

l 基于 Git 的代码配置管理

2. 实验环境配置

2.1 简要陈述你配置本次实验所需开发、测试、运行环境的过程，必要时可以给出屏幕截图。

特别是要记录配置过程中遇到的问题和困难，以及如何解决的。

(1)下载最新eclipse安装包，并安装。

 问题：原来的eclipse无法更改工作目录。

解决：删了重新安装。

(2)JDK很早之前就配置好了，无需重新配置

(3)下载git并按步骤进行配置、初始参数的设置

 

2.2在这里给出你的GitHub Lab1仓库的URL地址（Lab1-学号）。

Lab1-1173710111:https://classroom.github.com/a/qL3Yd1XX 

 

本地开发时，本次实验只需建立一个项目，统一向 GitHub 仓库提交。实验包含的 4 个任务分别在不同的目录内开发，具体目录组织方式参见各任务最后一部分的说明。请务必遵循目录结构，以便于教师/TA 进行测试。 

 

3. 实验过程

请仔细对照实验手册，针对四个问题中的每一项任务，在下面各节中记录你的实验过程、阐述你的设计思路和问题求解思路，可辅之以示意图或关键源代码加以说明（但无需把你的源代码全部粘贴过来！）。

为了条理清晰，可根据需要在各节增加三级标题。

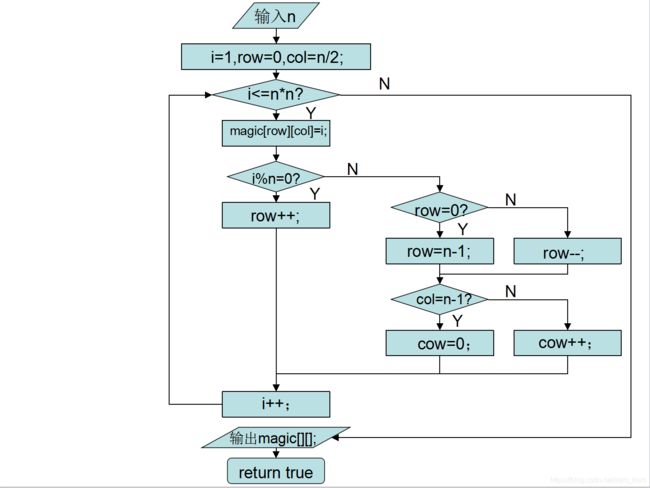
3.1 Magic Squares

A magic square of order n is an arrangement of n×n numbers, usually distinct 

integers, in a square, such that the n numbers in all rows, all columns, and both 

diagonals sum to the same constant (see Wikipedia: Magic Square)

n阶幻方是n×n数在方格中的排列，通常是独立的，使得所有行中的n个数、所有列的n个数以及两者对角线都等于同一个常数。

1. 输入文件给出一个n阶矩阵，判断该矩阵是否合法，若合法，判断是否是幻方。
2. 输入一个正整数，如果是奇数，生成一个n阶矩阵，使其满足幻方性质，并保存到输出按文件中；如果是偶数，或者不是正整数，提示输入非法。
3. 判断（2）生成的矩阵是否是幻方。

3.1.1 isLegalMagicSquare()

要求：您要编写一个Java程序（MagicSquare.java），用于检查矩阵的行/列/对角值，然后判断它是否为幻方。它返回一个布尔结果，指示输入是否是一个幻方。

实现思路：

1. 以字符串形式按行读入测试文件，文件采用相对路径；
2. 调用String.split()，对每行按”\t”分割，存到String数组中；
3. 对分割好的字符串，调用num=Integer.parseInt转化为整型变量，不能正常转化的话抛出异常，提示不满足使用”\t”分割的规则，或有非数字元素；
4. 判断是否有非正数，如果有，提示输入有非正数；
5. 输入数据处理完毕，放入二维数组中，如果判断出有不是矩阵或不是n阶矩阵的情况，抛出提示；
6. 对数组元素，求每行、每列、对角线的和，判断如果不完全相等，返回值为false，都相等则返回值为true。

3.1.2 generateMagicSquare()

 

 

把1放在第一行正中，按以下规律排列剩下的(n×n－1)个数：

（1）每一个数放在前一个数的右上一格；

（2）如果这个数所要放的格行数小于1，则放在底行，仍然要放在上一个放置的数的右一列；

（3）如果这个数所要放的格列数大于n，则放在第1列，仍然要放在上一个放置的数的上一行；

（4）如果这个数所要放的格行数小于1，且列数大于n，那么就把它放在第n行第1列；

（5）如果这个数所要放的格已经有数填入，那么就把它放在上一个放置的数的下一行同一列。

3.2Turtle Graphics

按照给定规则（forward、turn），调用给出的Turtle类、Point类，填充TurtleSoup.java中给出的各个函数，使之完成注释中给出的函数功能。

3.2.1 Problem 1: Clone and import

（1）获取代码：访问

https://github.com/rainywang/Spring2019_HITCS_SC_Lab1/tree/master/P2

下载P2文件夹，获取任务代码

1. 在本地创建git仓库：

1. 打开工作目录，右键，在当前目录打开Git Bash；
2. 输入git init 指令，将当前目录创建为本地仓库；
3. 当前目录多了一个隐藏文件夹.git，证明本地仓库已创建好了。

1. 使用git管理本地开发：

1. 和github仓库建立远程链接：访问github上的远程仓库并复制URL：

https://github.com/ComputerScienceHIT/Lab1-1173710111

1. 在本地仓库打开Git Bash，输入git remote add origin “URL”指令，建立远程链接；
2. 输入git clone “URL”指令将远程仓库的内容下载到本地仓库；
3. 将完成的项目复制到本地仓库中，输入git add .将所有文件全部加入本地仓库；
4. 输入 git commit -m “备注” 指令，将文件暂存到本地目录并且添加备注说明；
5. 输入 git push -u origin master指令，将本地仓库同步到远程仓库。

3.2.2 Problem 3: Turtle graphics and drawSquare

问题：给定爬行长度sideLength，使little turtle画一个边长为sideLength的正方形。

解决思路：（1）画正方形，就是先向前平移sideLength个单位，然后转90°，重复四遍。

（2）根据Turtle类，forward(int units) 方法的功能是向前平移units个单位；turn(double degrees) 方法是顺时针转90°

3.2.3 Problem 5: Drawing polygons

（1）public static double calculateRegularPolygonAngle(int sides)

问题：给出正整数sides（>2），返回正sides边形的内角度数。

解决思路：正sides边形内角公式：（边数-2）*180°/sides

 

（2）public static int calculatePolygonSidesFromAngle(double angle)

问题：给出浮点数angle（0

解决思路：多边形外角和=360°，所以正n边形边数公式为：sides=360/(180-angle)。

要注意浮点数与整型数据的转化，按四舍五入取整，强制转换是向下取整，精度损失较大，不满足要求。

 

（3）public static void drawRegularPolygon(Turtle turtle, int sides, int sideLength) 

问题：给出边数、边长，画一个正多边形。

解决思路：调用3.2.3.（2）的函数，求出正多边形的内角度数，然后用画正方形的方法画正多边形，只不过循环的次数改为sides次，turn的角度改为算出的角度。

 

3.2.4 Problem 6: Calculating Bearings

（1）public static double calculateBearingToPoint(double currentBearing, int currentX, int currentY, int targetX, int targetY)

问题：计算当前向量与目标向量的夹角（当前向量转过多少度后达到目标向量）。其中当前向量由当前点、当前方向决定，目标方向由当前点、目标点决定，当前方向由当前方向与竖直向上方向（y轴正方向）的夹角表示，目标向量的方向由当前点与目标点的连线与竖直向上方向（y轴正方向）的夹角表示。

解决思路：目标向量的求法如下：先求当前点与目标点的连线与y轴夹角的正切值，tan=(targetX-currentX)/(targetY-currentY)，然后调用Math库中的atan将其转化为弧度，再由公式——角度=弧度*180/PI——求得角度值，即为当前向量与y轴正方向的夹角，与currentBearing（当前方向）作差，得解。

注意，目标向量的方向和当前方向都有可能为负数，需要通过+360的方式使其转化为0-360范围内，否则在作差的时候有可能出现错误。作差的结果同样要通过——360的方式转化为正角。

 

注意要求是“当前向量转过多少度后达到目标向量”，因此必须用目标向量角度减去当前向量角度。

 

（2）public static List calculateBearings(List xCoords, List yCoords)

问题：以列表形式给出一系列点的横纵坐标。假设海龟从给出的第一点开始，面朝上(即0度)。对于其后的每一点，假设海龟在移至前一点时仍朝其所面对的方向前进。 

解决思路：对相邻两个点调用3.2.4.（1）的函数求夹角，保存在列表中，返回该列表。

 

3.2.5 Problem 7: Convex Hulls

问题：凸包问题，给出一组点的坐标，求最少的点的集合，使其他所有点都在这些点围成的闭合凸多边形内。

 

解决思路：使用gift-wrapping算法。

1. 扫描list列表，比较点的横坐标，找到横坐标最小的点作为基点left_most，并加入凸包集合中；
2. 设基点BP，中继点A，目标点B，初始化BP、A都为left_most，初始化当前方向角度为0；
3. 扫描不属于凸包集合的点作为点B，调用calculateBearingToPoint（）计算向量BP->A与向量A->B的夹角，筛选出夹角最小的点B（min_point）；
4. 令BP=A，A=B（min_point），将点B加入凸包集合中；
5. 循环（3）（4），直到新找到的点B（min_point）是初始基点left_most。

 

注意，循环终止条件的判断，是在每次计算出两向量的夹角之后，与BP->A与A->left_most的夹角比较，如果后者较小，则凸包中的点的集合已经满足条件，循环终止。

3.2.6 Problem 8: Personal art

问题：画一个图形出来。自己设计。

3.2.7 Submitting

1. 将完成的项目复制到本地仓库中，输入git add .将所有文件全部加入本地仓库；
2. 输入 git commit -m “备注” 指令，将文件暂存到本地目录并且添加备注说明；
3. 输入 git push -u origin master指令，将本地仓库同步到远程仓库。

1.  

3.3 Social Network

填充完成Person和FriendshipGraph两个类，模拟社交网络，能够实现添加节点、节点之间添加边的功能，并且可以计算两节点之间最短路。

3.3.1 设计/实现FriendshipGraph类

给出你的设计和实现思路/过程/结果。

存储结构：Set persons = new HashSet();

用HashSet存放Graph里的节点（人）。

(1) public void addVertex(Person person)

功能：将person这个节点添加到3.3.1.（1）中提到的HashSet中，相当于在图中插入一个独立的节点。

注意：要判断是否存在重名的问题，给出的要求是每个人都有自己独一无二的名字，因此插入节点前先扫描图中已存在的节点，如果有一个节点的name属性与待插入节点的name属性相同，就抛出重名提示，不插入这个节点。

(2) public void addEdge(Person p1, Person p2)

功能：在p1到p2节点之间连一条单向边。

实现：用邻接表的方式存储边，调用Person类的add_friend方法，在p1的friends集合里加入p2这个节点。

注意：为了避免重边，插入边之前先扫描p1的friends集合，判断是否有一个集合内的点，其name属性与p2相同，如果有，证明p1与p2之间已经存在这样的单向边，抛出重边提示，不插入这条边。

(3) public int getDistance(Person p1, Person p2)

功能：对给定的两个节点，求两点间的最短路。

实现：用BFS实现最短路。

1. 首先初始化图中的每个点的vis属性为false；

2. 新建一个队列，用来存放已搜索过的节点。

3. p1作为根节点，p1.vis置为true，p1加入队列；

4. 搜索p1的friends集合中未访问过的节点（vis属性为false），如果有一个满足要求的子节点等于p2，即找到一条最短路，结束搜索，返回当前路径长度distance；否则，将满足要求的子节点依次加入队列，修改其vis属性值为true；

5. 所有满足条件的子节点扫描完之后，当前路径++；

6. 取出队首节点，重复第3、4、5步操作，直到队列为空，或找到最短路径。

注意：存在p1和p2不相连的情况，这时BFS搜索到最后队列为空，扔找不到一条最短路径，因此需要在一开始设置一个标记变量flag，初始化为false，找到子节点为p2时修改flag的值为true，这样搜索结束时，如果flag的值没有发生变化，就说明两个节点不连通，返回值设为-1。

3.3.2 设计/实现Person类

1. String name：存放当前节点的名字；
2. Set friends = new HashSet()：存放以当前节点为起点的所有边的终点；
3. boolean vis：在BFS中标记当前节点是否被访问过；
4. public String name()：返回当前节点的name属性值；
5. public void add_friend(Person new_friend)：向当前节点的friends集合中添加一个新节点，即在当前节点与目标节点之间添加一条单向边；
6. public Set get_friends()：返回当前节点的friends属性；

3.3.3 设计/实现客户端代码main()

调用FriendshipGraph类的正确方法：

FriendshipGraph graph = new FriendshipGraph();

得到的graph相当于一张完整的有向图，可调用内部方法来实现节点的插入、边的插入和两点间最短路径的查询。

3.3.4 设计/实现测试用例

设计思路：（1）测试新创建的图是否为空，初始化检测；

1. 插入新节点，测试addVertex方法是否能够实现功能；
2. 插入name属性相同的节点，测试addVertex方法是否按约定抛出提示；
3. 插入新的有效边，测试addEdge方法是否能够实现功能；
4. 插入重复边，测试addEdge方法是否按约定抛出提示；
5. 选取两个连通点，测试getDistance方法是否返回正确结果；
6. 选取两个非连通点，测试getDistance方法是否返回-1；

3.4 Tweet Tweet

3.4.1 Problem 1: Extracting data from tweets

（1）public static Timespan getTimespan(List tweets)

问题：返回给出的tweets发布的时间段，即返回一个时间段，其开始时间是所有tweets发布时间最早的一个时间点，结束时间是所有tweets里发布时间最晚的一个时间点。

解决思路：如果tweets为空，返回系统当前时间点并抛出提示“no tweet included”；否则，新创建一个时间段timespan，起始时间、结束时间都初始化为第一条tweet发布的时间，然后依次扫描twees中的每条tweet，比较其发布时间与timespan的起始时间、结束时间分别进行比较，起始时间保留最早的，结束时间保留最晚的。扫描结束后，返回timespan。

（2）public static Set getMentionedUsers(List tweets)

问题：返回一个集合，集合中的元素是tweets里的text属性的字符串中的所有被@到的用户名，格式为@+用户名。

解决思路：1. 通过读注释我们知道满足要求的子串格式为@+username，其中username的规则由Tweet类的author属性的注释给出：all characters in author are drawn from {A..Z, a..z, 0..9, _, -}，由此我们可以想到用正则表达式：

"@[a-zA-Z0-9_-]*|@[a-zA-Z0-9_-]*$"来进行匹配和提取。

1. 由注释给出的规则可知，当@前面紧接着一个username的有效字符时，这个@不算被提到的用户名，因此还要单独判断匹配到的正则字符串的前一个字符是否是有效字符，如果不是，才能把当前匹配到的正则字符串加入MentionedUsers的集合中。如果匹配到的子串在原字符串的开头，就不用判断了直接加入集合。
2. 还要注意MentionedUsers不区分大小写，因此最直接的方法就是把符合要求的字符串用String.toLowerCase全部转为小写字母，再放入集合中。由于HashSet内部是可以消除重复元素的，因此可以保证内部元素的唯一性。

对应的源代码如下：

3.4.2 Problem 2: Filtering lists of tweets

（1）public static List writtenBy(List tweets, String username)

问题：返回一个列表，列表里放的是作者为username的所有tweet。

解决思路：依次扫描所有tweet，调用Tweet类的getAuthor方法，获取每条tweet的作者，与username比较，如果相同，就加入列表。

注意：还是不区分大小写，因此把username和每条tweet的作者都转化为小写之后再进行比较。

 

（2）public static List inTimespan(List tweets, Timespan timespan)

问题：返回一个列表，列表里放着的是发布时间在给出时间段内的所有tweet。

解决思路：依次扫描所有的tweet，调用Tweet类的getTimestamp方法，获取每条tweet的发布时间，用isBefore和isAfter与给出的时间段的start和end属性比较，判断是否在该时间段内，是的话就加入列表。

注意：注意判断发布时间与start/end相等的tweet也算在该时间段内。

 

（3）public static List containing(List tweets, List words)

问题：返回一个列表，列表里放的是text属性的字符串里包含给出的单词的所有tweet。

解决思路：依次扫描所有tweet，调用Tweet类的getText方法获取每一条tweet的text属性的字符串，用String.split按空格” ”进行分割，对分割出来的每一个子串与给出的words进行比较，如果相等，就加入列表。

注意：1. 要求是包含所给“单词”的字符串，因此必须是由空格分割出来的才能算单词，不考虑标点符号。

2. 不区分大小写，先用toLowerCase转化为小写字母再比较。

3.4.3 Problem 3: Inferring a social network

（1） public static Map> guessFollowsGraph(List tweets) 

问题：如果一名author在tweet中@过其他人，那么该author就会follow这些被@的人。所以Map规则为，前项表示一个用户名，后项是一个集合，集合中的元素是提到前项的用户名的所有tweet的作者。

解决思路：扫描每条tweet，调用Extract.getMentionedUsers提取出该条tweet中所有被@到的人，用map获取每个被@的人的follower集合，将author加入到每一个被@的人的follower集合中，然后重新map。

注意：如果某条tweet中某个被@的人还没有建立映射，就建立一个这个人到空集的映射。

 

（2）public static List influencers(Map> followsGraph)

问题：按照社交网络的影响力对所有用户进行排名。影响力的大小由这个人的follower数量决定。

解决思路：1. 首先由followsGraph.size获取每个人的follower的数量；

2. 建立每个人到他的follower数量的映射followerNumbers；

3. 创建一个集合，用map.keySet获取followerNumbers的关键字的集合follow_number；

4. 每次循环找follower_number中对应follower数量最多的一个用户，加入list列表中，并将他移除follower_number集合，直到集合为空。

5. 返回list。

3.4.4 Problem 4: Get smarter

(1)public static Map> MyGuessFollowsGraph(List tweets)

问题：在3.4.3.(1)的基础上，增加规则，如果A follow B,B follow C,那么A follow C。

解决思路：1. 先调用guessFollowsGraph得到一个map，获取所有人的一级follow关系；

2. 先循环map的key集合，对每一个元素key，获取他的value集合followers；

3. 遍历followers，对map的key集合中包含的元素，获取他的value集合，将集合中的所有元素加入followers。

注意：不能直接修改follower，必须先将添加的元素放到一个辅助Set中，等第3步的遍历结束后再进行合并。

4.将key与新的followers建立映射，加入map。