Hungarian Algorithm(匈牙利算法)

本文简单介绍 Hungarian Algorithm(匈牙利算法) 及其矩阵表示下的操作流程。翻译自维基百科。

匈牙利算法(Hungarian Algorithm)是一种组合优化算法(combinatorial optimization algorithm)，用于求解指派问题(assignment problem)，算法时间复杂度为 O(n3) 。Harold Kuhn发表于1955年，由于该算法基于两位匈牙利数学家的早期研究成果，所以被称作“匈牙利算法”。 —— 维基百科

1.指派问题

假设有三位工人A, B和C，需要分配他们每人完成一件工作；对于不同的工作他们索要不同的工钱，如下表所示。问题就是要找到一套开销最小的指派方案。

.	扫地	擦窗户	清理浴室
A	100 元	300元	300元
B	300 元	100元	300元
C	300 元	300元	100元

使用匈牙利方法可以找到开销最小的方案，即A负责扫地，B负责擦窗户，C负责清理浴室，总开销为300元。

2.匈牙利算法的矩阵形式

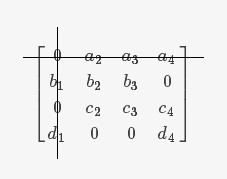
给定 n 位工人以及 n 件工作，可以用一个 n×n 的开销矩阵来表示这一指派问题：

⎡⎣⎢⎢⎢a1b1c1d1a2b2c2d2a3b3c3d3a4b4c4d4⎤⎦⎥⎥⎥

其中a，b，c和d表示工人，下标1，2，3，4表示任务； a3 表示工人a被指派完成第3项任务的开销，其余元素以此类推。

3.匈牙利算法步骤

算法核心思想：一件大的事物若除去一件小的事物，对这件事没有多大影响。——引自 [ 百度百科 ]

Step-1 对开销矩阵的各行进行操作:

找出每一行中值最小的元素，然后把该行所有元素都减去这一最小值

完成后矩阵的每一行至少会出现一个0。假如 a1,b4,c2,d3 是开销矩阵的最小值，则开销矩阵在完成本项操作后变成

⎡⎣⎢⎢⎢0b1−b4c1−c2d1−d3a2−a1b2−b40d2−d3a3−a1b3−b4c3−c20a4−a10c4−c2d4−d3⎤⎦⎥⎥⎥.

这个矩阵每行都有一个0，而且这些0分布于 不同的列，那么开销最小的指派方案就出来了，就是 a→1,b→4,c→2,d→3 。

然而问题一般并没有这么简单，执行完这一步后，开销矩阵中的0元素很可能没有分布于不同的行列(如下面的矩阵中第三列没有0)，那么继续进行下一步操作。

⎡⎣⎢⎢⎢a10c100b2c2d2a3b3c3d3a4b40d4⎤⎦⎥⎥⎥

Step-2 对开销矩阵的各列进行操作:

找出每一列中值最小的元素，然后把该列所有元素都减去这一最小值

这一步之后，如果0分布于不同的行列，则得到了最优解；如果以每个0为中心画十字(见下图)、被十字覆盖的其余0不再画十字，所有的0都画十字后仍有元素未被覆盖(图中 c3 )，则说明指派未完成，继续进行下一步。

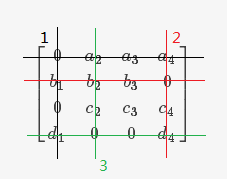
Step-3 用尽量少的横线或竖线覆盖矩阵中的所有0:

⎡⎣⎢⎢⎢0b10d1a2b2c20a3b3c30a40c4d4⎤⎦⎥⎥⎥

假设我们现在要对上面的开销矩阵进行操作。

3.1把任务尽可能多的分配给工人
(1)第一行(表示第一个人工可接受的任务)有一个0，所以把第1项任务分配给工人 a 。由于第1项任务已经分配出去，所以位于第三行第一列的0不再被考虑。

(2)第二行有一个0，所以把第4项任务分配给工人 b 。

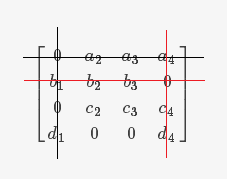
(3)第三行原本有一个0，但是由于第1项任务已经被分配出去，所以不予以考虑，不能给 c 分配任务。
(4)第四行有两个未被覆盖的0，但只能给 d 分配一项任务，另一项未被分配的任务要划掉、本轮不予以考虑。

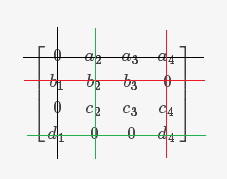
3.2 用最少的线覆盖所有0
3.2.1标记所有上一步后仍未得到任务的工人（矩阵的行）：标记第三行

3.2.2标记所有**刚被标记过的行中**0所在的列：标记第一列

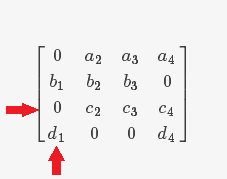
3.2.3标记所有刚被标记过的列中0所在的行：标记第一行

3.2.4对仍未得到任务的工人(矩阵的行)重复以上3步
3.2.5在所有标记过的列和未标记的行上画线

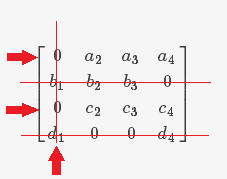
经过以上画线操作，所有的0就被以最少的线覆盖了。

Step-4

从上一步中未被覆盖的元素中找到最小值，然后把这些元素都减去最这一小值、给直线交叉点的元素加上这一最小值

被覆盖元素中的最小值实际上是完成所有任务过程中不可避免的开销。
这一步的作用是增加开销矩阵中0的个数，使得任务更易分配。

Step-5

重复Step-3和Step-4，直到所有任务都被分配

---