8.19
Path
卢姥爷太强了!!!
\((n+m-1)*\sum_{i=1}^{n+m-1}(A_i-A_{avg})^2\)
\(=……\)
\(=\sum_{i=1}^{n+m-1}[(n+m-1)*A_i^2]-\sum_{i=1}^{n+m-1}2*A_i*sum+sum^2\)
\(=\sum_{i=1}^{n+m-1}[(n+m-1)*A_i^2]-2*sum*\sum_{i=1}^{n+m-1}A_i+sum^2\)
\(=\sum_{i=1}^{n+m-1}[(n+m-1)*A_i^2]-sum^2\)
对于确定的\(sum\),只需求出式子前一部分的最小值,可以用\(DP\)来做。\(f[i][j][k]\)表示到\((i,j)\),目前所走路径的和为\(k\),所走过路径的\(\sum_{i=1}^{i+j-1}[(n+m-1)*A_i^2]\)的最小值。
调试时出错的点:
\(1.\)因为初始值为正无穷,如果用\(DP\)只表示\(\sum_{i=1}^{i+j-1}A_i^2\)的话,以为最后统计答案要乘一个\(n+m-1\),那么没更新过答案的位置会爆掉\(int\),导致最后答案为负值。
\(2.\)用\(k\)代表\(n+m-1\)时忘记了循环变量也用的\(k\)
\(3.\)第三位最大到1830(1900)就行,结果枚举边界设为了所有数的和,爆掉了
最终代码:
#include
#include
#include
using namespace std;
int n,m,a[33][33],f[33][33][2000],t;
int ans=2147483647,sum;
int main()
{
scanf("%d%d",&n,&m);
t=n+m-1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&a[i][j]);
sum=1900;
memset(f,0x3f,sizeof(f));
f[1][1][a[1][1]]=a[1][1]*a[1][1]*t;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(i==1&&j==1) continue;
for(int k=a[i][j];k<=sum;k++)
{
f[i][j][k]=min(f[i][j-1][k-a[i][j]],f[i-1][j][k-a[i][j]])+a[i][j]*a[i][j]*t;
}
}
/* for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
for(int k=a[i][j];k<=sum;k++)
{
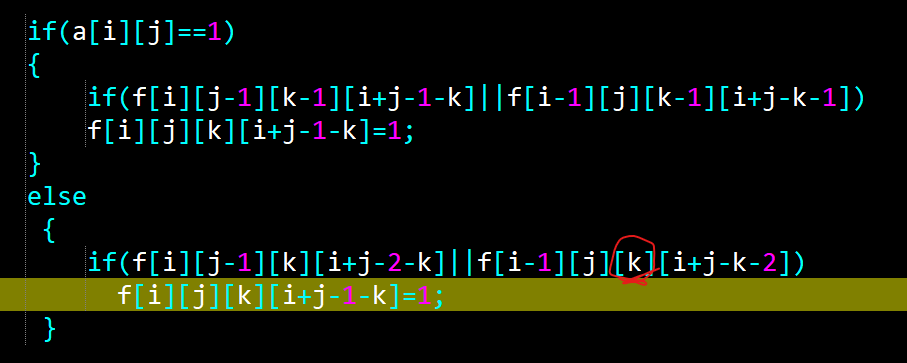
// cout< 考试时,这里写成了\(k-1\)
Rect
调到死亡。。。。
错点:
\(1.\)
不能用\(ST\)表维护一段区间的最小值
原因:
只用它向左扩展到最远位置中高度的最小值,会漏掉答案(假设红色是答案),只会计算到橙色的。
(考试时的错点)
\(2.\)
关于单调队列,等于的时候是要退出的。假如当前点进队之前对中没有元素,那么它左边(或右边)没有比它矮的,最矮的就记为它自己。
\(3.\)
关于统计答案,不能只统计两边最小。这样漏掉了以该点向上的高度为最小值(答案的高)的答案。
所以要: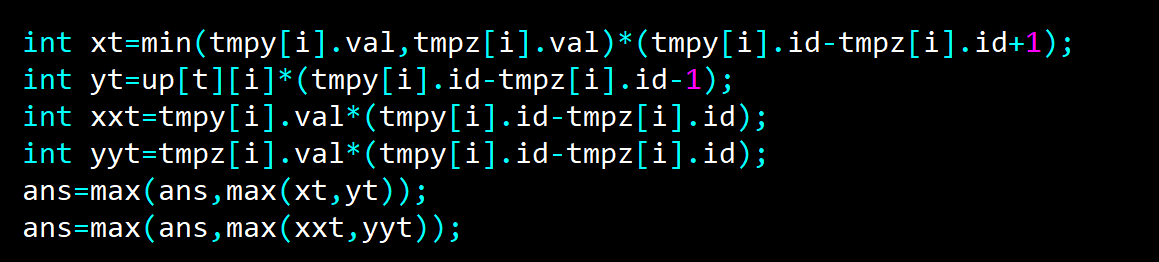
\(4.\)
假如第\(i\)行第\(r\)个点向前最长的等差数列到位置\(l\),这算一个区间,那么下一个区间的\(r\)不能从\(l-1\)开始,而要从\(l\)开始。
\(5.\)
奇怪的算法还是不要写了,悬线法好哇!
但还不知道为啥错。
(\(work\)和\(work1\)类似)
\(6.\)
选出一段等差数列的区间后,再从中选公差为等差数列的区间时,必须在先选出的等差数列的区间内。
因为循环结束后会\(j--\),所以\(j\)要开大一个。但如果不特判\(r==x\)时,可能会陷入一直是\(x\)到\(x\)区间的死循环。
终极版代码:
#include
#include
#include
using namespace std;
const int N = 1005;
int n,m,a[N][N],up[N][N],gc[N][N];
int l1,r1,l2,r2,l,r,ans,lef[N][N],lefg[N][N];
struct node{
int val,id;
}q1[N],q2[N],tmpz[N],tmpy[N];
void work(int t,int x,int y)
{
l1=l2=1; r1=r2=0;
for(int i=x;i<=y;i++)
{
while(r1&&q1[r1].val>=up[t][i]) --r1;
if(r1<=0) tmpz[i].val=up[t][i],tmpz[i].id=x;
else tmpz[i].val=q1[r1].val,tmpz[i].id=q1[r1].id;
q1[++r1].val=up[t][i]; q1[r1].id=i;
}
for(int i=y;i>=x;i--)
{
while(r2&&q2[r2].val>=up[t][i]) --r2;
if(r2<=0) tmpy[i].val=up[t][i],tmpy[i].id=y;
else tmpy[i].val=q2[r2].val,tmpy[i].id=q2[r2].id;
q2[++r2].val=up[t][i]; q2[r2].id=i;
}
for(int i=x;i<=y;i++)
{
int xt=min(tmpy[i].val,tmpz[i].val)*(tmpy[i].id-tmpz[i].id+1);
int yt=up[t][i]*(tmpy[i].id-tmpz[i].id-1);
int xxt=tmpy[i].val*(tmpy[i].id-tmpz[i].id);
int yyt=tmpz[i].val*(tmpy[i].id-tmpz[i].id);
ans=max(ans,max(xt,yt));
ans=max(ans,max(xxt,yyt));
}
return ;
}
/*void work1(int t,int x,int y)
{
l=x; r=x+1;
while(l<=y&&r<=y)
{
int ch=gc[t][r]-gc[t][l];
while(gc[t][r]-gc[t][r-1]==ch&&r<=y+1) ++r;
--r;
work(t,l,r);
l=r; r=l+1;
}
}*/
void work1(int t,int x,int y)
{
int r;
for(int j=y;j>=x;j--)
{
r=j+1-lefg[t][j];
work(t,max(r,x),max(x,j));
if(r!=x) j=r+1; //
else j=r; //
}
}
int main()
{
// freopen("rect.in","r",stdin);
// freopen("rect.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
gc[i][j]=a[i-1][j]-a[i][j];
if(i>1) up[i][j]=2;
else up[i][j]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(gc[i][j]==gc[i-1][j])
up[i][j]=up[i-1][j]+1;
}
for(int i=1;i<=n;i++)
{
lef[i][1]=1; lef[i][2]=2;
for(int j=3;j<=m;j++)
{
if(a[i][j]-a[i][j-1]==a[i][j-1]-a[i][j-2])
lef[i][j]=lef[i][j-1]+1;
else lef[i][j]=2;
}
}
for(int i=1;i<=n;i++)
{
lefg[i][1]=1; lefg[i][2]=2;
for(int j=3;j<=m;j++)
{
if(gc[i][j]-gc[i][j-1]==gc[i][j-1]-gc[i][j-2])
lefg[i][j]=lefg[i][j-1]+1;
else lefg[i][j]=2;
}
}
/* for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cout<=1;j--)
{
r=j+1-lef[i][j];
work1(i,r,j);
if(r!=1) j=r+1; //
else j=r; //
}
}
/* for(int i=1;i<=n;i++)
{
l=1;r=2;
while(l<=m&&r<=m)
{
int ch=a[i][r]-a[i][l];
while(a[i][r]-a[i][r-1]==ch&&r<=m+1) ++r;
--r;
work1(i,l,r);
l=r; r=l+1;
}
}*/
printf("%d\n",ans);
return 0;
}