leetcode经典排列问题

推荐题目

LeetCode 上有几道题都和排列组合有关，非常经典，值得放在一起总结一下。这几道题分别是：

• Permutations。给定一组各不相同的数字，求这些数字的所有排列。
• Permutations II。给定一组数字，这些数字中可能有重复的，求这些数字的所有不重复的排列。
• Next Permutation。给定一组数字的全排列中的一个排列，求这个排列的下一个排列。
  Permutation Sequence。给定一组数字和一个数字 K，求这组数字的全排列中，按照字典序顺序排序的第 K 个排列。
• 1079. 活字印刷 给定一组数字，这些数字中可能有重复的，求构造这些数字所有不重复排列过程中搜索树产生的节点。

Permutations

对于一个集合来说，它的全排列是指集合内元素的所有可能的排列。以输入[1,2,3]为例，它的全排列是[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]这六种情况。求一个集合的全排列有很多种方法，本文中将介绍一下最为常见的两种方法，字典序法和递归法。

字典序法——nextPermutation

时间复杂度：$O(n\ast n!)$，其中 $n$ 为序列的长度。

效率低于递归

要找到所有排列，需要先排序

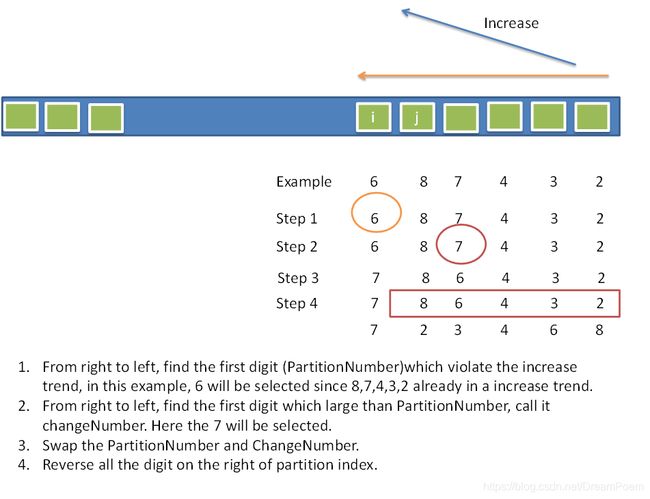
字典序法，就是将元素按照字典的顺序进行排列，而对于数字来说，就是将较小的数字排在较大的数字的前面。上面列出的[1,2,3]的全排列就是按照字典序的顺序排列的。由输入排列产生下一排列时，字典序法要求它与当前排列有尽可能长的公共前缀，因此针对输入的1,2,3，使用字典序法生成全排列，就是依次生成1,3,2，2,1,3，2,3,1，3,1,2，3,2,1。那么如何根据当前排列来生成下一排列呢？

已知当前排列，求下一排列的算法过程：

1. 对于给定排列nums,从右向左，找出第一个违反从右到左是递增顺序的数字，记为i。以[6,8,7,4,3,2]为例，从右向左一直是增加的，直到6的出现打破了这一规律，因此i = 6。
2. 从右向左，找出第一个比刚刚找到的数字大的数字，记为j。对于[6,8,7,4,3,2]，从右到左依次是2,3,4,7，因此这个数字是7，j=7。
3. 交换这两个数字。即将[6,8,7,4,3,2]中的6和7进行交换，变为[7,8,6,4,3,2]。
4. 将j右边的所有数字进行逆序，即将7右边的[8,6,4,3,2]逆序，[7,8,6,4,3,2]变为[7,2,3,4,6,8]。算法结束。

版本一

此版本返回Boolean，当输入数组为完全逆序数组，即字典序最大时返回false。

	public boolean nextPermutation(int[] nums, int lo, int hi) {
        if (lo == hi) return false;
        int n = hi - lo;

        int violationIndex = hi - 1;
        while (violationIndex > 0) {
            // 从右向左找到第一个，违反递增顺序的数: nums[violationIndex - 1]
            if (nums[violationIndex] > nums[violationIndex - 1]) break;
            violationIndex--;
        }

        if (violationIndex > 0) {
            // 从右向左第一个违反递增顺序的数nums[violationIndex]
            violationIndex--;
            int changeIndex = hi - 1;
            // 从右向左找到第一个大于nums[violationIndex]的数nums[changeIndex]
            while (nums[changeIndex] <= nums[violationIndex]) changeIndex--;
            
            // 交换nums[violationIndex] 与 nums[changeIndex]
            nums[violationIndex] = nums[violationIndex] ^ nums[changeIndex] ^
                    (nums[changeIndex] = nums[violationIndex]);
            
            // 将nums[violationIndex..hi)的数进行逆序
            for (int i = violationIndex + 1, j = hi - 1; i < j; i++, j--) {
                nums[i] = nums[i] ^ nums[j] ^ (nums[j] = nums[i]);
            }
            return true;
        }
        // return false表明nums已经完全是一个逆序数
        return false;
    }

注意：

1. nextPermutation要想找到数组元素的全排列，要求数组初始化必须是有序的。
2. nextPermutation可以处理含有重复元素数组的全排列

版本二

此版本返回void，当输入数组为字典序最大的排列时，下一个排列为字典序最小的排列。

	public void nextPermutation(int[] nums) {
        int n = nums.length;
        if (n == 0) return;

        int violationIndex = n - 1;
        while (violationIndex > 0) {
            if (nums[violationIndex] > nums[violationIndex - 1]) break;
            violationIndex--;
        }

        if (violationIndex > 0) {
            violationIndex--;
            int changeIndex = n - 1;
            while (nums[changeIndex] <= nums[violationIndex]) changeIndex--;
            nums[violationIndex] = nums[violationIndex] ^ nums[changeIndex] ^ (nums[changeIndex] =
                    nums[violationIndex]);
            violationIndex++;   
        }
        
        for (int i = violationIndex, j = n - 1; i < j; i++, j--) {
            nums[i] = nums[j] ^ nums[i] ^ (nums[j] = nums[i]);
        }
        return;
    }

不含重复元素的全排列

对于一个集合来说，它的全排列是指集合内元素的所有可能的排列。以输入[1,2,3]为例，它的全排列是[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]这六种情况。求一个集合的全排列有很多种方法，本文中将介绍一下最为常见的两种方法，字典序法和递归法。

从集合中依次选出每一个元素，作为排列的第一个元素，然后对剩余的元素进行全排列，如此递归处理，从而得到所有元素的全排列。以对[1,2,3]进行全排列为例，我们可以这么做：

	private List<List<Integer>> permutations = new ArrayList<>();

    private void swap(int[] nums, int i, int j) {
        nums[i] = nums[i] ^ nums[j] ^ (nums[j] = nums[i]);
    }

    private void permutation(int[] nums, int lo, int hi) {
        if (lo + 1 == hi) {
            permutations.add(Arrays.stream(nums).boxed().collect(Collectors.toList()));
            return;
        }

        for (int i = lo; i < hi; i++) {
            swap(nums, lo, i);  // 取nums[i]作为"首个"排列数
            permutation(nums, lo + 1, hi);
            swap(nums, lo, i);  // 回溯
        }

    }

注意：

private void permutation(int[] nums, int lo, int hi)不能处理含有重复元素的数组的全排列。

时间复杂度：$O(n\ast n!)$，其中 $n$ 为序列的长度。

含有重复元素的全排列

假设含有重复元素duplication，在递归的过程中只要限制只有第一个duplication位于排头即可。即对于非第一个duplication不做处理，判别方法如下：

for (int j = lo; j < i; j++) if(nums[i] == nums[j]) continue lable;

nums[lo..i)中至少存在一个nums[j]==nums[i]时，便不需交换nums[j],nums[lo]。因为nums[j]已经与nums[lo]交换过一次。

class Solution {
    private List<List<Integer>> permutations = new ArrayList<>();

    private void swap(int[] nums, int i, int j) {
        nums[i] = nums[i] ^ nums[j] ^ (nums[j] = nums[i]);
    }

    /**
     * nums需是有序数组，为了使重复字符安排在相邻位置！
     */
    private void permutation(int[] nums, int lo, int hi) {

        if (lo + 1 == hi) {
            permutations.add(Arrays.stream(nums).boxed().collect(Collectors.toList()));
            return;
        }

        lable:
        for (int i = lo; i < hi; i++) {
            // 如果nums[lo..i)中存在nums[j]==nums[i]
            // 说明nums[j]已经成为过排头了，便不需再操作nums[i]了
            for (int j = lo; j < i; j++) if(nums[i] == nums[j]) continue lable;
            if (nums[lo] != nums[i]) swap(nums, lo, i);  // 取nums[i]作为"首个"排列数
            permutation(nums, lo + 1, hi);
            if (nums[lo] != nums[i]) swap(nums, lo, i);  // 回溯
        }

    }
    
    public List<List<Integer>> permuteUnique(int[] nums) {
        if (nums.length == 0) return new ArrayList<>();
        permutation(nums, 0, nums.length);
        return permutations;
    }
}

Kth Permutation

见leetcode解题报告——60. 第k个排列