CUDA(六). 从并行排序方法理解并行化思维——冒泡、归并、双调排序的GPU实现
在第五讲中我们学习了GPU三个重要的基础并行算法: Reduce, Scan 和 Histogram,分析了 其作用与串并行实现方法。 在第六讲中,本文以冒泡排序 Bubble Sort、归并排序 Merge Sort 和排序网络中的双调排序 Bitonic Sort 为例, 讲解如何从数据结构课上学的串行并行排序方法转换到并行排序,并附GPU实现代码。
在并行方法中,我们将考虑到并行方法需要注意的特点进行设计,希望大家在读完本文后对GPU上并行算法的设计有一些粗浅的认识。需注意的特点如下:
1. 充分发挥硬件能力(尽量不要有空闲且一直处于等待状态的SM)
2. 限制branch divergence(见CUDA系列学习(二))
3. 尽量保证内存集中访问(即防止不命中)
( 而我们在数据结构课上学习的sort算法往往不注意这几点。)
CUDA系列学习目录:
CUDA系列学习(一)An Introduction to GPU and CUDA
CUDA系列学习(二)CUDA memory & variables - different memory and variable types
CUDA系列学习(三)GPU设计与结构QA & coding练习
CUDA系列学习(四)Parallel Task类型 与 Memory Allocation
CUDA系列学习(五)GPU基础算法: Reduce, Scan, Histogram
I. Bubble Sort
冒泡排序,相信大家再熟悉不过了。经典冒泡排序通过n轮有序冒泡(n为待排序的数组长度)得到有序序列, 其空间复杂度O(1), 时间复杂度O(n^2)。
那么如何将冒泡排序算法改成并行算法呢? 这里就需要解除一些依赖关系, 比如是否能解除n轮冒泡间的串行依赖 & 是否能解除每一轮冒泡内部的串行依赖, 使得同样的n^2次冒泡操作可以通过并行, 降低step complexity。
1996年, J Kornerup针对这些问题提出了odd-even sort算法,并在论文中证明了其排序正确性。
I.1 从Bubble Sort到Odd-even Sort
先来看一下odd-even sort的排序方法:

图1.1
上图为odd-even sort的基本方法。
奇数步中, array中奇数项array[i]与右边的item(array[i + 1])比较;
偶数步中, array中奇数项array[i]与左边的item(array[i - 1]) 比较;
这样,同一个step中的各个相邻比较就可以并行化了。
PS: 对于array中有偶数个元素的数组也是一样:
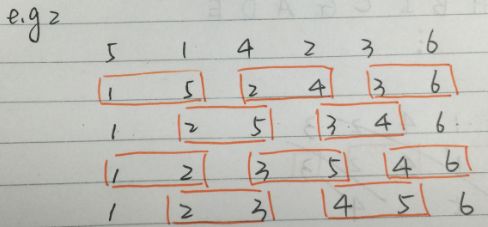
图1.2
I.2 Odd-even Sort复杂度
在odd-even sort的算法下, 原本O(n^2)的总比较次数不变,但是由于并行,时间复杂度降到O(n), 即
step complexity = O(n)
work complexity = O(n^2)
code详见 < Bubble sort and its variants >
II. Merge Sort
看过odd-even sort后,我们来看如何将归并排序并行化。数据结构课上我们都学过经典归并排序: 基于divide & conquer 思想, 每次将一个array分拆成两部分, 分别排序后合并两个有序序列。 可以通过 T(n)=2T(n/2)+n 得到, 其complexity = O(nlogn)。 和I.1节类似, 我们看看merge sort中的哪些步是可以并行的。
这里可以将基于merge sort的大规模数据排序分为三部分。 经过divide步之后, 数据分布如图所示:

图2.1
最下端的为 大量-短序列 的合并;
中间一块为中等数量-中等长度序列 的合并;
最上端的为少量-长序列 的合并;
我们分这三部分进行并行化。 之后大家会明白为啥要这么分~
II.1 Step 1: Huge number of small tasks
这一部分,每一部分序列合并的代价很小, 而有众多这样的任务。 所以我们采取给每个merge一个thread去执行, thread 内部就用串行merge的方法。
II.2 Step 2: Mid number of mid task
在这一阶段, 有中等数量的task, 每个task的工作量也有一定增长。 所以我们采取给每个merge一个SM去执行, 每个block上运行的多个thread并行merge的方法。 和step1中的主要区别就是block内部merge从串行改成了并行。 那么怎样去做呢?
如下图所示,假如现在有两个长为4个元素的array, 想对其进行排序, 将merge排序结果index 0 - 7 写入数据下方方块。
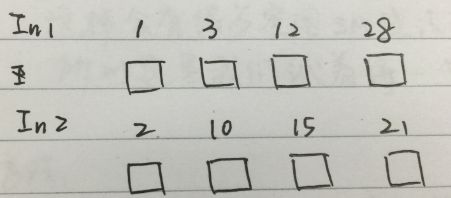
图2.2
做法:
对于array中的每个数字, 看两个位置:
1. 自己所在序列的位置: 看它前面有几个元素
2. 另一个序列的位置: 另一个序列中有多少个元素比它小(采用二分搜索)
这样做来, 第一步O(1)可得到, 第二步二分查找O(logn)可得到; 整个merge过程用shared memory存结果。
II.3 Step 3: Small number of huge task
第三个环节中,也就是merge的顶端(最后一部分),每个merge任务的元素很多, 但是merge任务数很少。 这种情况下, 如果采用Step2的方法, 最坏的情况就是只有一个很大的task在跑, 此时只有1个SM在忙, 其他空闲SM却没法利用, 所以这里我们尝试将一个任务分给多个SM执行。
方法: 如图2.3所示, 将每个序列以256个元素为单位分段, 得到两个待merge序列In1和In2。然后,对这些端节点排序,如EABFCGDH。 如step2中的方法, 我们计算每个段节点在另一个短序列(长256)中的位置, 然后只对中间那些不确定的部分进行merge排序, 每个merge分配一个SM。
如E~A的部分,
1. 计算出E在In1中的位置posE1, A在In2中的位置posA2
2. merge In1中 posE1~A 和 In2中 E~posA2的元素

图2.3
II.4 Merge sort in GPU
以上面step 1的merge sort为例, 其gpu代码中kernel函数如下:
其中temp为排好序的序列, 每次排序两个大小为sortedsize的block,为temp赋值2 * sortedsize个元素。
所以实际上,sortedsize就是一个sorted block的大小。
__global__ void mergeBlocks(int *a, int *temp, int sortedsize)
{
int id = blockIdx.x;
int index1 = id * 2 * sortedsize;
int endIndex1 = index1 + sortedsize;
int index2 = endIndex1;
int endIndex2 = index2 + sortedsize;
int targetIndex = id * 2 * sortedsize;
int done = 0;
while (!done)
{
if ((index1 == endIndex1) && (index2 < endIndex2))
temp[targetIndex++] = a[index2++];
else if ((index2 == endIndex2) && (index1 < endIndex1))
temp[targetIndex++] = a[index1++];
else if (a[index1] < a[index2])
temp[targetIndex++] = a[index1++];
else
temp[targetIndex++] = a[index2++];
if ((index1 == endIndex1) && (index2 == endIndex2))
done = 1;
}
}
主函数中,定义block大小并调用kernel function:
int blocks = BLOCKS/2;
int sortedsize = THREADS;
while (blocks > 0)
{
mergeBlocks<<1>>>(dev_a, dev_temp, sortedsize);
cudaMemcpy(dev_a, dev_temp, N*sizeof(int), cudaMemcpyDeviceToDevice);
blocks /= 2;
sortedsize *= 2;
}
cudaMemcpy(a, dev_a, N*sizeof(int), cudaMemcpyDeviceToHost);
III. Bitonic Sort
III.1 Bitonic Sequence 双调序列
不同于以上两种排序方法, 现在我们要接触的 双调排序 是排序网络方法中的一种。 想起当年在浙大面试某导师的实验室时就是让实现的双调排序, 并不断优化, 不过当时土得一坨, 就没听说过这个算法。。。 最后写出个多线程就结束了, 后来也没再整理。 现在我们来看看bitonic sort是个什么鬼。
双调排序是排序网络中最快的方法之一。所谓的排序网络是data-independent的排序, 即网络比较顺序与数据无关的排序方法, 所以特别适合硬件做并行化。
在了解双调排序算法之前,我们先来看看什么是双调序列。 双调序列是一个先单调递增后单调递减 或者 先单调递减后单调递增的序列。
III.2 双调排序算法
假如我们现在拿到了双调序列, 怎样对它按照从小到大进行排序呢?形象一点来看, 我们将一个双调序列切成两半, 每一段的单调性统一, 然后如下图图3.1所示, 将两段叠放起来, 进行两两比较, 这样一定能够在左右两段分别得到一个双调序列(想想为什么得到的是两个双调序列), 且左边的双调序列中元素全部小于右侧得到的双调序列的所有元素。 迭代这个过程, 每次都能将序列二分成两个子双调序列, 直到这个子双调序列的长度为2, 也就变成了一个单调子序列, 这个过程排序后原先的长双调序列就变为有序了 。 整个过程如下图图3.2所示。

图3.1

图3.2
III.3 任意序列生成双调序列
好,III.2中讲了怎样对双调序列进行排序, 那问题来了,怎样从任意序列生成双调序列呢? 这里可以看看本文最后的参考文献3, 写得很详细。 这个过程叫Bitonic merge, 实际上也是divide and conquer的思路。 和III.2中的思路正相反, 我们可以将两个相邻的,单调性相反的单调序列看作一个双调序列, 每次将这两个相邻的,单调性相反的单调序列merge生成一个新的双调序列, 然后排序(同III.2)。 这样只要每次两个相邻长度为n的序列的单调性相反, 就可以通过连接得到一个长度为2n的双调序列。 n开始为1, 每次翻倍,直到等于数组长度, 就只需要一遍单方向(单调性)排序了。
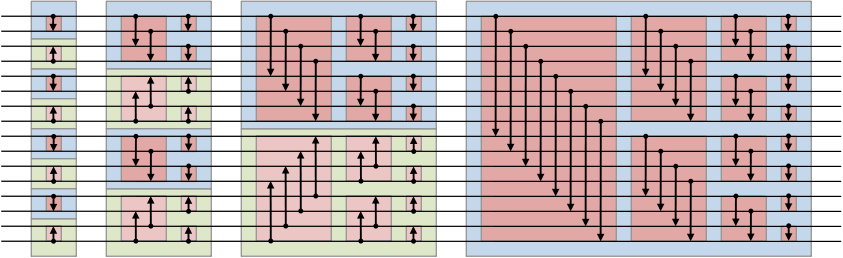
图3.3
以16个元素的array为例,
1. 相邻两个元素合并形成8个单调性相反的单调序列,
2. 两两序列合并,形成4个双调序列,分别按相反单调性排序
3. 4个长度为4的相反单调性单调序列,相邻两个合并,生成两个长度为8的双调序列,分别排序
4. 2个长度为8的相反单调性单调序列,相邻两个合并,生成1个长度为16的双调序列,排序
总算讲完了,那么肿么实现呢? 我们看这个过程需要控制哪些地方? 如上图所示, 我们可以将len=16的array的双调排序分成4部分,每一部分结束都会形成若干长度为 i 的单调序列。 在每一部分中,用 j 表示比较的间隔,如下图所示每一时刻的i和j。
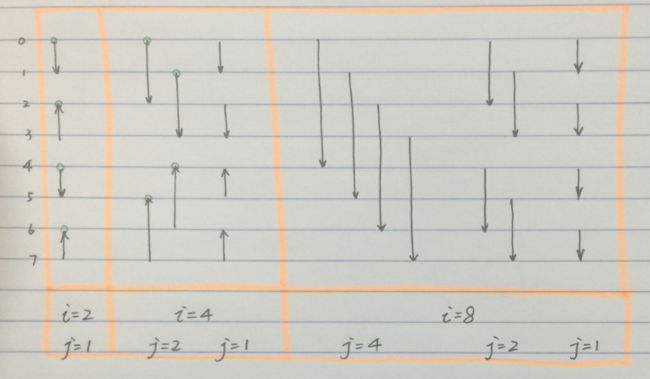
图3.4
III.4 双调排序的并行实现
本着“talk is cheap, show me the code”的优良作风, 拿粗来双调排序的GPU实现代码share如下:
/*
* Author: Rachel
*
*
* File: bitonic_sort.cu
* Create Date: 2015-08-05 17:10:44
*
*/
#includeint main(int argc, char* argv[])
{
GPUTimer timer;
int* arr= (int*) malloc(Num*sizeof(int));
//init array value
time_t t;
srand((unsigned)time(&t));
for(int i=0;i1000;
}
//init device variable
int* ptr;
cudaMalloc((void**)&ptr,Num*sizeof(int));
cudaMemcpy(ptr,arr,Num*sizeof(int),cudaMemcpyHostToDevice);
for(int i=0;iprintf("%d\t",arr[i]);
}
printf("\n");
dim3 blocks(NBlocks,1);
dim3 threads(NThreads,1);
timer.start();
bitonic_sort<<sizeof(int)>>>(ptr);
//bitonic_sort<<<1,Num,Num*sizeof(int)>>>(ptr);
timer.stop();
cudaMemcpy(arr,ptr,Num*sizeof(int),cudaMemcpyDeviceToHost);
for(int i=0;iprintf("%d\t",arr[i]);
}
printf("\n");
cudaFree(ptr);
return 0;
}
code中,
tid^j用于单方向判断, 防止同一元素比较两次;
tid & i == 0 用于判断这个部分应该是单增还是单减, 因为方向在每个长为i的单调序列中是一致的, 所以选用i判断单调方向。
参考文献:
1. Bubble sort and its variants
2. nvidia的mergesort实现
3. 我用过的浅显易懂的Bitonic sort文档
欢迎大家交流