C++编写算法（七）——平衡查找树

一、二叉树的问题

二叉树虽然能够实现高效的搜索功能，但树的建立条件比较苛刻。当树根结点如果选取不好(选取的树根结点是所有键值中较小的值或较大的值)时，二叉树的根结点的左子树可能比较丰满，右子树比较贫瘠(树根结点取较小值时)；或者左子树比较贫瘠，右子树比较丰满(树根结点取较大值时)。这就造成了搜索不同的子结点的时间不一样。如果考虑极端情况，用户输入的键值对是有序的，则树就会退化为链表，那么其搜索复杂度又会回归链表的复杂度。为了避免这种情况发生，可以要求用户输入一个比较适中的根结点，但这样显得不智能。因此，平衡查找树营运而生。

二、平衡查找树

平衡查找树是指树底的每一个空键到根结点所经过的结点数是一样的。换句话说，就是同一层的结点到根结点的路径是一样的。
如何实现：考虑到二叉树是不可能实现平衡的效果的，那么每一个树节点就需要进行进化。每一个树节点能否存储两个键值key1,key2，而它存在3个指针left, middle, right，left左指针指向小于key1的键，middle中指针指向大于key1又小于key2的键，right右指针指向大于key2的键。因此，形成了一个2-3树结点，2-3树结点的组合，便形成了一个2-3树，该树是可以实现平衡性的。
以下是《算法》对2-3查找树的定义

定义：一棵2-3查找树或为一棵空数，由以下结点组成
2-结点：含有一个键（及其对应的值）和两条链接，左链接指向的2-3树中的键都小于该节点，右链接指向的2-3树中的键都大于该结点。
3-结点：含有两个键（及其对应的值）和三条链接，左链接指向的2-3树中的键都小于该结点，中链接指向的2-3树中的键都位于该结点的两个键之间，右链接指向的2-3树中的键都大于该结点。

[图片上传失败...(image-8e180e-1556204509327)]

1、查找

2-3树的查找和二叉树的查找思路是一样的，只不过2-3树的3-结点多了一个中间指针。

2、插入

增加树节点中的Key值使得2-3树的插入变得比较复杂了。需要按照出现的每一种情况进行分析。
2-3树的插入主要分为以下几种情况：
a、向2-结点插入一个新键
如果确认需要插入的结点为新结点(没有在树中查找到相应的键值)，为了保持2-3树的平衡性，直接将2-结点进化为3-结点即可。
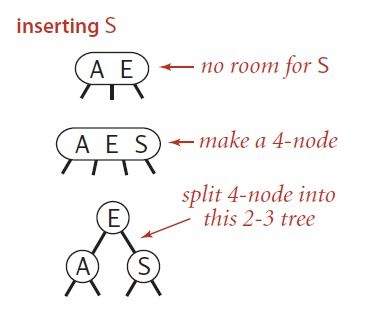
b、向只含有3-结点的一颗树中插入一个新键
向3-结点中插入一个新键比上述的2-结点插入新键要麻烦得多。首先分析只含有3-结点的树中插入新键。只含有3-结点的树中插入新键需要将这个3-结点变为一个临时的4-结点(存储3个键值，有4个指针)，然后将位于中间的键值分离出来，成为它的左右键值的父结点，然后将其左子结点赋值为4-结点的左边结点，右子结点赋值为4-结点的右边结点。

示例b(引用“寒江独钓”博客图).png

c、向一个父结点为2-结点的3-结点插入一个新键
情况b适用于树根的生长。在非树根部分的3-结点插入新键还需要考虑其父结点的属性。当父节点为2-结点时，插入的新键首先与3-结点结合成一个临时的4-结点，然后，按照情况b的方式分解，然后其中间结点与父2-结点结合形成一个新的3-结点。

示例c(引用“寒江独钓”博客图).png

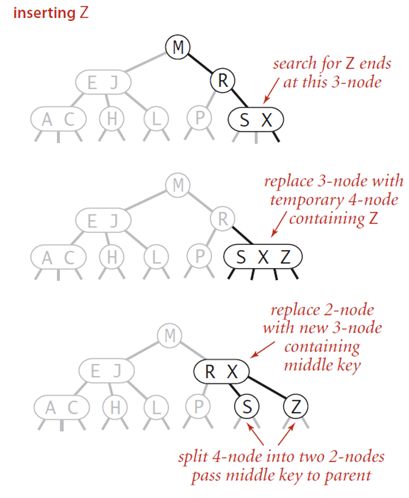
d、向一个父结点为3-结点的3-结点插入一个新键
当3-结点的父结点也为3-结点时，情况更加复杂。首先，插入目标3-结点需要变成一个临时4-结点，按照情况b进行分解。该临时4-结点中的中间键值与父结点又组成一个临时4-结点，然后再进行情况b的分解。这种情况子树中不断产生一个新的树根，不断向上生长，直至碰见一个2-结点为止。

示例d(引用“寒江独钓”博客图).png

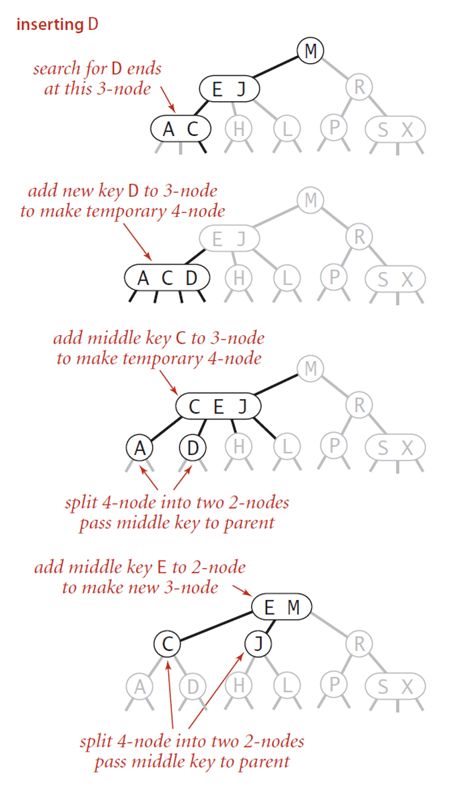
e、向一个叶结点全部为3-结点的树中插入一个新键
这种极端情况是情况d中，树插入处因碰到3-结点而不断向上生长的情况。这种情况一直延续至根节点，当根节点为一个临时4-结点时，将中间键值作为新的树根，按照情况情况b的方式进行分解，得到一个比原树层数多1层的新树。

树高为N的2-3树中，查找和插入操作访问的结点必然不超过lgN个

2-3树有着非常高效的查找性能。但是要实现这样的2-3树十分地复杂，代码既需要维护2-结点的属性，又需要维护3-结点的属性。并且，代码额外产生的花销可能会影响2-3树的性能。
幸运的是，大神们研究出了一种可以代替或者等效2-3树的方法——红黑平衡树。

三、红黑平衡树

1、原理

根据2-3树的思想，可以用一种二叉树的表达替代2-3树。替代2-3树的关键点在于3-结点的替换。红黑平衡树采用颜色链接的方式代替3-结点。若叶结点之间的链接为红色的，则这两个节点组成一个3-结点，其余链接均为黑色链接。
《算法》中对红黑树实现2-3树提出一种等价的定义

·红链接均为左链接
·没有任何一个节点同时和两条红链接相连
·树是黑色完美平衡的

2、实现

红黑树的实现其实可以在原来树的基础上实现。主要是在叶结点处添加一个颜色变量，代表指向该结点的指针颜色。
红黑树的叶结点结构如下:

template
struct TreeNode
{
    T key;
    int value;
    TreeNode* leftChild = NULL;
    TreeNode* rightChild = NULL;
    bool color = false;              // True is red, false is black
};

这里将颜色变量设置为布尔类型，也可以将它设置为枚举类型。
构建叶结点后，我们需要根据上述的等价定义规则，实现一个红黑平衡树。对于“红链接都是左链接”以及“没有任何一个节点同时和两条红链接相连”这两个要求，需要展开详细的分析。
在插入时红链接不仅会出现在左链接处，也会出现在右链接处。因此，我们需要对红链接进行操作，使其变为恒左链接，这个操作为旋转。
旋转分为左旋转和右旋转。
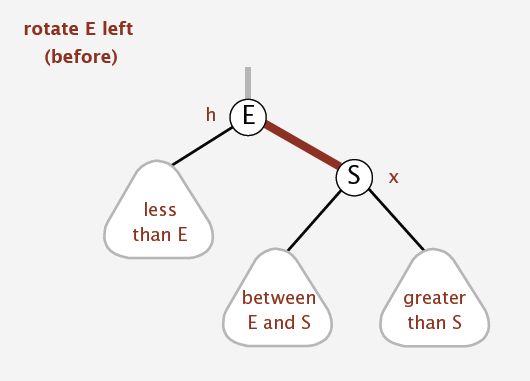
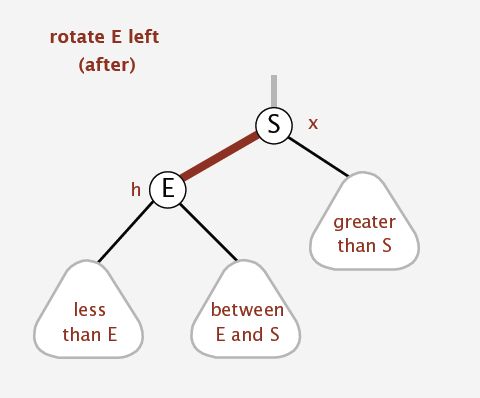
-左旋转的情况为：当前的红链接为右链接，如图

左旋转情况(引用“寒江独钓”博客图).png

该图中的E结点的右链接为红链接，不符合定义，需要进行左旋转。左旋转后，父结点变为S结点，S结点的左链接为红链接，链接结点E。
左旋转后的结果为：

左旋转后的结果(引用“寒江独钓”博客图).png

所以，左旋转操作为：

template
TreeNode* Tree::leftRotation(TreeNode* t)
{
    TreeNode* x = t->rightChild;
    t->rightChild = x->leftChild;
    x->leftChild = t;
    x->color = t->color;
    t->color = true;
    return x;
}

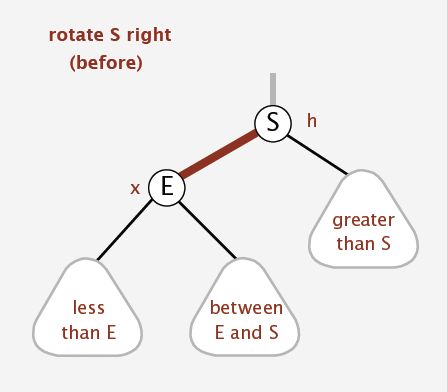
-右旋转的情况需要根据再上层的结点进行分析，先指出右旋转是必要的。

右旋转情况(引用“寒江独钓”博客图).png

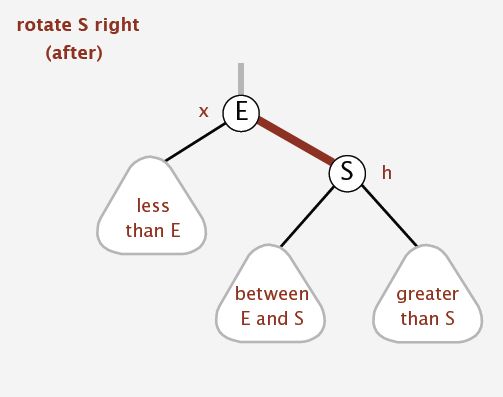
此时需要我们进行右旋转，则将E结点设置为父结点，其右指针变为红色，指向S结点。

右旋转结果(引用“寒江独钓”博客图).png

则右旋转操作为：

template
TreeNode* Tree::rightRotation(TreeNode* t)
{
    TreeNode* x = t->leftChild;
    t->leftChild = x->rightChild;
    x->rightChild = t;
    x->color = t->color;
    t->color = true;
    return x;
}

小记：这里左旋转(右旋转也相似)需要注意语句

    t->rightChild = x->leftChild;
    x->leftChild = t;

的顺序。这里我们设t为原始根节点，x为子结点。需要做的操作是先将t的右子结点指向x的左子结点，即先对其他不操作的结点进行保存和移动，再将x节点的左子结点置为t，完成旋转。如果这两个语句顺序颠倒，将会出现t节点与x节点的右子和左子相互连接，形成一个死循环。
分析完旋转的情况后，在旋转的基础上，分析插入新的叶结点的情况。与2-3树的插入情况类似，我们也要分析向红黑树中插入新的结点有哪些情况，通过代码解决不同情况带来的问题。
(插入时均把结点的连接置为红链接)
(1)、向单个2-结点插入新键(即向一个黑连接的叶结点插入新键)
这种情况因树的平衡性，需要考虑旋转。插入时，若键值大于当前结点，则连接到当前结点的右子结点，链接颜色置为红色，此时与左旋转的情况相同，因此进行左旋转操作。若键值小于当前结点，该情况比较简单，连接到当前结点的左子结点，连接颜色置为红色。
(2)、向单个3-结点插入新键
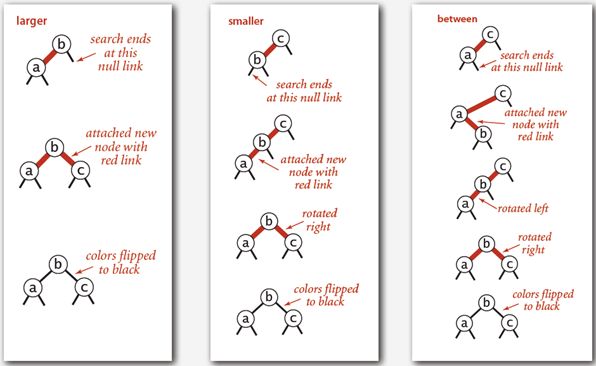
向单个3-结点插入新键有3种情况，即插入结点落在左指针、中间指针以及右指针上。 情况如下：

三种情况(引用“寒江独钓”博客图).png

-落在右指针上时，情况比较简单，树已经实现平衡，但因左链接和右链接不可同时为红链接，因此。将b的左子和右子颜色均置为黑色，实现插入。
-落在左指针上时，情况如中间的图所示，此时树链接出现了连续红色左链接。因此，将b结点与c结点进行右旋转，得到左图情况，按左图方式进行操作。
-落在中间指针上时，情况如右图所示，此时树出现一个红色左链接接上一个红色右链接的情况。因此，先对a结点与b结点进行左旋转，得到中间的图的情况，再按中间的图的情况进行右旋转，得到左图的情况，最后按左图方式进行操作。
插入的情况分析完毕后，还需要分析树链接的颜色，按照(1)(2)两种情况进行插入后，红链接需要向上传递，以此来保证树每层处理的合理性，保证树的黑色平衡。同时需要指出，根节点的链接一定是黑色的。
红黑树的构建：

#ifndef MYTREE_H_
#define MYTREE_H_
#include 
#include 
#include 

template
struct TreeNode
{
    T key;
    int value;
    TreeNode* leftChild = NULL;
    TreeNode* rightChild = NULL;
    bool color = false;              // True is red, false is black
    //TreeNode(T k, int v, bool c) { key = k, value = v, leftChild = NULL, rightChild = NULL, color = c; }
    //TreeNode() {}
};

template
class Tree
{
private:
    TreeNode* leftRotation(TreeNode* t);
    TreeNode* rightRotation(TreeNode* t);
    void flipColor(TreeNode* t);
    bool isRed(TreeNode* t);
    TreeNode* insert_ac(TreeNode* t, TreeNode* t2);

protected:
    TreeNode* root;

public:
    Tree();
    ~Tree();
    bool isempty();
    void insert(TreeNode* t);
    void layerOrder();
    void Show(TreeNode* t) const;
};

#endif // !MYTREE_H_

#pragma region PRIVATE METHODS
// private color method 
template
bool Tree::isRed(TreeNode* t)
{
    if (t == NULL)
        return false;
    return t->color;
}

// private rotation at left direction method
template
TreeNode* Tree::leftRotation(TreeNode* t)
{
    TreeNode* x = t->rightChild;
    t->rightChild = x->leftChild;
    x->leftChild = t;
    x->color = t->color;
    t->color = true;
    return x;
}

// private rotation at right direction method
template
TreeNode* Tree::rightRotation(TreeNode* t)
{
    TreeNode* x = t->leftChild;
    t->leftChild = x->rightChild;
    x->rightChild = t;
    x->color = t->color;
    t->color = true;
    return x;
}

// private flip color
template
void Tree::flipColor(TreeNode* t)
{
    t->color = true;
    t->leftChild->color = false;
    t->rightChild->color = false;
}

// private insert accomplish method
template
TreeNode* Tree::insert_ac(TreeNode* t, TreeNode*t2)
{

    if (t == NULL)
    {
        t2->color = true;
        return t2;
    }
        
         
    if (t->key > t2->key)
        t->leftChild = insert_ac(t->leftChild, t2);
    else if (t->key < t2->key)
        t->rightChild = insert_ac(t->rightChild, t2);
    else
        t->value = t2->value;

    if (isRed(t->rightChild) && !isRed(t->leftChild))
        t = leftRotation(t);
    if (isRed(t->leftChild) && isRed(t->leftChild->leftChild))
        t = rightRotation(t);
    if (isRed(t->leftChild) && isRed(t->rightChild))
        flipColor(t);
    return t;

}
#pragma endregion

#pragma region PUBLIC METHODS
// constructor
template
Tree::Tree()
{
    root = NULL;
}

// deconstructor
template
Tree::~Tree()
{
}

// public empty or not method
template
bool Tree::isempty()
{
    return root == NULL ? true : false;
}

// public insert method
template
void Tree::insert(TreeNode*t)
{

    root = insert_ac(root,t);
    root->color = false;
}

// public layer order
template
void Tree::layerOrder()
{
    std::queue*> q;
    TreeNode* currentNode = root;
    while (currentNode)
    {
        Show(currentNode);
        if (currentNode->leftChild)
            q.push(currentNode->leftChild);
        if (currentNode->rightChild)
            q.push(currentNode->rightChild);
        if (q.empty())
            break;
        currentNode = q.front();
        q.pop();
    }
}

// public show
template
void Tree::Show(TreeNode* t) const
{
    cout << t->key << ": " << t->value << "( " << (t->color ? "red" : "black") << ")" << endl;
}
#pragma endregion

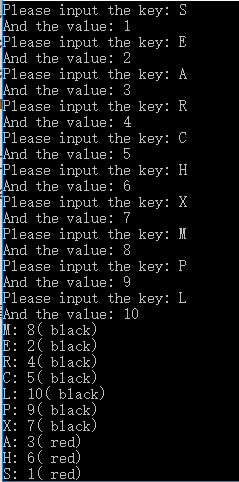
主函数通过层序遍历验证代码正确性。

#include 
#include "MyTree.h";
using namespace std;
const int NUM = 10;
int main()
{
    Tree tree;
    TreeNode temp[NUM];
    for (int i = 0; i < NUM; i++)
    {
        std::cout << "Please input the key: ";
        std::cin >> (temp[i].key);
        std::cout << "And the value: ";
        std::cin >> (temp[i].value);
        tree.insert(&temp[i]);
    }
    tree.layerOrder();
    system("pause");
    return 0;
}

打印一个有红黑分类的结果

红黑树输出结果.png

3、红黑树的删除

红黑树的删除需要借助2-3-4树来进行删除。也就是说，4-结点将会存在。并且，这种4-结点的拆分与合成是双向的。即从树根到树底，从树底到树根这两种变换都是允许的。
4-结点的表示：
a、4-结点的表示是由一个父节点及其左子结点和右子结点组成。此时，父结点与子结点的连接均为红色。
b、从树根向树底搜索/删除时，需要分解4-结点，并且将父结点与子结点的颜色进行转换。
c、进行删除后，需要对4-结点进行整合。

首先，先写出删除最小键与最大键。要找到最小键与最大键其实比较简单，由上一章所讲，最小(大)键的寻找即是一直向树的左(右)子结点进行查找，最左(右)结点即是最小(大)值。红黑树的寻找最小(大)键也是如此。但存在的问题是：若最小(大)结点是一个3-结点，那么可以直接将其左链接删除；若最小(大)结点是一个2-结点，那么删除后即为空链接，此时树的平衡就被打破了。因此，需要借助2-3-4树，来对最小(大)结点进行删除。

最小值的删除

思路：每一次向左寻找，都要保证该左结点不是2-结点。以这个为基调，不断向左寻找3-结点或者4-结点，然后再将3-结点或4-结点中最左的节点删除。(实际上，在不断向左的过程中，每一个向左的连接都可能要变为红链接)， 将最左的红链接删除后，再向上配平节点（通过旋转和颜色反转等操作）。主要的情况有：
1、根节点处，如果根节点是一个标准的二叉树，即根节点的左子结点与右子结点都是黑链接，此时，需要将三个节点的颜色都变为红色，将其写成一个4-结点。
2、根结点以及其左子结点是2-结点，其右子结点为3-结点，此时可以通过旋转操作，向右子结点借一个结点到左子结点中，使左子结点成为一个3-结点。

// private deleteMin_ac method
template
TreeNode* Tree::deleteMin_ac(TreeNode* t)
{
    if (t->leftChild == NULL)
        return NULL;
    if (!(isRed(t->leftChild)) && !(isRed(t->leftChild->leftChild)))  // 3-node judgement
        t = moveRedLeft(t);
    t->leftChild = deleteMin_ac(t->leftChild);
    return balance(t);
}

// private moveRedLeft method
template
TreeNode* Tree::moveRedLeft(TreeNode* t)
{
    flipColors(t);
    if (isRed(t->rightChild->leftChild))
    {
        t->rightChild = rightRotation(t->rightChild);
        t = leftRotation(t);
    }
    return t;
}
// private flipColors method
template
void Tree::flipColors(TreeNode* t)
{
    t->color = false;
    t->leftChild->color = true;
    t->rightChild->color = true;
}

// private balance method
template
TreeNode* Tree::balance(TreeNode* t)
{
    if (isRed(t->rightChild))                           // balance upforwards
        t = leftRotation(t);
    if (isRed(t->rightChild) && !isRed(t->leftChild))
        t = leftRotation(t);
    if (isRed(t->leftChild) && isRed(t->leftChild->leftChild))
        t = rightRotation(t);
    if (isRed(t->leftChild) && isRed(t->rightChild))
        flipColor(t);
    return t;
}

// public deleteMin method
template
void Tree::deleteMin()
{
    if (!isRed(root->leftChild) && !isRed(root->rightChild))
        root->color = true;
    root = deleteMin_ac(root);
    if (!isempty())
        root->color = false;
}

删除最大键

删除最大键的操作其实与删除最小键相类似。但它是通过建立向右的红链接找到最大键值，并对其进行删除。思路与删除最小键值是相似的，但是在逻辑上需要做一些改动。

// private deleteMax_ac method
template
TreeNode* Tree::deleteMax_ac(TreeNode *t)
{
    if (isRed(t->leftChild))
        t = rightRotation(t);
    if (t->rightChild == NULL)
        return NULL;
    if (!isRed(t->rightChild) && !isRed(t->rightChild->leftChild))
        t = moveRedRight(t);
    t->rightChild = deleteMax_ac(t->rightChild);
    return balance(t);
}


// private moveRedRight method
template
TreeNode* Tree::moveRedRight(TreeNode* t)
{
    flipColors(t);
    if (!isRed(t->leftChild->leftChild))
        t = rightRotation(t);
    return t;
}

// public deleteMax method
template
void Tree::deleteMax()
{
    if (!isRed(root->leftChild) && !isRed(root->rightChild))
        root->color = true;
    root = deleteMax_ac(root);
    if (!isempty())
        root->color = false;
}

删除红黑树中的某个键值

删除某个键值可以采用上面的删除最小、最大值的思路。
①首先需要从树根进行向下寻找键值(get()函数)
②当当前键值大于所要删除的键值时，采用“删除最小键值”的思路向左进行寻找。
③当当前键值小于所要删除的键值时，采用“删除最大键值”的思路向右进行寻找。
④当命中所要删除的键值时，按照前一章二叉树的删除方法，寻找其右子树中的最小键，将它的位置替换为最小键，再删除其右子树的最小键。
⑤通过balance函数向上配平红黑树。

// private deleteE method
template
TreeNode* Tree::deleteE(TreeNode* t, T k)
{
    if (t == NULL)
        return NULL;
    if (k < t->key)
    {
        if (!isRed(t->leftChild) && !isRed(t->leftChild->leftChild))
            t = moveRedLeft(t);
        t->leftChild = deleteE(t->leftChild, k);
    }
    else
    {
        if (isRed(t->leftChild))
            t = leftRotation(t);
        if ((t->key == k) && (t->rightChild == NULL))
            return NULL;
        if (!isRed(t->rightChild) && !isRed(t->rightChild->leftChild))
            t = moveRedRight(t);
        if (t->key == k)
        {
            t->value = get(t->rightChild, min_ac(t->rightChild)->key);
            t->key = min_ac(t->rightChild)->key;
            t->rightChild = deleteMin_ac(t->rightChild);
        }
        else
            t->rightChild = deleteE(t->rightChild, k);
    }
    return balance(t);
}

// private get method
template
int Tree::get(TreeNode* t, T k)
{
    if (t == NULL)
        return NULL;
    if (k < t->key)
        return get(t->leftChild, k);
    else if (k > t->key)
        return get(t->rightChild, k);
    else
        return t->value;
}

// private min_ac method
template
TreeNode* Tree::min_ac(TreeNode* t)
{
    if (t->leftChild == NULL)
        return t;
    return min_ac(t->leftChild);
}

// public deleteEle method
template
void Tree::deleteELE(T k)
{
    if (!isRed(root->leftChild) && !isRed(root->rightChild))
        root->color = true;
    root = deleteE(root, k);
    if (!isempty())
        root->color = false;
}

所有基于红黑树的符号表实现都能保证操作的运行时间为对数级别的。