深度学习必备数学基础 全讲解

数学基础总览

总结花书1-4章，所必备的数学基础如下

• 矩阵对角化，SVD分解与应用（神经网络加速，图像压缩）
• 逆矩阵，伪逆矩阵，最小二乘解，最小范数解
• PCA原理与推导
• 极大似然估计等估计方法
• 有约束无约束的最优化问题

矩阵对角化与SVD分解

SVD具体内容可参考之前写的博客全面理解奇异值分解，矩阵对角化的内容简述一下：矩阵B的对角化为$P^{-1}AP=B$，这里A是对角矩阵，P是标准正交矩阵。P的每一列叫做B的特征向量，A的每一个对角元素就叫做B的对应位置的特征向量所对应的特征值。关于这个更详细的描述可参考之前写的博客线性代数——特征向量与特征值。一般的矩阵不一定能对角化，但是对称矩阵一定可以对角化。
矩阵对角化后的表达式如下
$$\begin{array}{rl}A& =\left(u_1,u_2,\cdots ,u_n\right)\left(\begin{array}{ccc}{\lambda }_1& & \\ & {\lambda }_2& \\ & & {\lambda }_3\end{array}\right)\left(\begin{array}{c}{u}_1^T\\ ⋮\\ u_n^T\end{array}\right)\\ & ={\lambda }_1{u}_1{u}_1^T+{\lambda }_2{u}_2{u}_2^T+{\lambda }_3{u}_3{u}_3^T+\cdots +{\lambda }_n{u}_n{u}_n^T\end{array}$$

这个式子就可以用来做许多的事情，比如说图像的压缩，比如说特征值的选取，比如通过协方差矩阵筛选主要特征等等。

逆与伪逆和最小二乘与最小范数解

先看最小二乘的知识，可参考之前写的这篇博客最小二乘学习笔记，里面详细说明了最小二乘的知识，博客中线性回归最小二乘的公式是：
$$\beta ={\left(x^{T}x\right)}^{-1}{x}^{T}Y$$
这里的-1就是逆，${\left(x^{T}x\right)}^{-1}{x}^T$就是伪逆（想更深入了解逆的相关知识参见之前写的博客矩阵可逆性的理解与总结）。
那么最小范数解又是什么呢？由于${\left(x^{T}x\right)}^{-1}$不一定存在逆矩阵，所以就引入了最小范数解（最终解的形式其实和岭回归一致）。线性回归最小范数解的形式为
$$\beta ={\left(x^{T}x+\lambda I\right)}^{-1}{x}^{T}Y$$

这个解是通过解这个目标函数得到的

$$\mathrm{J}=\Vert xa-Y{\Vert }^2+\lambda \Vert a{\Vert }^2$$

这里的a是权重，可见这个目标函数比最小二乘的目标函数多出来了后面那一项，这一项就叫做L2正则项，在机器学习里面如果要实现权值衰减也需要添加这一项，相关内容可参考之前写的博客pytorch中的正则化方法和岭回归，Lasso回归，最小角回归以及三者对比分析。

PCA原理与推导

PCA是一种数据压缩的方法，如下图所示

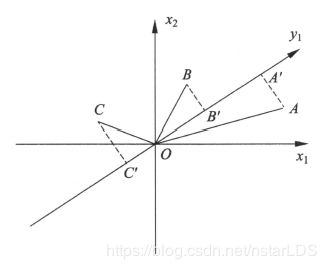
A 点需要 x,y 两个坐标来表示，假设 A 在向量 u 上面的投影点为 A’，则 A’ 仅仅需要一个参数就能表示，就是 OA’ 的长度 即 A’ 在 u 上的坐标 我们就想着用 A’ 来替换 A ，这样N个点原来要 2N 个参数，现在只需要 (N+2) 个参数 (u 也需要 2个参数)

但是此时就带来了误差，如 AA’ 和 BB’, 所以我们要能够找到这样一个方向 u, 使得所有原始点与投影点之间的误差最小，也就是找到最小重构误差。

以A点为例，假设向量AA’为e，向量OA为x，向量OA’为u（其实就叫做主方向），则
$$\begin{array}{rl}e& =x-⟨x,u⟩u\\ & =x-\left(x^{T}u\right)u;x,u\in {\mathbb{R}}^n\end{array}$$

其中
$$\Vert u\Vert =1,u^{T}u=1$$

所以得出损失函数（目标函数）为
$$\begin{array}{l}\begin{array}{rl}J& =\Vert e{\Vert }^2=e^{T}e={\left[x-\left(x^{T}u\right)u\right]}^T\left[x-\left(x^{T}u\right)u\right]\\ & =\left[x^T-\left(x^{T}u\right)u^T\right]\left[x-\left(x^{T}u\right)u\right]\\ & =x^{T}x-\left(x^{T}u\right)\left(x^{T}u\right)-\left(x^{T}u\right)\left(x^{T}u\right)+{\left(x^{T}u\right)}^2{u}^{T}u\\ & =\Vert x{\Vert }^2-{\left(x^{T}u\right)}^2-{\left(x^{T}u\right)}^2+{\left(x^{T}u\right)}^2\\ & =\Vert x{\Vert }^2-{\left(x^{T}u\right)}^2\end{array}\end{array}$$

我们目的是要让损失函数的值最小，所以也就是令
$$\begin{array}{l}\max {\left(x^{T}u\right)}^2\\ \iff \max \left(x^{T}u\right)\left(x^{T}u\right)\iff \max \left(u^{T}x\right)\left(x^{T}u\right)\\ \iff \max u^T\left(x{x}^T\right)u\end{array}$$

如果一共有N个样本，那么上式等价于
$$\begin{array}{l}\max {\sum }_{i=1}^N{u}^T\left(x_i{x}_i^T\right)u=u^T\left({\sum }_{i=1}^N{x}_i^T{x}_i\right)u,\text{ 且 }\Vert u\Vert =1\\ \max u^T(X)u,st:\Vert u\Vert =1\end{array}$$

这里就想到用拉格朗日函数来求解，等式罗列如下
$$\begin{array}{c}L(u,\lambda )=u^{T}Xu+\lambda \left(1-u^{T}u\right)\\ \frac{\partial L}{\partial u}=0\Rightarrow Xu-\lambda u=0\\ Xu=\lambda u\\ \frac{\partial L}{\partial u}=0\Rightarrow u^{T}u=1\end{array}$$

是否觉得眼熟？这个u就是对X进行特征值分解得到某一个的特征向量，并且每个特征向量都是单位向量。在这样的条件下，最后函数值为$\lambda u^{T}u$，这里$\lambda$越大越好，所以取最大特征值即可。

需要注意！上面解法的前提是默认只能有一个方向u来表示这些点，也就是说只能选取一个坐标轴作为投影方向。这样的解法没有办法解释保留多个主方向的PCA，如果需要深入了解，可参考之前写的博客主成分分析 所有知识点全解。

也就是说给定N个样本（上式的$x_i$），如果要找一个坐标轴重新投影这些点，使得和原来比起来误差最小，那么这个坐标轴的方向就是X（$X=x_i{x}_i^T$）的某个特征向量的方向。如果把所有特征向量都取过来当作一组新的坐标轴来表示这些点，那么这些点的信息不会有任何损失。如果去掉一些坐标轴甚至只保留一个坐标轴，那么这个坐标轴的方向就是最大特征值对应的特征向量的方向。

最后一定要强调的是，这里的x必须是已经经过中心化之后的x！否则上面的讨论是没有意义的。

极大似然估计

这里就不多说了，可以直接参考之前写的博客：
极大似然估计与贝叶斯估计
简单说就是，模型认为当前样本已经出现了，所以在构造的模型的时候，模型最后计算的结果应该是认为这些样本出现的概率最大。所以就对样本出现概率的乘积求最大值，从而优化模型的参数。

最优化问题

无约束最优化

一般采用梯度下降法，是标量（函数值）对矢量（多元函数的各个元）求导的问题（矢量对矢量求导就得雅各比矩阵），得到一个矢量，这个矢量就是梯度。梯度是函数值增长最快的方向，所以要找最小值就对梯度取负值，在这个负方向上更新一小步（这步迈多长就是学习率），最后要寻找的就是梯度各维都为0的点。

还可以使用牛顿法。
第一种解释是找函数一阶导的0点（找到导数的0点就是找到了极值点），来逐步逼近。
第二种解释是在某一点，采用一个二次函数来近似这个点周围的函数（为什么可以用二次函数近似可由泰勒公式证明），然后来找二次函数的最低点，最低点就是对称轴所在的位置，也就是$-\frac{b}{2a}$，最后就导出牛顿法的迭代公式$x_0-\frac{f(x_0{)}^{{}^{\prime }}}{f(x_0{)}^{{}^{\prime \prime }}}$。

拟牛顿法就是简化二阶矩阵的逆矩阵，因为要求上面迭代公式里面的二阶导在高维的情况下是很麻烦的，拟牛顿法就利用另外一个矩阵来逼近逆矩阵，从而加速计算的过程。

比较：梯度下降是一次收敛，牛顿法是二次收敛，相比而言，牛顿法的收敛速度快，但是计算复杂，同时需要在比较接近最优点的时候才能收敛，否则就可能发散。
所以两者是有点互补的，最理想的就是先用梯度下降法来逼近，然后用牛顿法来找到精确的最优点。

有约束最优化

如果如下情况的等式约束：
$$\begin{array}{c}{\max }_{x,y}f(x,y)\\ s.t.g(x,y)=0\end{array}$$

可参考这张图

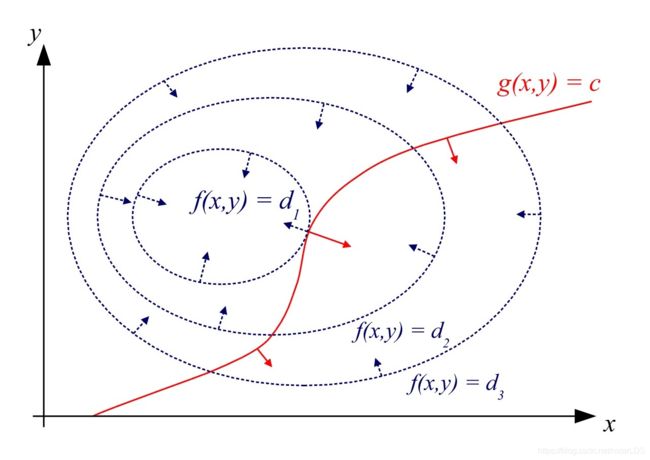
这张图说明，其实等式约束代表的就是一条直线，上图的一圈圈的椭圆虚线就是函数值的等高线，如果希望函数值越大或越小，同时x和y必须满足要在这条红色的直线上，那就只有一种情况：就是等高线和红色线相切，这时候函数值达到极值。相切就有f的梯度和g的梯度在一条直线上，所以有
$$\{\begin{array}{l}\nabla f(\mathbf{x},\mathbf{y})=\lambda \nabla g(\mathbf{x},\mathbf{y})\\ g(\mathbf{x},\mathbf{y})=c\end{array}\text{\hspace{1em}(1)}$$

引入拉格朗日函数
$$L(x,y,\lambda )=f(x,y)+\lambda g(x,y)$$

对拉格朗日函数分别求偏导，解导数为0时的解，达到的效果就和公式（1）一样。

如果是不等式约束，就不是一条线了，而是一条线划分出的空间的某个范围，这时候在前面等式约束的基础上，就要加上一个KKT条件了。什么是KKT条件？如果想深入了解可参考之前写过的博客最大熵模型与学习算法附加拉格朗日对偶性详解中拉格朗日对偶性的讲解部分。如果简单了解，就看如下条件：
$$\lambda g(x,y)=0$$

这个条件叫做互补松弛条件，可以将它近似理解成KKT条件。其意思就是，当原问题中不等式约束条件不等于0时（也就是小于0），也就是说在原问题中这个g(x, y)没有取到边界上，所以这个不等式约束是没有用的，那就要令其系数$\lambda$为0来代表这个约束没用。如果有用了，取到边界上了，这时候g(x, y)=0，$\lambda$可以取任意值，就不对$\lambda$做限制了。
总结一下就是对不起作用的约束，让$\lambda$为0。注意这里的$\lambda$是大于等于0的。