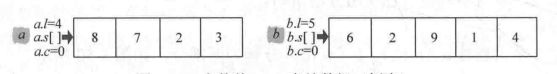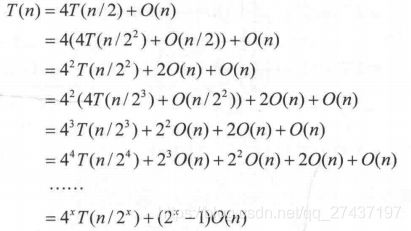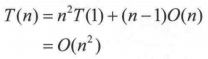分治法-大整数乘法
问题分析:
在计算机上处理一些大数据相乘时,由于计算机硬件的限制,不能直接进行相乘得到想要的结果。可以将一个大的整数乘法分而治之,将大问题变成小问题,变成简单的小数乘法再进行合并,从而解决上述问题。
当分解到只有一位数时,乘法就很简单了。
算法设计:
分解:
首先将2个大整数a(n位)、b(m位)分解为两部分:ah和al、bh和bl
ah表示大整数a的高位,al表示大整数a的低位,![]() ,ah、al为n/2位。
,ah、al为n/2位。
bh表示大整数b的高位,bl表示大整数b的低位,![]() ,bh、bl为m/2位。
,bh、bl为m/2位。
2个大整数a(n位)、b(m位)相乘转换成了4个乘法运算ah*bh、ah*bl、al*bh、al*bl,而乘数的位数变为了原来的一半。
求解子问题:
继续分解两个乘法运算,直到分解有一个乘数位1位数时停止分解,进行乘法运算并记录结果。
合并:
将计算出的结果相加并回溯,求出最终结果。
#include
#include
#include
using namespace std;
#define M 100
char sa[1000];
char sb[1000];
typedef struct _Node {
int s[M];
int l;
int c;
} Node, *pNode;
void cp(pNode src, pNode des, int st, int l) {
int i, j;
for (i = st, j = 0; i < st + l; i++, j++) {
des->s[j] = src->s[i];
}
des->l = l;
des->c = st + src->c;
}
void add(pNode pa, pNode pb, pNode ans) {
int i, cc, k, palen, pblen, len;
int ta, tb;
pNode temp;
//保证pa是高次幂
if ((pa->c < pb->c)) {
temp = pa;
pa = pb;
pb = temp;
}
ans->c = pb->c; //结果的幂取最少的幂
cc = 0;
palen = pa->l + pa->c; //pa的长度
pblen = pb->l + pb->c; //pb的长度
//选取最长的长度
if (palen > pblen)
len = palen;
else
len = pblen;
k = pa->c - pb->c;
//k是幂差,len是最长的位数
for (i = 0; i < len - ans->c; i++) {
if (i < k)
ta = 0;
else
ta = pa->s[i - k];
if (i < pb->l)
tb = pb->s[i];
else
tb = 0;
if (i >= pa->l + k)
ta = 0;
ans->s[i] = (ta + tb + cc) % 10;
cc = (ta + tb + cc) / 10;
}
if (cc)
ans->s[i++] = cc;
ans->l = i;
}
void mul(pNode pa, pNode pb, pNode ans) {
int i, cc, w;
int ma = pa->l >> 1, mb = pb->l >> 1;
Node ah, al, bh, bl;
Node t1, t2, t3, t4, z;
pNode temp;
if (!ma || !mb) {
//如果pa是一位数,则和pb交换
if (!ma) {
temp = pa;
pa = pb;
pb = temp;
}
ans->c = pa->c + pb->c;
w = pb->s[0]; //pb必为一位数
cc = 0;
for (i = 0; i < pa->l; i++) {
//pa必为2位数以上
ans->s[i] = (w * pa->s[i] + cc) % 10;
cc = (w * pa->s[i] + cc) / 10;
}
if (cc)
ans->s[i++] = cc;
ans->l = i;
return;
}
cp(pa, &ah, ma, pa->l - ma); //高位升幂
cp(pa, &al, 0, ma); //低位幂不变
cp(pb, &bh, mb, pb->l - mb);
cp(pb, &bl, 0, mb);
mul(&ah, &bh, &t1);
mul(&ah, &bl, &t2);
mul(&al, &bh, &t3);
mul(&al, &bl, &t4);
add(&t3, &t4, ans);
add(&t2, ans, &z);
add(&t1, &z, ans);
}
int main() {
Node ans, a, b;
cout << "输入大整数 a:" << endl;
cin >> sa;
cout << "输入大整数 b:" << endl;
cin >> sb;
a.l = strlen(sa);
b.l = strlen(sb);
int z = 0, i;
for (i = a.l - 1; i >= 0; i--)
a.s[z++] = sa[i] - '0';
a.c = 0;
z = 0;
for (i = b.l - 1; i >= 0; i--)
b.s[z++] = sb[i] - '0';
b.c = 0;
mul(&a, &b, &ans);
cout << "最终结果为:";
for (i = ans.l - 1; i >= 0; i--)
cout << ans.s[i];
cout << endl;
return 0;
} 代码解释:
1、将两个输入的大数,倒序存储在数组s[]中,l表示长度,c表示幂,c初始为0。
2、cp函数:将一个n位的数,分成两个n/2的数并存储,记录它的长度和次幂。
3、mul函数,不断地分解,直到有一个乘数为1位数时停止分解,进行乘法并记录结果。
4、add函数,将分解得到的数,进行相加合并。
代码流程:
初始化:将a、b倒序存储在数组a.s[],b.s[]中。
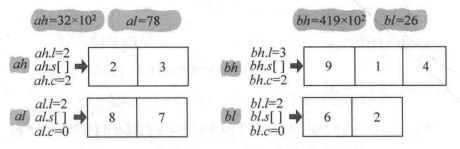
分解:cp函数:将一个n位的数,分成两个n/2的数并存储,记录它的长度和次幂。ah表示高位,al表示低位,l用来表示数的长度,c表示次幂。
转换为4次乘法运算:ah*bh,ah*bl,al*bh,al*bl:
求解子问题:
ah*bh,ah*bl,al*bh,al*bl
继续求解子问题:
上述4个乘法运算都有一个乘数为1位数,可以直接进行乘法运算。以ahh*bhh为例:
 3首先和1相乘得到3存储在下面数组的第0位,然后3和4相乘得到12,先存储12%10=2,然后存储进位12/10=1,那样结果就为倒序的321,结果的次幂是两个乘数次幂之和。
3首先和1相乘得到3存储在下面数组的第0位,然后3和4相乘得到12,先存储12%10=2,然后存储进位12/10=1,那样结果就为倒序的321,结果的次幂是两个乘数次幂之和。
4个乘法运算结果如下图:
合并:
合并子问题结果,返回给ah*bh,将上面4个乘法运算的结果加起来返回给ah*bh。
由此得到ah*bh=13408x10^4。
用同样的方法求得ah*bl=832x10^2,al*bh=32682x10^2,al*bl=2028。将这4个子问题结果加起来,合并得到原问题a*b=137433428。
算法复杂度分析:
假设两个n位大整数相乘的时间复杂度为T(n),则:
当n>1时,可以递推求解如下:
递推最终的规模为1,令n=2^x,则x=logn,那么有:
大整数乘法的时间复杂度为O(n^2)。
空间复杂度:
程序中变量占用了一些辅助空间,都是常数阶,但合并时结点数组占用的辅助空间为O(n),递归调用所使用的栈空间时O(logn)。所以,空间复杂度为O(n)。