【python3】任务分配问题
实验四:矩阵算法
一、实验目的
问题描述:N个人分配N项任务,一个人只能分配一项任务,一项任务只能分配给一个人,将一项任务分配给一个人是需要支付报酬,如何分配任务,保证支付的报酬总数最小。假设N=5,每个人工作和报酬之间的关系如下表所示,求解该问题的最优解
表1.1 任务分配
work1 work2 work3 work4 work5
person1 90 75 75 80 60
person2 35 85 55 65 48
person3 125 95 90 105 100
person4 45 110 95 105 98
person5 76 64 57 88 90
二、实验要求
(1)做好实验预习
(2)独立完成实验
(3)撰写实验报告
三、实验题目
本实验由于要求较少,只是寻求最优解,因此采用简单的方法。
四、实验环境
本文的编程环境为Ubantu16.04。
本文的编程语言为Python3.7。
五、实验分析与设计思路
本实验采用的是矩阵的方式进行计算,但是其中包含了列表的计算方法,矩阵的相乘。
主要采用的程序:
np.array([])生成一个想要的数组 包括列向量,和行向量。
b=numpy.array([b]).T 行向量转成列向量。
a.dot(b) 向量的乘法。
a*b 只是对应相乘不是矩阵的乘法。
a[[1,2],:]=a[[2,1],:] 矩阵的一二两行对调。
左乘单位行向量再乘以已知矩阵再乘以变换矩阵再乘以单位列向量。
六,程序源码
#本实验要求计算利润的最小值杠杠简单
#本次实验打算采用矩阵的方式,不懂勿扰
#np.array([])生成一个想要的数组 包括列向量,和行向量
#b=numpy.array([b]).T 行向量转成列向量
#a.dot(b) 向量的乘法
#a*b 只是对应相乘不是矩阵的乘法
#a[[1,2],:]=a[[2,1],:] 矩阵的一二两行对调
#左乘单位行向量再乘以已知矩阵再乘以变换矩阵再乘以单位列向量
#========================================================================
#智能优化算法---计算工作分配方案(原创)
#作者:Vince
#版本号:1.0
#创作日期:2018.10.31
#如需转载,请电联.
#耗时:4h
#=========================================================================
import random
import math
import numpy as np
import copy
import numpy as np
import matplotlib.pyplot as plt
class Min(object):
def __init__(self,newList = [],n=5):
self.newList = newList #初始列表工作的选择
self.diag = np.identity(5) #生成一个五维单位矩阵
self.dhxl = np.array([1,1,1,1,1]) #单位行向量
self.dlxl = np.array([[1],[1],[1],[1],[1]])#单位列向量
self.value = 0#每一次的报酬
self.bestvalue = 100000 #每一次初始种群的最佳报酬
self.bestchoice = np.identity(5) #每一次的初始种群的最佳方案
self.empty = [[-1,-1]] #禁忌表
self.n=n #人数或工作的量
self.num = (((self.n-1)+1)*4/2) #计算循环次数
self.bestdiag=np.identity(5)
def Pso(self):
self.empty = [[-1,-1]]
self.diag = self.bestdiag
self.value = self.bestvalue
i = 0
while i < 10:
index1 = random.randint(0,4) #生成初始种群需要互换的两行
index2 = random.randint(0,4)
if (index1,index2)!=self.empty[-1] and (index2,index1)!=self.empty[-1] and index1!=index2:#比对禁忌表中是否存在
self.empty.append((index1,index2))#将互换两行的行号放入禁忌表
self.diag[[index1,index2],:] = self.diag[[index2,index1],:]#将两行互换
self.value = self.Cul(self.diag)#计算报酬
if self.value < self.bestvalue:#
self.bestvalue = self.value
self.bestdiag = self.diag
self.bestchoice = self.newList*self.bestdiag
i += 1
# print(self.empty)
def Cul(self,diag):
diag = self.newList*diag
diag = self.dhxl.dot(diag)
value = diag.dot(self.dlxl)
return value
def getValue(self):#返回局部最佳值
return self.bestvalue
def getchoice(self):#返回局部最佳方案
return self.bestchoice
def main(turn):
newList = np.array([[90,75,75,80,60],[35,85,55,65,48],[125,95,90,105,100],[45,110,95,105,98],[76,64,57,88,90]])
num = 5
tbv = []
tbc = []
i=0
min = Min(newList,num)
while i<turn:
min.Pso()
value = min.getValue()
tbv.append(value)
choice = min.getchoice()
tbc.append(choice)
print('这是第%d次选择'%(i+1))
print('报酬的最小值:%d'%value)
print('最佳选择为:')
print(str(choice))
i += 1
# print('\n')
nb=copy.deepcopy(tbv)
nb.sort() #将所有的局部最佳值进行排序
i = 0
while i<turn:
if tbv[i][0] == nb[0][0]:
break
i += 1
print('全局报酬最优解:%d'%tbv[i])
print('最佳选择为:')
print(str(tbc[i]))
return tbv[i][0]
# main(10)
def psoPlot():
x = []
y = []
i=1
while i< 50:
tc = main(i)
#x轴 y轴
x.append(i)
y.append(tc)
print(i)
i += 1
#创建绘图对象,figsize参数可以指定绘图对象的宽度和高度,单位为英寸,一英寸=80px
plt.figure(figsize=(8,8))
#在当前绘图对象进行绘图(两个参数是x,y轴的数据)
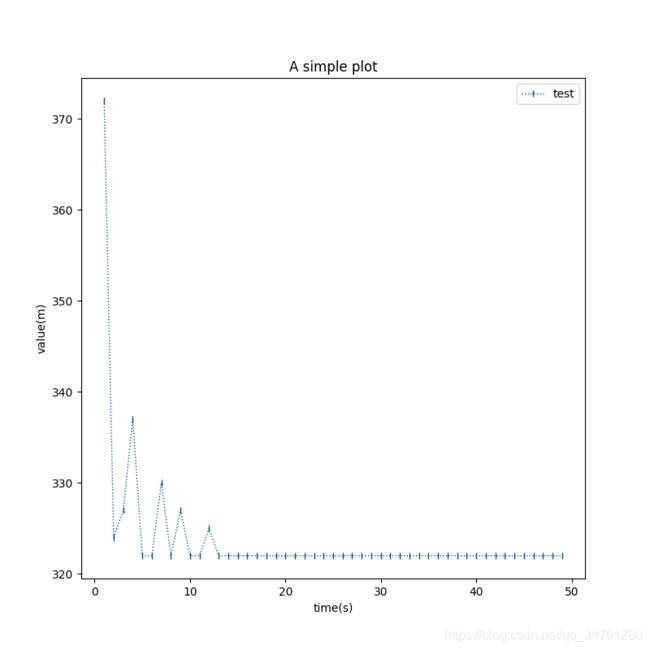
plt.plot(x, y, linewidth = '1', label = "test",color='#054E9F', linestyle=':', marker='|')
plt.xlabel("time(s)") #X轴标签
plt.ylabel("value(m)") #Y轴标签
plt.title("A simple plot") #标题
#保存图象
# plt.savefig("easyplot.png")
plt.legend()
plt.show()
psoPlot()