美丽而巧妙的定理——莫利定理
内容
莫利定理(Morley’s theorem),也称为莫雷角三分线定理。将三角形的三个内角三等分,靠近某边的两条三分角线相交得到一个交点,则这样的三个交点可以构成一个正三角形。这个三角形常被称作莫利正三角形。
上图!
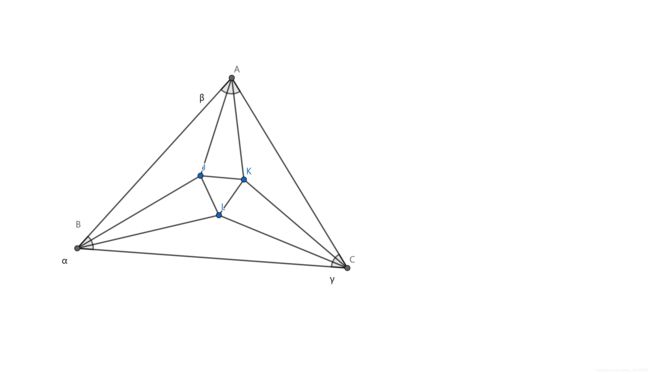
https://www.geogebra.org/graphing/hsexyt4d
证明
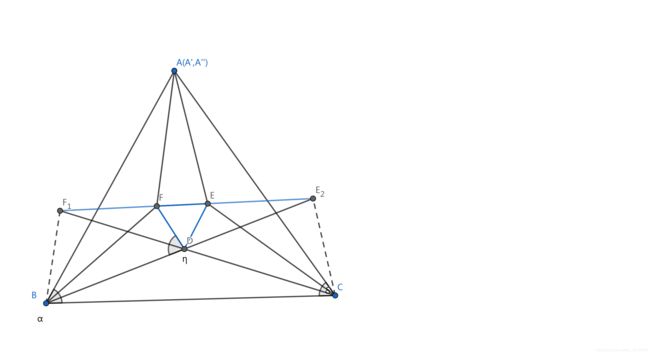
如图 , 在任意 △ A B C △ABC △ABC 内部构造 △ B D C △BDC △BDC, 使 ∠ D B C = ∠ B 3 , ∠ D C B = ∠ C 3 ∠DB C =∠B3, ∠D CB =\large\frac{∠C}{3} ∠DBC=∠B3,∠DCB=3∠C, 又作 △ B D F △BDF △BDF , 使 ∠ D B F = ∠ B 3 , ∠ B D F = 60 ° + ∠ C 3 ∠DBF=\large\frac{∠B}{3}, ∠BDF=60°+\large\frac{∠C}{3} ∠DBF=3∠B,∠BDF=60°+3∠C, 使 D F DF DF 交 B F BF BF于 F F F,作正 △ D F E △DFE △DFE , 则 ∠ E D C = 60 ° + ∠ B 3 ∠EDC= 60°+\large\frac{∠B}{3} ∠EDC=60°+3∠B. 又连结 E C EC EC, 分别延长 B D BD BD 与 C D CD CD 交 E F EF EF 于点 E 2 E_2 E2、 F 1 F_1 F1,
则 ∠ F 1 = ∠ E D C − ∠ D E F 1 = ∠ B 3 ∠F_1=∠EDC-∠DEF_1=\large\frac{∠B}{3} ∠F1=∠EDC−∠DEF1=3∠B
同理 ∠ E 2 = ∠ C 3 ∠E_2 =\large\frac{∠C}{3} ∠E2=3∠C.
显然 B , C , E 2 , F 1 B,C,E_2,F_1 B,C,E2,F1 共圆;
点 B , D , F , F 1 B,D,F,F_1 B,D,F,F1 共圆.
∴ ∠ E 2 C F 1 = ∠ E 2 B F 1 = ∠ D F E = ∠ D E F ∴ ∠E_2CF_1=∠E_2BF_1=∠DFE=∠DEF ∴∠E2CF1=∠E2BF1=∠DFE=∠DEF
故 D , C , E 2 , E D,C,E_2,E D,C,E2,E共圆,
∴ ∠ D C E = ∠ E 2 = ∠ C 3 ∴ ∠DCE=∠E 2 =\large\frac{∠C}{3} ∴∠DCE=∠E2=3∠C
故 △ D E C △D EC △DEC 中, ∠ D E C = 60 ° + ∠ A 3 ∠D EC = 60°+\large\frac{∠A}{3} ∠DEC=60°+3∠A
又作 ∠ C E A ′ = 120 ° + ∠ B 3 ∠CEA ′= 120°+∠B3 ∠CEA′=120°+∠B3交 C A CA CA 于点 A ′ A^′ A′
则 ∠ E A ′ C = ∠ A 3 ∠EA^′C =\large\frac{∠A}{3} ∠EA′C=3∠A, ∠ A ′ E F = 60 ° + ∠ C 3 ∠A^′EF=60°+\large\frac{∠C}{3} ∠A′EF=60°+3∠C.又连结 F A ′ FA^′ FA′并延长交 B A BA BA 于点 A ″ A^{″} A″, 则同理可证: ∠ F A ′ E = ∠ A 3 ∠FA^′E =\large\frac{∠A}{3} ∠FA′E=3∠A
∠ A ″ F E = ∠ A ′ F E = 60 ° + ∠ B 3 ∠A^{″}F E = ∠A ′F E = 60°+\large\frac{∠B}{3} ∠A″FE=∠A′FE=60°+3∠B
从而 ∠ A ″ F B = 120 ° + ∠ C 3 , ∠ B A ″ F = ∠ A 3 ∠A^{″}FB = 120°+\large\frac{∠C}{3}, ∠BA^{″}F =\large\frac{∠A}{3} ∠A″FB=120°+3∠C,∠BA″F=3∠A
又连结 A ″ E A^{″}E A″E , 则又同理可证 ∠ F A ″ E = ∠ A 3 ∠FA ″E =\large\frac{∠A}{3} ∠FA″E=3∠A
∴ ∠ F A ′ E = ∠ F A ″ E = ∠ A 3 ∴ ∠FA^′E=∠FA^″E=\large\frac{∠A}{3} ∴∠FA′E=∠FA″E=3∠A
∴ ∴ ∴点 A ′ A^′ A′与 A ″ A^{″} A″必重合于点 A A A , 则易知 ∠ E A C = ∠ F A E = ∠ F A B = ∠ A 3 ∠EAC=∠FAE=∠FAB=\large\frac{∠A}3 ∠EAC=∠FAE=∠FAB=3∠A
故正 △ D E F △DEF △DEF 是 △ A B C △ABC △ABC 的内角莫来三角形
证毕.
注:
证明很初等,方法不简单。