斐波那契查找

1. 问题描述

       我们知道，对于有序数据序列进行查找，二分查找法性能是相当好的，时间效率达到O(log2n)，但该算法其实还有些可以进行改进的地方。普通的折半查找直接通过折半的方式对有序数据序列进行分割，这种方法实际上不是十分有效。对于大多数的有序数据序列，通常分布都是比较均匀的，可以通过斐波那契数列对有序表进行分割。斐波那契查找方法也称为黄金分割法，其平均性能比折半查找要好。

2. 基本要求

（1）设计斐波那契查找算法；

（2）与普通的折半查找算法进行比较。

3. 问题分析

斐波那契查找主要用到了斐波那契数列F(1)=1，F(2)=1,····, F(n)=f(n-1)+F(n-2)（n>=2)的一条性质：前一个数除以相邻的后一个数，比值无限接近黄金比例值(0.618)。

斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个大于等于查找表中元素个数的数F[n]，将原查找表扩展为长度为F[n](如果要补充元素，则补充重复最后一个元素，直到满足F[n]个元素)，完成后进行斐波那契分割，即F[n]个元素分割为前半部分F[n-1]个元素，后半部分F[n-2]个元素，找出要查找的元素在那一部分并递归，直到找到。使用斐波那契查找的条件是：(1)数据必须采用顺序存储结构；(2)数据必须有序。

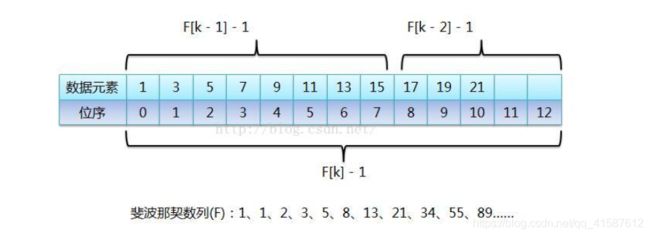
比如这里的89，把它想象成整个有序表的元素个数，而89是由前面的两个斐波那契数34和55相加之后的和，也就是说把元素个数为89的有序表分成由前55个数据元素组成的前半段和由后34个数据元素组成的后半段，那么前半段元素个数和整个有序表长度的比值就接近黄金比值0.618，假如要查找的元素在前半段，那么继续按照斐波那契数列来看，55 = 34 + 21，所以继续把前半段分成前34个数据元素的前半段和后21个元素的后半段，继续查找，如此反复，直到查找成功或失败，这样就把斐波那契数列应用到查找算法中了。

从图中可以看出，当有序表的元素个数不是斐波那契数列中的某个数字时，需要把有序表的元素个数长度补齐，让它成为斐波那契数列中的一个数值，当然把原有序表截断肯定是不可能的，不然还怎么查找。然后图中标识每次取斐波那契数列中的某个值时(F[k])，都会进行-1操作，这是因为有序表数组位序从0开始的，纯粹是为了迎合位序从0开始。

问题没有设置其余的限制条件。

所设计的系统需要输入的数据类型为整型(int型)，输出值的有效范围取决于编译器，输入形式为：用户根据系统提出的问题输入相应操作的整数，并按回车表示结束输入。

该系统的输出数据类型为整型或字符串型，输出的形式为：命令行交互界面会呈现编译器在后台的计算结果。

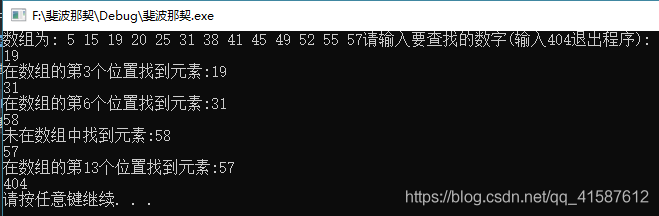
准备的测试数据有：19、31、57、58、404。

4.  概要设计

斐波那契查找的抽象数据类型定义：

ADT Fibonacci_Search

DataModel

元素从大到小或从小到大顺序存储在一位数组中。

Operation

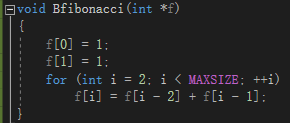
Bfibonacci

    输入：斐波那契数列f[MAXSIZE]

    功能：给斐波那契数列赋值

    输出：斐波那契数列f

fibonacci_search

        输入：要查找的数组a,要查找的关键字key,要查找的数组长度n

        功能：定位要查找的关键字

        输出：关键字在数组中的位置

endADT

 

算法用伪代码表描述如下:

算法：Fibonacci_search

输入：要查找的数组a,要查找的关键字k,要查找的数组长度n

输出：关键字在数组中的位置

        1. 设置初始查找区间 low=1；high=F(k)-1；            

        2. 计算当前查找区间的表长；计算分割点距区间低端的偏移量；

              F=F(k)-1；f=F(k-1)-1；

        3. 当查找区间存在，执行下列操作：

            3.1 取查找区间的分割点mid=low+f；

            3.2 将r[mid]与待查值k比较，有以下三种情况：

                 ⑴ 若k

                       p=f；f=F-f-1；   //计算分割点距该查找区间低端的偏移量

                       F=p；           //计算左半区间的表长

                       high=mid-1；     //调整查找区间的高端位置

                   ⑵ 若k>r[mid]，则查找在右半区间继续进行；

                        F=F-f-1；        //计算右半区间的表长

                        f=f-F-1；         //计算分割点距该查找区间低端的偏移量

                        low=mid+1；      //调整查找区间的低端位置

                    ⑶ 若k=r[mid]，则查找成功，返回记录在表中位置mid；

            4. 退出循环，说明查找区间已不存在，返回查找失败标志0；

5.  编码实现与静态检测

       斐波那契数列还是很好实现的，但斐波那契查找废了很大功夫去理解和实现。

       如果要查找的记录在右侧，则左侧的数据都不用再判断了，不断反复进行下去，对处于当中的大部分数据，其工作效率要高一些。所以尽管斐波那契查找的时间复杂度和折半查找一样也为O(logn)，但就平均性能来说，斐波那契查找要优于折半查找。可惜如果是最坏的情况，比如这里key=1，那么始终都处于左侧在查找，则查找效率低于折半查找。

       还有关键一点，折半查找是进行加法与除法运算的（mid=(low+high)/2），插值查找则进行更复杂的四则运算（mid = low +(high - low)*((key - a[low])/(a[high]- a[low]))），而斐波那契查找只进行最简单的加减法运算（mid = low + F[k-1] - 1），在海量数据的查找过程中，这种细微的差别可能会影响最终的效率。

6.  上机调试与测试数据

#include 
using namespace std;
#define MAXSIZE 13
void Bfibonacci(int *f)
{
	f[0] = 1;
	f[1] = 1;
	for (int i = 2; i < MAXSIZE; ++i)
		f[i] = f[i - 2] + f[i - 1];
}
int fibonacci_search(int *a, int key, int n)
{
	int low = 0, high = n - 1;
	int mid = 0;
	int k = 0;
	int F[MAXSIZE];
	Bfibonacci(F);
	while (n > F[k] - 1) //计算出n在斐波那契中的数列
		++k;
	int  * temp;//将数组a扩展到F[k]-1的长度
	temp = new int[F[k] - 1];
	memcpy(temp, a, n * sizeof(int));
	for (int i = n; i < F[k] - 1; ++i) //把数组补全
		temp[i] = a[high];
	while (low <= high)
	{
		mid = low + F[k - 1] - 1;  //根据斐波那契数列进行黄金分割
		if (temp[mid] > key)
		{
			high = mid - 1;
			k -= 1;
		}
		else if (temp[mid] < key)
		{
			low = mid + 1;
			k -= 2;
		}
		else {
			if (mid <= high) //如果为真则找到相应的位置
				return mid;
			else
				return n-1;
		}
	}
	delete [] temp;
	return -1;
}
int main()
{
	int a[] = { 5,15,19,20,25,31,38,41,45,49,52,55,57 };
	cout << "数组为:";
	for (int i = 0; i < sizeof(a) / sizeof(int); i++){cout<<" "<> k) {
		int pos = fibonacci_search(a, k, sizeof(a) / sizeof(int));
		if (pos != -1)
			cout << "在数组的第" << pos + 1 << "个位置找到元素:" << k << endl;
		else if (k == 404)break;
		else
			cout << "未在数组中找到元素:" << k << endl;
	}
	system("pause");
	return 0;
}