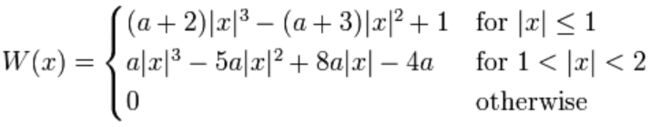Python实现双线性插值、最近邻插值、三次内插法

Python实现双线性插值、最近邻插值、三次内插法
一、最近邻插值法放大图像
最近邻插值法在放大图像时补充的像素是最近邻的像素的值。由于方法简单，所以处理速度很快，但是放大图像画质劣化明显，常常含有锯齿边缘。
原理如下：

二、双线性插值
在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。
原理图：

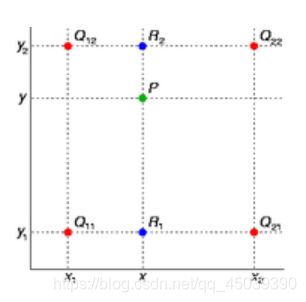
假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。那么此时可以得到未知函数 f 在点 P = (x, y) 的值。
（1）首先在 x 方向进行线性插值：

（2）在 y 方向进行线性插值：

（3）综合起来即为双线性插值最后结果：

图像双线性插值只会用相邻的4个点，上述公式的分母都是1。源图像和目标图像几何中心的对齐：
SrcX=(dstX+0.5) (srcWidth/dstWidth) -0.5
SrcY=(dstY+0.5) * (srcHeight/dstHeight)-0.5，*

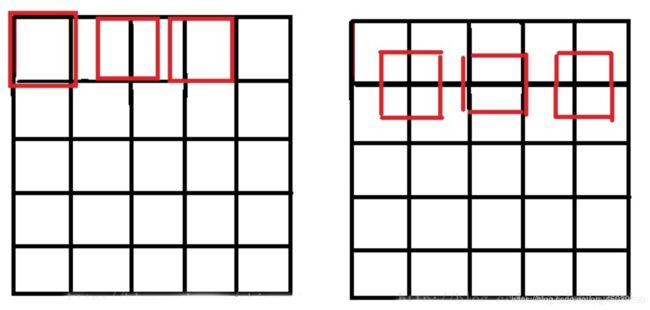
源图像和目标图像的原点（0，0）均选择左上角，然后根据插值公式计算目标图像每点像素，假设你需要将一幅5x5的图像缩小成3x3，那么源图像和目标图像各个像素之间的对应关系如下。如果没有这个中心对齐，根据基本公式去算，就会得到左边这样的结果；而用了对齐，就会得到右边的结果：

三、双三次插值
双三次插值又称立方卷积插值。三次卷积插值是一种更加复杂的插值方式。该算法利用待采样点周围16个点的灰度值作三次插值，不仅考虑到4 个直接相邻点的灰度影响，而且考虑到各邻点间灰度值变化率的影响。三次运算可以得到更接近高分辨率图像的放大效果，但也导致了运算量的急剧增加。

构造函数如下：

函数形状如下：

三次函数的运算公式：

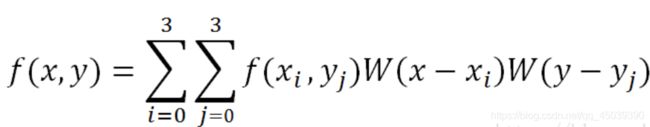
Python实现双线性插值、最近邻插值、三次内插法代码如下：

from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
import math

def NN_interpolation(img,dstH,dstW):
    scrH,scrW,_=img.shape
    retimg=np.zeros((dstH,dstW,3),dtype=np.uint8)
    for i in range(dstH):
        for j in range(dstW):
            scrx=round((i+1)*(scrH/dstH))
            scry=round((j+1)*(scrW/dstW))
            retimg[i,j]=img[scrx-1,scry-1]
    return retimg

def BiLinear_interpolation(img,dstH,dstW):
    scrH,scrW,_=img.shape
    img=np.pad(img,((0,1),(0,1),(0,0)),'constant')
    retimg=np.zeros((dstH,dstW,3),dtype=np.uint8)
    for i in range(dstH):
        for j in range(dstW):
            scrx=(i+1)*(scrH/dstH)-1
            scry=(j+1)*(scrW/dstW)-1
            x=math.floor(scrx)
            y=math.floor(scry)
            u=scrx-x
            v=scry-y
            retimg[i,j]=(1-u)*(1-v)*img[x,y]+u*(1-v)*img[x+1,y]+(1-u)*v*img[x,y+1]+u*v*img[x+1,y+1]
    return retimg

def BiBubic(x):
    x=abs(x)
    if x<=1:
        return 1-2*(x**2)+(x**3)
    elif x<2:
        return 4-8*x+5*(x**2)-(x**3)
    else:
        return 0

def BiCubic_interpolation(img,dstH,dstW):
    scrH,scrW,_=img.shape
    #img=np.pad(img,((1,3),(1,3),(0,0)),'constant')
    retimg=np.zeros((dstH,dstW,3),dtype=np.uint8)
    for i in range(dstH):
        for j in range(dstW):
            scrx=i*(scrH/dstH)
            scry=j*(scrW/dstW)
            x=math.floor(scrx)
            y=math.floor(scry)
            u=scrx-x
            v=scry-y
            tmp=0
            for ii in range(-1,2):
                for jj in range(-1,2):
                    if x+ii<0 or y+jj<0 or x+ii>=scrH or y+jj>=scrW:
                        continue
                    tmp+=img[x+ii,y+jj]*BiBubic(ii-u)*BiBubic(jj-v)
            retimg[i,j]=np.clip(tmp,0,255)
    return retimg



im_path='G:/1.png'
image=np.array(Image.open(im_path))

image1=NN_interpolation(image,image.shape[0]*2,image.shape[1]*2)
image1=Image.fromarray(image1.astype('uint8')).convert('RGB')
image1.save('G:/pika2.png')

image2=BiLinear_interpolation(image,image.shape[0]*2,image.shape[1]*2)
image2=Image.fromarray(image2.astype('uint8')).convert('RGB')
image2.save('G:/pika3.png')

image3=BiCubic_interpolation(image,image.shape[0]*2,image.shape[1]*2)
image3=Image.fromarray(image3.astype('uint8')).convert('RGB')
image3.save('G:/pika4.png')

结果如下：