变分推断之高斯混合模型(案例及代码)
本文作者:合肥工业大学 管理学院 钱洋 email:[email protected] 内容可能有不到之处,欢迎交流。
未经本人允许禁止转载。
案例来源
本博客讲解的案例来源于Journal of the American Statistical Association期刊(顶刊)上的内容:
Blei D M, Kucukelbir A, McAuliffe J D. Variational inference: A review for statisticians[J]. Journal of the American Statistical Association, 2017, 112(518): 859-877.
高斯混合模型(Mixture of Gaussians model,GMM)
在之前的一篇博客中,已经介绍了变分推断的基本原理,下面将以高斯混合模型为例,推导变分推断的公式,并给出了CAVI算法流程。同时将使用python3实现这个小案例。
下图为为高斯混合模型的生成过程:

其中, x i x_{i} xi便是一个样本数据,共有 n n n个样本,并且这 n n n个样本是从 K K K个独立的高斯分布中抽的, μ k \mu _{k} μk为每个高斯分布的均值, c i c_{i} ci表示 x i x_{i} xi样本对应的哪个高斯分布,其服从一个多项式分布。
从上图中的生成过程可以发现,这里需要估计的隐变量是 μ \mu μ和 c c c。
基于贝叶斯定理,可以计算得到参数和样本的联合概率分布:
 )
)
这个公式很容易理解,不过过多介绍。
变分推断
假设变分参数为: m = ( m 1 , … , m K ) , s 2 = ( s 1 2 , … , s K 2 ) , φ = ( φ 1 , … , φ n ) m=(m_1,\ldots,m_K),s^2=(s_1^2,\ldots,s_K^2),\varphi=(\varphi_1,\ldots,\varphi_n) m=(m1,…,mK),s2=(s12,…,sK2),φ=(φ1,…,φn),其中第一个和第二个是均值 μ k \mu _{k} μk对应的两个变量,第三个参数为类别 c i c_{i} ci对应的变量。这三个参数决定了变分分布 q q q.

下界ELBO计算
在变分推断中,重要的是计算下界ELBO:

在作者的原始论文中,只给了这个公式,但在写程序的时候,还需要将这个公式对应的详细内容给表达出来,如下图所示:

在写程序的时候,需要用到这个公式。
类别参数 φ \varphi φ更新
更新类别参数 φ \varphi φ时,需要用到下面的公式:

其中第一项为:
![]()
第二项为:

基于此,可以计算对数似然的期望:
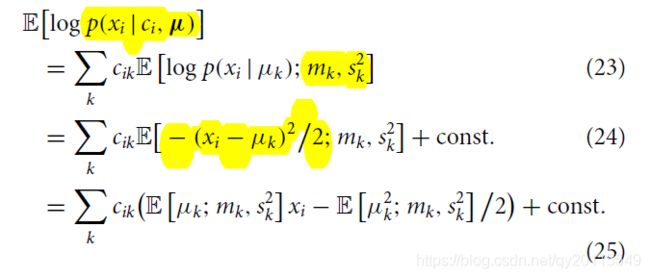
最终,我们可以使用下面公式更新类别参数:
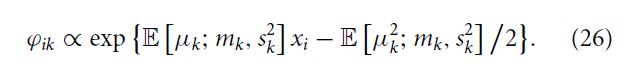
在原文中,作者只给了这个公式,但在编写程序时,需要将期望给求出来,以下是我继续推导的:

均值对应的参数的更新
下面便是 m k m_k mk以及 m k , s k 2 m_k,s_k^2 mk,sk2的更新。

取对数为:
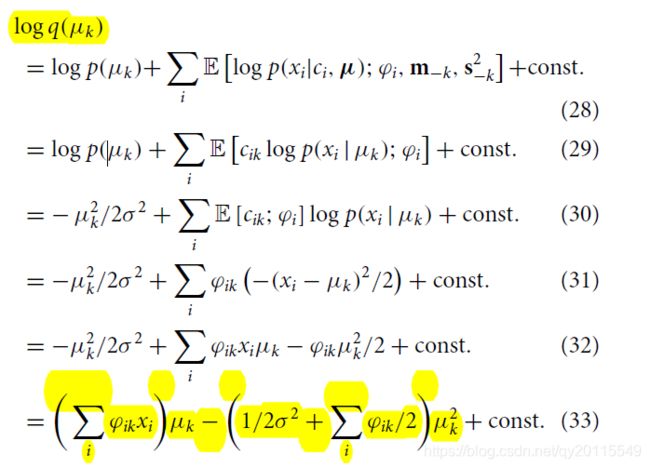
基于指数家族的性质,可以得到变分参数的更新公式,如下所示:

完整的算法流程
程序
基于上面的计算公式以及算法流程,下面来写算法程序。以下将以python3进行实现。
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
class gmm():
def __init__(self, data, num_clusters, sigma=1):
'''initialization
model parameters(m,s2,phi)--need update
'''
self.data = data
self.K = num_clusters
self.n = data.shape[0]
self.sigma = sigma
self.phi = np.random.random([self.n,self.K]) # phi(matrix n*k)
self.m = np.random.randint(np.min(data), np.max(data), self.K).astype(float) # m(matrix 1*k)
self.s2 = np.random.random(self.K) # s2(matrix 1*k)
def compute_elbo(self):
'''calculate ELOB '''
p1 = -np.sum((self.m**2 + self.s2) / (2 * self.sigma**2))
p2 = (-0.5 * np.add.outer(self.data**2, self.m**2 + self.s2) + np.outer(self.data, self.m))*(self.phi)
p3 = -np.sum(np.log(self.phi))
p4 = np.sum(0.5 * np.sum(np.log(self.s2)))
elbo_c = p1 + np.sum(p2) + p3 + p4
return elbo_c
def update_bycavi(self):
'''update (m,s2,phi)'''
# phi update
e = np.outer(self.data, self.m) + (-0.5 * (self.m**2 + self.s2))[np.newaxis, :] #[np.newaxis, :] is to matrix
self.phi = np.exp(e) / np.sum(np.exp(e), axis=1)[:, np.newaxis] #normalization K*N matrix
#m update
self.m = np.sum(self.data[:, np.newaxis] * self.phi, axis=0)/(1.0 / self.sigma**2 + np.sum(self.phi, axis=0))
# s2 update
self.s2 = 1.0 / (1.0 / self.sigma**2 + np.sum(self.phi, axis = 0))
def trainmodel(self, epsilon, iters):
'''train model
epsilon: epsilon-convergence
iters: iteration number
'''
elbo = []
elbo.append(self.compute_elbo())
# use cavi to update elbo until epsilon-convergence
for i in range(iters):
self.update_bycavi()
elbo.append(self.compute_elbo())
print("elbo is: ", elbo[i])
if np.abs(elbo[-1] - elbo[-2]) <= epsilon:
print("iter of convergence:",i)
break
return elbo
def plot(self,size):
sns.set_style("whitegrid")
for i in range(int(self.n/size)):
sns.distplot(data[size*i : (i+1)*size], rug=True)
x = np.linspace(self.m[i] - 3*self.sigma, self.m[i] + 3*self.sigma, 100)
plt.plot(x,mlab.normpdf(x, self.m[i], self.sigma),color='black')
plt.show()
if __name__ == "__main__":
# generate data
number = 1000
clusters = 5
mu = np.array([1, 5, 7, 9, 15])
data = []
# x-N(Mu,1)
for i in range(clusters):
data.append(np.random.normal(mu[i], 1, number))
# concatenate data
data = np.concatenate(np.array(data))
model = gmm(data, clusters)
model.trainmodel(1e-3, 1000)
print("converged_means:", sorted(model.m))
model.plot(number)
执行该程序,控制台输出的结果为:
参考论文
Blei D M, Kucukelbir A, McAuliffe J D. Variational inference: A review for statisticians[J]. Journal of the American Statistical Association, 2017, 112(518): 859-877.


