Apriltag使用之二：方位估计(定位)

Apriltag中计算的Homography

首先，在进行apriltag码检测时，如果检测到会一并计算出图像上apriltag码四个角点对应的homography矩阵，这个homography将这些点映射到到标准的(-1，1),(1,1),(1,-1),(-1,-1)顶点。在上面的示例一中，由homography和apriltag角点为:

H = [ 3.3831e-01     7.066e-01      -1.8602e+00
     -5.1398e-01     1.6081e-01     -1.8558e+00
      5.1039e-04    -7.7972e-05     -8.6540e-03]
%% 角点的齐次坐标
p1= [319.6915 165.3677 1.00]'
p2= [276.2611 313.7463 1.00]'
p3= [99.1906 268.6764 1.00]'
p4= [161.4450 127.7792 1.00]'

我们可以验证：

inv(H)*p1 = [ 110.05  110.05 -110.05]'  = [-1 -1  1]
inv(H)*P2 = [-123.98  123.98 -123.98]'  = [ 1 -1  1]
inv(H)*p3 = [-121.63 -121.63 -121.63]'  = [ 1  1  1]
inv(H)*p4 = [ 108.20 -108.20 -108.20]'  = [-1  1  1]

这里inv(H)是将相机图像上apriltag码角点映射到(-1，1),(1,1),(1,-1),(-1,-1)的homography。

Apriltag中的相机外参估计方法

通过给定相机的内参K，就可以利用homography对相机相对于apriltag码的方位进行估计。下面通过分析Apriltag的源码，阐述一下利用homography估计相机方位的方法。Apriltag中使用的方法属于技巧性的，

假设相机的内参矩阵为：
$$\mathbf{K}=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$
那么相机的投影矩阵就为$\mathbf{P}=\mathbf{K}[\mathbf{R}|\mathbf{t}]$，空间上的点$\mathbf{X}$通过该矩阵变为图像上的像素点$\mathbf{x}=\mathbf{P}\mathbf{X}$。
同时，我们设定Apriltag码所在的平面是在X-Y平面上($Z=0$)，其中心为坐标原点。那么有：
$$\mathbf{x}=\mathbf{K}[\mathbf{R}|\mathbf{t}]\left[\begin{array}{c}X\\ Y\\ 0\\ 1\end{array}\right]$$
因此我们可以将其中$\mathbf{R}$的第三列去掉，得到
$$\mathbf{x}=\mathbf{K}[{\mathbf{r}}_0{\mathbf{r}}_1\mathbf{t}]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]$$
其中${\mathbf{r}}_0,{\mathbf{r}}_1$是$\mathbf{R}$的第一二列。

实际上$\mathbf{K}[{\mathbf{r}}_0{\mathbf{r}}_1\mathbf{t}]$就构成了空间平面上点到图像上点的homography。那么就有一个疑问，apriltag中计算的homography不是将apriltag码的角点映射到单位方形的吗？ 是的，我们可以假想，将空间平面上的ariltag码缩小成单位方形，其实对相机的方向并没有影响，只对位置有影响。令
$$\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]=\left[\begin{array}{ccc}\lambda & 0& 0\\ 0& \lambda & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}^{\prime }\\ Y^{\prime }\\ 1\end{array}\right]$$
其中$[X,Y,1{]}^{\prime }$为缩放后的单位方形的角点。因此有：
$$\mathbf{x}=\mathbf{K}[{\mathbf{r}}_0{\mathbf{r}}_1\mathbf{t}]\left[\begin{array}{ccc}\lambda & 0& 0\\ 0& \lambda & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}^{\prime }\\ Y^{\prime }\\ 1\end{array}\right]$$
那么我们可以令$\mathbf{K}[\lambda {\mathbf{r}}_0\lambda {\mathbf{r}}_1\mathbf{t}]=\mathbf{K}[{\mathbf{r}}_0^{\prime }{\mathbf{r}}_1^{\prime }\mathbf{t}]$为apriltag计算出的${\mathbf{H}}^{\prime }$。
就有如下分解等式：
$$\begin{array}{r}{f}_x{r}_{00}^{\prime }+c_x{r}_{20}^{\prime }=h_{00}\\ f_x{r}_{01}^{\prime }+c_x{r}_{21}^{\prime }=h_{01}\\ f_x{t}_x+c_x{t}_z=h_{02}\\ f_y{r}_{10}^{\prime }+c_y{r}_{20}^{\prime }=h_{10}\\ f_y{r}_{11}^{\prime }+c_y{r}_{21}^{\prime }=h_{11}\\ f_y{t}_y+c_y{t}_z=h_{12}\\ r_{20}^{\prime }=h_{20}\\ r_{21}^{\prime }=h_{21}\\ t_z=h_{22}\end{array}$$

通过上式便可以解出${\mathbf{r}}_0^{\prime }$、${\mathbf{r}}_1^{\prime }$和$\mathbf{t}$。由于${\mathbf{H}}^{\prime }$的各列本身都是非单位化的，因此计算出的${\mathbf{r}}_0^{\prime }$和${\mathbf{r}}_1^{\prime }$就需要进行单位化处理。apriltag源码中是这样做的：
$${\mathbf{r}}_0^{\prime \prime }=\frac{{\mathbf{r}}_0^{\prime }}{\sqrt{||{\mathbf{r}}_0^{\prime }||||{\mathbf{r}}_1^{\prime }||}},{\mathbf{r}}_1^{\prime \prime }=\frac{{\mathbf{r}}_1^{\prime }}{\sqrt{||{\mathbf{r}}_0^{\prime }||||{\mathbf{r}}_1^{\prime }||}},t^{\prime }=\frac{\mathbf{t}}{\sqrt{||{\mathbf{r}}_0^{\prime }||||{\mathbf{r}}_1^{\prime }||}}$$
至于为什么$\mathbf{t}$也要做除法，其实这是符合实际的。从另一个角度看，因为有$[{\mathbf{r}}_0^{\prime }{\mathbf{r}}_1^{\prime }\mathbf{t}]={\mathbf{K}}^{-1}{\mathbf{H}}^{\prime }$，当我们知道${\mathbf{K}}^{-1}{\mathbf{H}}^{\prime }$，就可以使得${\mathbf{K}}^{-1}{\mathbf{H}}^{\prime }$的前两列单位化来得到${\mathbf{r}}_0^{\prime }$和${\mathbf{r}}_1^{\prime }$。假如要除以某个数来实现单位化，那么${\mathbf{K}}^{-1}{\mathbf{H}}^{\prime }$的第三列显示也要同时除以该数才能保持正确性。

到此我们应该清楚，单位化后${\mathbf{r}}_0,{\mathbf{r}}_1$和${\mathbf{r}}_0^{\prime },{\mathbf{r}}_1^{\prime }$是一样的，只有$\mathbf{t}$和${\mathbf{t}}^{\prime }$的不同。对于在相机图像上同一个apriltag码，$\mathbf{t}$表示相机到$\mathbf{R}$表示方向上实际大小aprilta码的距离，${\mathbf{t}}^{\prime }$则表示相机到同一方向上实际大小为单位方形的apriltag码的距离。因为是对同一个Apriltag方形在$\mathbf{t}$方向上的比例缩放，所以如果知道实际apriltag码的尺寸就可以通过比例计算出相机到实际apriltag码的距离。若apriltag码的宽度为$w$，那么相机到实际apriltag码的距离就为$\mathbf{t}=w{\mathbf{t}}^{\prime }$。

apriltag中还将$\mathbf{R}$矩阵进行SVD分解来进一步提高R的准确性。因为除以$\sqrt{||{\mathbf{r}}_0^{\prime }||||{\mathbf{r}}_1^{\prime }||}$并不一定会使得${\mathbf{r}}_0,{\mathbf{r}}_1$是精确地单位化的，只是使得它们非常接近单位化。我们令$\mathbf{R}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathbf{T}}$，然后令${\mathbf{R}}^{\prime }=\mathbf{U}{\mathbf{V}}^{\mathbf{T}}$即可。这是因为精确的$\mathbf{R}$是单位正交矩阵，可以证明（利用$\mathbf{R}{\mathbf{R}}^{\mathbf{T}}=\mathbf{I}$）分解中$\mathbf{\Sigma }=\mathbf{I}$

到此，apriltag计算出旋转矩阵$\mathbf{R}$和位置${\mathbf{t}}^{\prime }$。然后返回$4\times 4$矩阵：
$$\mathbf{M}=\left[\begin{array}{cc}\mathbf{R}& {\mathbf{t}}^{\prime }\\ 0& 1\end{array}\right]$$
注意Apriltag功能包输出的是${\mathbf{t}}^{\prime }$，要获得实际apriltag码的位置$\mathbf{t}$还需要自行进行上述的比例缩放。

在图像上标记Apriltag码的方向

得到了R和t后，相机的投影矩阵为$\mathbf{P}=\mathbf{K}[{\mathbf{R}}^{\mathbf{T}}|-\mathbf{t}]$。

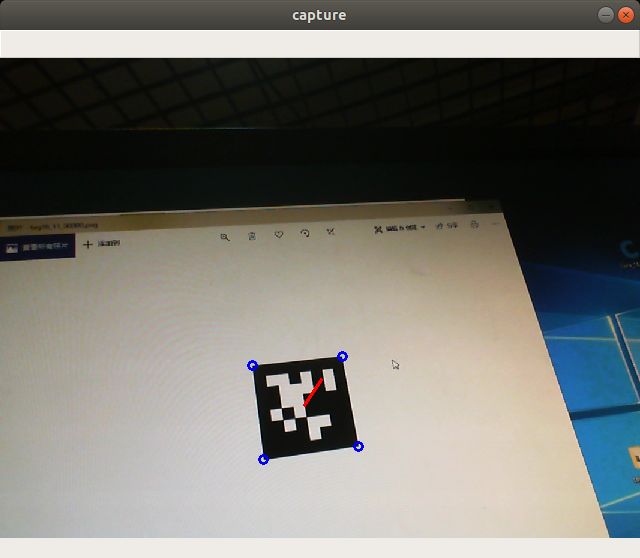
现在仍以apriltag中心为参考坐标系，取apriltag的法向量为$\mathbf{n}=[0,0,-1]$，这也表示了向量的顶端的位置点，将该位置点投影到图像上，得到的点与apriltag的图像中心点的连线即为法线在图像上的投影，用来表示apriltag的方向。

下面是在图像上显示apriltag方向的代码以及测试的结果

      #计算并显示apriltag码的方向
      M,e1,e2=at_detector.detection_pose(tag, cam_params)
      P=M[:3,:4]
      P=np.matmul(K,P)
      x=np.matmul(P,np.array([[0],[0],[-1],[1]]))
      x=x/x[2]
      cv2.line(frame, tuple(tag.center.astype(int)), tuple(x[:2].astype(int)), (0,0,255),2)

下面的图中，将摄像头安装在机器人上，使用的Apriltag码的宽度为0.08m，估计出的距离为0.48 m，和实际量出来的距离基本是一致的。