R语言中的单因素协方差分析

单因素协方差分析（ANCOVA）扩展了单因素方差分析（ANOVA），包含一个或多个定量的协变量。

下面的例子来自于multcomp包中的litter数据集（见Westfall et al.，1999）。怀孕小鼠
被分为四个小组，每个小组接受不同剂量（0、5、50或500）的药物处理。产下幼崽的体重均值为因变量，怀孕时间为协变量

attach(litter)
table(dose)

dose
  0   5  50 500 
 20  19  18  17
aggregate(weight, by = list(dose), FUN = mean)

  Group.1        x
1       0 32.30850
2       5 29.30842
3      50 29.86611
4     500 29.64647
fit <- aov(weight ~ gesttime + dose)
summary(fit)

            Df Sum Sq Mean Sq F value  Pr(>F)   
gesttime     1  134.3  134.30   8.049 0.00597 **
dose         3  137.1   45.71   2.739 0.04988 * 
Residuals   69 1151.3   16.69                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

结论：(a)怀孕时间与幼崽出生体重相关；(b)控制怀孕时间，药物剂量与出生体重相关。控制怀孕时间，确实发现每种药物剂量下幼崽出生体重均值不同

由于使用了协变量，你可能想要获取调整的组均值——即去除协变量效应后的组均值。可使用effects包中的effects()函数来计算调整的均值：

library(effects)
effect("dose", fit)

dose
       0        5       50      500 
32.35367 28.87672 30.56614 29.33460 

par(mfrow=c(2,2))

plot(fit)

评估检验的假设条件

ANCOVA与ANOVA相同，都需要正态性和同方差性假设，ANCOVA还假定回归斜率相同。

验证因变量满足正态分布

library(car)

qqPlot(lm(weight ~gesttime+dose , data = litter), simulate = TRUE, 
    main = "QQ Plot", labels = FALSE)

验证变量的同方差

bartlett.test(weight~dose, data = litter)

data:  weight by dose
Bartlett's K-squared = 9.6497, df = 3, p-value = 0.02179

检验回归斜率的同质性

library(multcomp)
> fit2 <- aov(weight ~ gesttime * dose)
> summary(fit2)
              Df Sum Sq Mean Sq F value  Pr(>F)   
gesttime       1  134.3  134.30   8.289 0.00537 **
dose           3  137.1   45.71   2.821 0.04556 * 
gesttime:dose  3   81.9   27.29   1.684 0.17889   
Residuals     66 1069.4   16.20                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

交互效应不显著，支持了斜率相等的假设。

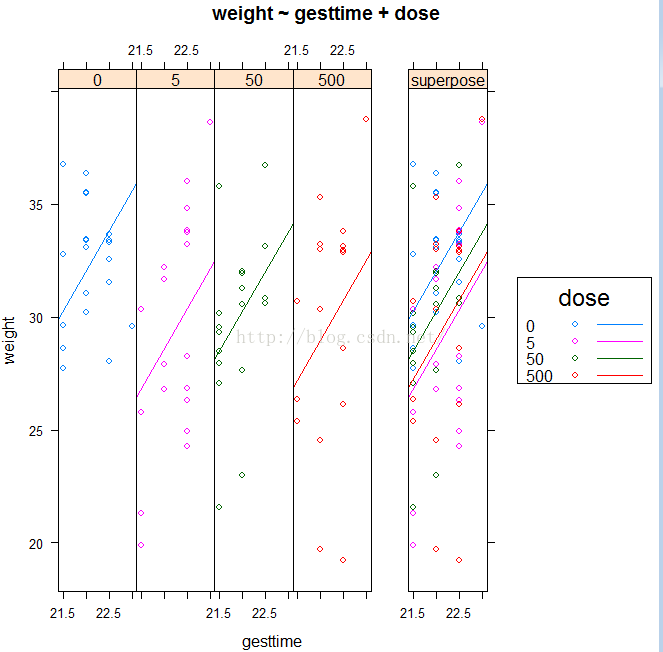
增强处理结果可视化

library(HH)
ancova(weight ~ gesttime + dose, data = litter)

Analysis of Variance Table


Response: weight
          Df  Sum Sq Mean Sq F value   Pr(>F)   
gesttime   1  134.30 134.304  8.0493 0.005971 **
dose       3  137.12  45.708  2.7394 0.049883 * 
Residuals 69 1151.27  16.685                    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1