变分推断（variational inference）

大家对贝叶斯公式应该都很熟悉
$$P(Z|X)=\frac{p(X,Z)}{{\int }_{z}p(X,Z=z)dz}$$

我们称$P(Z|X)$为posterior distribution。posterior distribution的计算通常是非常困难的，为什么呢？
假设$Z$是一个高维的随机变量，如果要求$P(Z=z|X=x)$,我们不可避免的要计算${\int }_{z}p(X=x,Z=z)dz$,由于$Z$是高维随机变量，这个积分是相当难算的。

variational inference就是用来计算posterior distribution的。

core idea

variational inference的核心思想包含两步：

• 假设分布$q(z;\lambda )$ (这个分布是我们搞得定的，搞不定的就没意义了)
• 通过改变分布的参数 $\lambda$ , 使 $q(z;\lambda )$ 靠近 $p(z|x)$

总结称一句话就是，用一个简单的分布 $q(z;\lambda )$ 拟合复杂的分布 $p(z|x)$

这种策略将计算 $p(z|x)$ 的问题转化成优化问题了
$${\lambda }^{\ast }=\arg \underset{\lambda }{\min }divergence(p(z|x),q(z;\lambda ))$$
收敛后，就可以用 $q(z;\lambda )$ 来代替 $p(z|x)$了

公式推倒

对概率求对数

$$\begin{array}{rl}\text{log}P(x)& =\text{log}P(x,z)-\text{log}P(z|x)\\ & =\text{log}\frac{P(x,z)}{Q(z;\lambda )}-\text{log}\frac{P(z|x)}{Q(z;\lambda )}\end{array}$$
等式的两边同时对分布$Q(z)$求期望，可以得到
$$\begin{array}{rl}{\mathbb{E}}_{q(z;\lambda )}\text{log}P(x)& ={\mathbb{E}}_{q(z;\lambda )}\text{log}P(x,z)-{\mathbb{E}}_{q(z;\lambda )}\text{log}P(z|x)\\ \text{log}P(x)& ={\mathbb{E}}_{q(z;\lambda )}\text{log}\frac{p(x,z)}{q(z;\lambda )}-{\mathbb{E}}_{q(z;\lambda )}\text{log}\frac{p(z|x)}{q(z;\lambda )}\\ & =KL(q(z;\lambda )||p(z|x))+{\mathbb{E}}_{q(z;\lambda )}\text{log}\frac{p(x,z)}{q(z;\lambda )}\\ \text{log}P(x)& =KL(q(z;\lambda )||p(z|x))+{\mathbb{E}}_{q(z;\lambda )}\text{log}\frac{p(x,z)}{q(z;\lambda )}\end{array}$$
我们的目标是使 $q(z:\lambda )$ 靠近 $p(z|x)$ ,就是${\min }_{\lambda }KL(q(z;\lambda )||p(z|x))$ ,由于 $KL(q(z;\lambda )||p(z|x))$ 中包含 $p(z|x)$ ，这项非常难求。将$\lambda$看做变量时，$\text{log}P(x)$ 为常量，所以， ${\min }_{\lambda }KL(q(z;\lambda )||p(z|x))$ 等价于 ${\max }_{\lambda }{\mathbb{E}}_{q(z;\lambda )}\text{log}\frac{p(x,z)}{q(z;\lambda )}$。 ${\mathbb{E}}_{q(z;\lambda )}[\text{log}p(x,z)-\text{log}q(z;\lambda )]$ 称为Evidence Lower Bound(ELBO)。

现在，variational inference的目标变成$$\underset{\lambda }{\max }{\mathbb{E}}_{q(z;\lambda )}[\text{log}p(x,z)-\text{log}q(z;\lambda )]$$

为什么称之为ELBO呢？
$p(x)$一般被称之为evidence，又因为 $KL(q||p)>=0$, 所以 $p(x)>=E_{q(z;\lambda )}[\text{log}p(x,z)-\text{log}q(z;\lambda )]$, 这就是为什么被称为ELBO

ELBO

继续看一下ELBO
$$\begin{array}{rl}ELBO(\lambda )& ={\mathbb{E}}_{q(z;\lambda )}[\text{log}p(x,z)-\text{log}q(z;\lambda )]\\ & ={\mathbb{E}}_{q(z;\lambda )}\text{log}p(x,z)-{\mathbb{E}}_{q(z;\lambda )}\text{log}q(z;\lambda )\\ & ={\mathbb{E}}_{q(z;\lambda )}\text{log}p(x,z)+H(q)\end{array}$$
The first term represents an energy. The energy encourages $q$ to focus probability mass where the model puts high probability, $p(\mathbf{x},\mathbf{z})$. The entropy encourages $q$ to spread probability mass to avoid concentrating to one location.

q(Z)

假设$Z$包含K个随机变量( 当然，每个随机变量也有可能为多元随机变量)，我们假设：
$$q(Z;\lambda )=\prod _{k=1}^K{q}_k(Z_k;{\lambda }_k)$$
这个被称为mean field approximation。关于mean field approximation，https://metacademy.org/graphs/concepts/mean_field
ELBO则变成
$$\begin{array}{rl}ELBO(\lambda )& ={\mathbb{E}}_{q(Z;\lambda )}\text{log}p(X,Z)-{\mathbb{E}}_{q(z;\lambda )}\text{log}q(Z;\lambda )\\ & =\int q(Z;\lambda )\text{log}p(X,Z)dZ-\int q(Z;\lambda )\text{log}q(Z;\lambda )dZ\\ & =\int [\prod _{k=1}^K{q}_k(Z_k;{\lambda }_k)]\text{log}p(X,Z)dZ-\int [\prod _{k=1}^K{q}_k(Z_k;{\lambda }_k)]\text{log}q(Z;\lambda )dZ\end{array}$$
第一项为 energy， 第二项为H(q)

energy

符号的含义：

$$Z=\{Z_j,{\overline{Z}}_j\},{\overline{Z}}_j=Z\backslash Z_j$$
$$\lambda =\{{\lambda }_j,{\overline{\lambda }}_j\},{\overline{\lambda }}_j=\lambda \backslash {\lambda }_j$$

先处理第一项：
$$\begin{array}{rl}& \int [\prod _{k=1}^K{q}_k(Z_k;{\lambda }_k)]\text{log}p(X,Z)dZ=\\ & {\int }_{Z_j}{q}_j(Z_j;{\lambda }_j){\int }_{{\overline{Z}}_j}[\prod _{k̸=j}^K{q}_k(Z_k;{\lambda }_k)]\text{log}p(X,Z)d{\overline{Z}}_{j}d{Z}_j=\\ & {\int }_{Z_j}{q}_j(Z_j;{\lambda }_j)[E_{q({\overline{Z}}_j;{\overline{\lambda }}_j)}\text{log}p(X,Z)]d{Z}_j=\\ & {\int }_{Z_j}{q}_j(Z_j;{\lambda }_j)\{\log \exp [E_{q({\overline{Z}}_j;{\overline{\lambda }}_j)}\text{log}p(X,Z)]\}d{Z}_j=\\ & {\int }_{Z_j}{q}_j(Z_j;{\lambda }_j)[\log q_j^{\ast }(Z_j;{\lambda }_j)+\log C]d{Z}_j\end{array}$$
其中$q_j^{\ast }(Z_j;{\lambda }_j)=\frac{1}{C}\exp [E_{q({\overline{Z}}_j;{\overline{\lambda }}_j)}\text{log}p(X,Z)]$ , $C$ 保证 $q_j^{\ast }(Z_j;{\lambda }_j)$ 是一个分布。$C$ 与变分参数 ${\overline{\lambda }}_j$ 有关，与$Z,{\lambda }_j$ 无关！！

H(q)

再处理第二项：
$$\begin{array}{rl}& \int [\prod _{k=1}^K{q}_k(Z_k;{\lambda }_k)]\text{log}q(Z;\lambda )dZ=\\ & \int [\prod _{k=1}^K{q}_k(Z_k;{\lambda }_k)]\sum _{n=1}^K\text{log}q(Z_n;\lambda )dZ=\\ & \sum _j\int [\prod _{k=1}^K{q}_k(Z_k;{\lambda }_k)]\text{log}q(Z_j;{\lambda }_j)dZ=\\ & \sum _j\int [\prod _{k=1}^K{q}_k(Z_k;{\lambda }_k)]\text{log}q(Z_j;{\lambda }_j)dZ=\\ & \sum _j{\int }_{Z_j}{q}_j(Z_j;{\lambda }_j)\text{log}q(Z_j;{\lambda }_j)d{Z}_j\int [\prod _{k̸=j}^K{q}_k(Z_k;{\lambda }_k)]d{\overline{Z}}_j=\\ & \sum _j{\int }_{Z_j}{q}_j(Z_j;{\lambda }_j)\text{log}q(Z_j;{\lambda }_j)d{Z}_j\end{array}$$

再看ELBO

经过上面的处理，ELBO变为
$$\begin{array}{rl}ELBO& ={\int }_{Z_i}{q}_i(Z_i;{\lambda }_j)\text{log}{q}_i^{\ast }(Z_i;{\lambda }_i)d{Z}_i-\sum _j{\int }_{Z_j}{q}_j(Z_j;{\lambda }_j)\text{log}q(Z_j;{\lambda }_j)d{Z}_j+\log C\\ & =\{{\int }_{Z_i}{q}_i(Z_i;{\lambda }_j)\text{log}{q}_i^{\ast }(Z_i;{\lambda }_i)d{Z}_i-{\int }_{Z_i}{q}_i(Z_i;{\lambda }_j)\text{log}q(Z_i;{\lambda }_i)d{Z}_i\}+H(q({\overline{Z}}_i;{\overline{\lambda }}_i))+\log C\\ & \end{array}$$
再看上式 $\{\}$ 中的项：
$${\int }_{Z_i}{q}_i(Z_i;{\lambda }_j)\text{log}{q}_i^{\ast }(Z_i;{\lambda }_i)d{Z}_i-{\int }_{Z_i}{q}_i(Z_i;{\lambda }_j)\text{log}q(Z_i;{\lambda }_i)d{Z}_i=-KL(q_i(Z_i;{\lambda }_j)||q_i^{\ast }(Z_i;{\lambda }_i))$$
所以ELBO又可以写成：
$$ELBO=-KL(q_i(Z_i;{\lambda }_j)||q_i^{\ast }(Z_i;{\lambda }_i))+H(q({\overline{Z}}_i;{\overline{\lambda }}_i))+\log C$$
我们要$maxmizeELBO$，如何更新 $q_i(Z_i;{\lambda }_i)$ 呢？
从
$$ELBO=-KL(q_i(Z_i;{\lambda }_i)||q_i^{\ast }(Z_i;{\lambda }_i))+H(q({\overline{Z}}_i;{\overline{\lambda }}_i))+\log C$$
可以看出，当 $q_i(Z_i;{\lambda }_j)=q_i^{\ast }(Z_i;{\lambda }_i)$ 时， $KL(q_i(Z_i;{\lambda }_j)||q_i^{\ast }(Z_i;{\lambda }_i))=0$ 。 这时，ELBO取最大值。
所以参数更新策略就变成了
$$\begin{array}{rl}& q_1(Z_1;{\lambda }_1)=q_1^{\ast }(Z_1;{\lambda }_1)\\ & q_2(Z_2;{\lambda }_2)=q_2^{\ast }(Z_2;{\lambda }_2)\\ & q_3(Z_3;{\lambda }_3)=q_3^{\ast }(Z_3;{\lambda }_3)\\ & ...\end{array}$$
关于 $q_i^{\ast }(Z_i;{\lambda }_i)$
$$\begin{array}{rl}{q}_i(Z_i;{\lambda }_i)& =q_i^{\ast }(Z_i;{\lambda }_i)\\ q_i(Z_i;{\lambda }_i)& =\frac{1}{C}\exp [E_{q({\overline{Z}}_i;{\overline{\lambda }}_i)}\text{log}p(X,Z)]\\ & =\frac{1}{C}\exp [E_{q({\overline{Z}}_i;{\overline{\lambda }}_i)}\text{log}p(X,Z_i,{\overline{Z}}_i)]\\ & \end{array}$$
$q_i$ 是要更新的节点，$X$ 是观测的数据,由于 Markov Blanket(下面介绍)，更新公式变成：
$$\log (q_i(Z_i;{\lambda }_i))=\int q(mb(Z_i))\log p(Z_i,mb(Z_i),X)dmb(Z_i)$$
由于式子中和 $Z_i$ 无关的项都被积分积掉了，所以写成了 Markov Blanket 这种形式

Markov Blanket

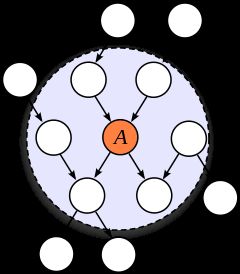
In machine learning, the Markov blanket for a node $A$ in a Bayesian network is the set of nodes $mb(A)$ composed of $A^{\prime }s$ parents, its children, and its children’s other parents. In a Markov random field, the Markov blanket of a node is its set of neighboring nodes.
Every set of nodes in the network is conditionally independent of $A$ when conditioned on the set $mb(A)$, that is, when conditioned on the Markov blanket of the node $A$ . The probability has the Markov property; formally, for distinct nodes $A$ and $B$:
$$Pr(A|mb(A),B)=Pr(A|mb(A))$$
The Markov blanket of a node contains all the variables that shield the node from the rest of the network. This means that the Markov blanket of a node is the only knowledge needed to predict the behavior of that node.

参考资料

https://en.wikipedia.org/wiki/Markov_blanket
http://edwardlib.org/tutorials/inference
http://edwardlib.org/tutorials/variational-inference