#1_《经典控制理论复习》摘录
文章目录
- 1. 基本概念
- 2. 线性系统
- 2.1. 传递函数
- 2.2. 稳定性
- 2.3. 稳态误差
- 2.4. 时域设计指标
- 3. 时域控制方法
- 3.1. PID控制
- 3.2. Root Locus
- 4. 频域控制方法
- 4.1. 基本概念
- 4.2. Bode图法
- 4.3. 奈奎斯特稳定性判据
- 4.4. 稳定裕度
- 4.5. 根据Bode图设计系统
- 4.6. 闭环系统频域指标
- 5. 控制器的设计过程
- 参考文献
本文主要目的是复习经典控制理论的相关知识,主要参考知乎专栏 1。
作者声明不要私自转载,我这篇主要是摘录了部分,结合自己的理解进行了记录,并补充了一些我关心的内容。如果作者觉得不妥,请联系我,马上删除。
学控制的人,一定要对信号处理与系统有了解,信号处理,系统理论和动力学与自动控制理论都有紧密的联系。控制理论的研究如今偏向于数学化,有些著作初看已经与实际工程不容易联系在一起了,而经典方法在应用中非常实用,夯实基础是必要的。
推荐的经典教程有:
自动控制原理(胡寿松)、Signals & Systems(Alan V. Oppenheim)、Feedback Control of Dynamic Systems(Gene F. Franklin)。
1. 基本概念
控制系统的结构
闭环控制系统的目标是,使系统测量值等于系统的输入值,结构如下:
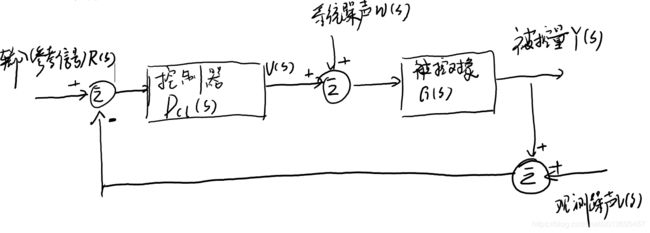
控制问题的三大类
①调节/镇定问题 Regulation
控制系统输出并保持到某一个预定的工作点(set point)。该问题中,reference input R ( s ) R(s) R(s)应当是一个已知的常值。Regulation的目标就是设计一个控制器(controller)或者叫补偿器(compensator),我们也常称调节问题的控制器为调节器(regulator),使得plant或者process能够维持在设定的set point(set point由reference input确定),并且在受到外来干扰时,控制器需要做出动作,自动调节系统状态以再次到达原来设定的set point。
我们希望调节的速度越快越好,调节的准确度越高越好,并且控制器输出信号功率越小越好(节能),这些指标反映了控制品质。
②跟踪问题 Tracking
实现控制系统的输出实时地跟踪参考输入信号,reference input是变化的。Tracking问题中,输入是未知的,可以视为随机的,我们往往知道这个随机信号的特征,例如函数形式等。实现Tracking的系统结构和Regulation相差是不大的。
③程序控制 Program-based control
这一类问题往往采用开环控制。程序控制中的参考信号一般都是预定规律随时间变化的函数,被控对象只需要复现此信号即可。举例:交通信号灯、自动门。在控制精度要求不高或者干扰很小、干扰可知的场合中,多数的程序控制问题会采用开环控制,这样系统的响应速度能大大加快。工业制造上的机械手,数控机床和PLC等都是程序控制的案例,它们根据事先编好的程序进行运行,而不需要输出信息来干预输入。
控制理论主要还是讨论①和②的情形。
控制系统的数学模型
系统可以用微分方程描述,在控制理论中多见的是常微分方程(Ordinary Differential Equation),ODE描述了系统的运动规律。ODE分为线性(Linear)和非线性(Nonlinear)的。在经典控制的范畴中,我们关注点主要在线性常系数ODE,也会涉及到非常系数的ODE。前者描述的系统我们称之为线性时不变系统,或者常称为线性定常系统(Linear Time-Invariant System,LTI System)。经典控制理论主要研究LTI系统,但是实际问题往往不符合LTI,因此常在工作点附近做线性化处理。
我的天,这博客太有启发了,之前相当于根本不懂啊,我只记录要点吧,博客还得反复看!
①经典控制理论主要关注SISO的LTI系统,我们需要从这个最简单情形出发思考控制问题;
②控制与数学是紧密结合的,SISO LTI系统和线性常系数ODE求解关系非常紧密,必须要认真对待数学(微分方程求解、矩阵);
③如果系统是LTI的,那么系统响应完全可通过微分方程理解:
线性常系数ODE全解 = 齐次方程非零初始条件解 + 非齐次方程零初始条件解 →
LTI系统Complete response = Zero State Response+ Zero Input Response
④如果系统是非线性的,我们需要采用小扰动Taylor展开的方法,将其化为线性问题,这要求系统的解轨迹(trajectory)不远离展开点附近,那么:
1.原非线性方程解空间中这么多点,究竟要在哪个点进行线性化?
对于Regulation问题,我们需要在set point附近线性化,这个稳态时的点,也叫做系统的稳定平衡点(stable equilibrium);对于Tracking问题,则首先改写为误差的微分方程,然后在0点展开(我们希望误差为0)。
2.线性化后得到的线性方程,怎么保证解就能在原来展开点的附近呢(这样线性化处理才有意义)?
对于一个非线性微分方程,可能本身就存在自身稳定平衡点(在该点附近,系统会自动落向该点,该区域叫做吸引域),也可能不存在,但是我们却希望在指定点附近线性化,那么就需要通过设计控制器改变系统的微分方程(系统结构),使其在我们期望的点上出现稳定平衡点。由于要线性化,那么要求系统状态要被约束在吸引域,一旦在干扰等原因下跑出去,就会发散掉,那么我们就希望加入控制器后,系统的吸引域大一些(更鲁棒)!当然,系统可能无论如何也不能把稳定平衡点调整到期望的点上,这就涉及到可控性问题。
经典控制理论的发展历史
自1783年James Watt改良可实用的蒸汽机后,John Rennie采用了离心调速器(Centrifugal Governor)自动控制了蒸汽机的轻质节流阀(throttle valve)。后续人们又开发出了类似的离心调速器,但是节流阀的控制却出现了不稳定现象,这一直困扰着工程师。直到大名鼎鼎的 J.C. Maxwell通过建立微分方程,发现只有系统微分方程的各根具有负实部才能保证系统的稳定性。
1877年数学家Edward John Routh和后来1895年数学家Adolf Hurwitz都贡献了通过特征方程系数判断稳定性的方法,一般可以把他们的成果合称为 Routh-Hurwitz Criteria。
1922年俄国人 Nicolas Minorsky发表论文阐述PID控制律。
1927年Bell Labs的Harold Black发明了负反馈放大器(Negative Feedback Amplifer)。
1932年物理学博士Harry Nyquist发表频域稳定性判据:Nyquist Criterion。
1938年物理学博士Hendrik Bode提出Bode plot,1940发表阐述Bode定理,相位裕度(Phase Margin)和幅值裕度(Gain Margin)用于控制系统分析与设计。
1942年Ziegler和Nichols发表Ziegler-Nichols Method,用于整定PID控制器参数。Nichols 后提出了Nichols Chart,成为控制图解设计的重要工具。
1940年代末期,Evans提出Root Locus理论。
2. 线性系统
2.1. 传递函数
emmm,好懵逼,关键是数学上理解不到位吧,,,不过还是有所收获,简要总结一下,日后回过头来深入研究。
对于一个LTI系统,在零初态情况下:
①任意输入的相应都能分解成卷积的形式:


其中, u ( t ) u(t) u(t)是输入函数, h ( t ) h(t) h(t)是系统单位脉冲响应(得求解微分方程得到输出的函数,然后根据单位脉冲响应的筛选性质即可得到,参考这里), y ( t ) y(t) y(t)是系统输出。
②为了简化计算,从时域变换到s域:
Laplace变换:函数 y ( t ) y(t) y(t)的Laplace变换为:
Y ( s ) = ∫ 0 ∞ y ( t ) e − s t d t Y(s)=\int_{0}^{\infty}{y(t)e^{-st}dt} Y(s)=∫0∞y(t)e−stdt
对上述卷积进行Laplace变换,有:

可见在s域形式非常简单,称其中的 H ( s ) H(s) H(s)为传递函数,也即单位脉冲响应的Laplace变换,直接由系统结构决定,注意前提是零初始条件。
传递函数既然要满足零初始条件,那利用传递函数显然只能得到零状态响应,也就是只关心输入对系统输出造成的影响。因此必须讨论零初态假设的合理性。
对于一个LTI系统而言,初始状态并不会影响其本身具有的某些性质,比如稳定性,我们认为传递函数足以能够让我们能够研究一个LTI系统中我们所关心的性质。从微分方程解的角度来讲,零状态响应的解结构与全响应解结构是一样的,都是通解+特解的组合,只是零状态响应的系数发生了变化。
③零极点
由 H ( s ) = Y ( s ) U ( s ) H(s)=\frac{Y(s)}{U(s)} H(s)=U(s)Y(s)
使得 分 子 = 0 分子=0 分子=0的点为零点,使得 分 母 = 0 分母=0 分母=0的点为极点。而极点是微分方程的特征根,因此极点数值和数量决定了ODE解的模态结构,更进一步地,模态的结构最后影响了系统响应的动态和稳态。
具体的:

零点会对每个模态的大小产生影响,与极点接近时会引起零极点相消,从而减小该极点对应模态的影响。
④实际系统的传递函数,分子的阶次不应大于分母的阶次,并且所有物理系统系统都是满足分子阶次小于等于分母的。如果分子的阶次大于分母,那么任何一个常值信号,或者阶跃信号都会使系统响应无限增长,这样的系统现实中是不存在的。
2.2. 稳定性
设计控制器首要目标就是让系统稳定,然后在此基础上改善性能。
这一小节梳理了稳定性的各种概念,简述如下:
①一些概念:
平衡状态:系统各个状态的变化率为0时的系统状态。对于LTI系统而言,只有一个平衡态或者无穷多个平衡态或者没有平衡态三种可能。而非线性系统则可能有多个平衡态。
平衡态稳定性:系统在平衡状态下如果受到一定程度的扰动而偏离了原来的平衡状态,当扰动消失后仍然能恢复到原有平衡状态的能力。
运动稳定性:线性系统由线性微分方程所描述,其稳定性也就是线性微分方程解的稳定性,即给定初值,在无输入的情况下,当时间趋于无穷时解是否渐进收敛于某个值。对于LTI系统来讲,就是考察其齐次微分方程的通解的稳定性,即零输入响应的稳定性。
BIBO稳定性:BIBO稳定性被称为外部稳定性,因其由输入与输出所定义,这正是传递函数的定义方式,输出对应系统零状态响应。LTI系统的内部稳定性,即平衡状态稳定性由其特征值来决定。这两种稳定性在没有零极点相消时,即零状态响应完整地表现了原有系统的模态时,是等价的。如果内部稳定显然可以推得外部稳定。
前馈与反馈:feedforward vs. feedback = 开环 vs. 闭环。
②如果LTI系统只有唯一个平衡态,且证明其特征值实部均为负,那么其所有解一定具有运动稳定性,可称系统也具有运动稳定性,而该平衡态(零)是稳定性的,系统也由此认为是平衡态稳定的。最后可以得出,满足这样条件的LTI系统稳定。
在非线性系统里系统的初值对最后解的去向和结构是存在重大影响的,这一点也线性系统有很大的差别。在线性系统中解的稳定性是由系统的结构和参数确定的,而与初值无关(但是特殊初值会改变解的组成)。
③经典控制理论中的稳定性主要都是指BIBO稳定性,这是由传递函数自身反映系统的能力决定的。用传递函数来判断平衡态稳定性,隐含的条件就是系统没有发生零极点相消,此时内部稳定等于外部稳定。
如果设计补偿器与开环系统串联能够消除其传递函数中的不稳定极点,则系统是BIBO稳定的。但是注意,这里的“消除”只是因为在零初始条件下,系统响应中的不稳定模态前的系数刚好为0。因此开环不稳定系统只能采用闭环控制策略。
④判断微分方程稳定性(内稳定)的方法:
Routh Array,Hurwitz criterion,Root Locus等工具。
2.3. 稳态误差
对于如下结构的系统,定义误差为输入和输出之差,那么误差为:
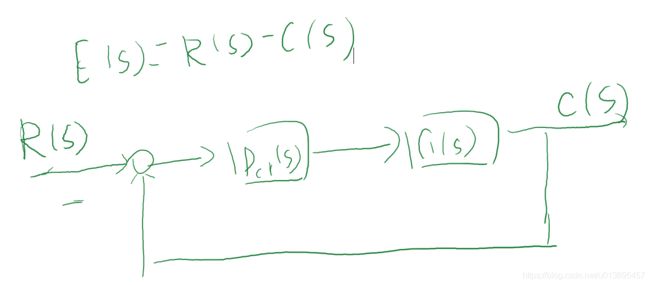

首先判断系统稳定性!如果系统是稳定的,稳态误差可以直接使用终值定理计算:
e s s = lim s → 0 s E ( s ) e_{ss}=\lim_{s \to 0} sE(s) ess=lims→0sE(s)
假设输入是多项式形式的,我们可以只考虑最高次数的项分析稳态误差,设其传递函数为: R ( s ) = 1 s k + 1 R(s)=\frac{1}{s^{k+1}} R(s)=sk+11, k k k表示输入阶次,例如对于阶跃信号, k = 0 k=0 k=0,斜坡信号 k = 1 k=1 k=1。我们假设系统开环传递函数有 n n n个积分环节,该系统为Type n,即: G D c l = G D c l ′ ( s ) s n GD_{cl}=\frac{GD_{cl'}(s)}{s^n} GDcl=snGDcl′(s),那么稳态误差为:

结论为:
n − k > 0 n-k>0 n−k>0,则没有稳态误差;
n − k = 0 n-k=0 n−k=0,则稳态误差为常数;
n − k < 0 n-k<0 n−k<0,则系统发散,无法跟踪这么高阶的系统。
此外,还可以讨论噪声的阶数和系统稳定性的关系,对于输入噪声,与上述对输入的讨论完全相同,对于系统噪声和观测噪声,也可以进行讨论。
该系统的Type反应了系统鲁棒性的一个方面。
2.4. 时域设计指标
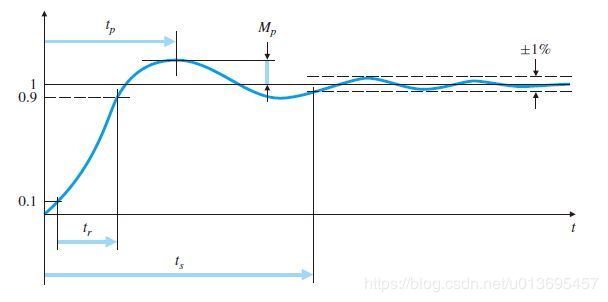
其中: t r t_r tr为上升时间, t p t_p tp为调节时间, M p M_p Mp为超调量, t s t_s ts为调节时间。
对于一阶系统,因为没有超调,只需要考虑上升时间;对于二阶及以上系统则需要综合考虑。对于没有零点的二阶系统( ω n \omega_n ωn为无阻尼振荡角频率或者自然角频率, ζ \zeta ζ为阻尼比,两者决定了系统的响应):

以上二阶系统的几个指标都有公式或者近似公式,无需记忆,需要时可以查阅。但是我们从中可以得到一些结论,这些结论可以扩展到更高阶的系统:
①对于上升时间:如果想要一个二阶系统的响应速度变快,增大系统自然频率,减小系统阻尼比是两种手段。
②对于超调量:阻尼比越大,超调量越小。
③对于调节时间:阻尼比与自然角频率乘积越大,调节时间越小。
3. 时域控制方法
3.1. PID控制
PID既可以适用于有模型的系统,也可以适用于无模型的系统,其原理也非常简单。
①比例控制:
比例控制P control能够提高系统的响应速度和稳态精度,抑制扰动对系统稳态的影响。但过大的比例控制容易导致系统超调和振荡,并且有可能使得系统变得不稳定。 纯比例控制并不能消除稳态误差,存在静差。
纯比例控制会产生稳态误差的原因是其无法改变系统的型号。如果参考信号的阶次大于等于系统自身的阶次,那么无论如何选取纯比例控制的K值都无法使得稳态误差消除。
②积分控制:
参考稳态误差公式:

引入积分环节可以增大n的值,改变到一定程度,即可使系统从发散或者恒值的稳态误差改变为0稳态误差。因此积分环节的主要作用就是消除稳态误差。
对于常值信号(阶跃),如果系统传递函数 G ( s ) G(s) G(s)是Type 0的,那么引入如下形式的积分环节可以有效消除稳态误差:

以上定义的积分控制消除稳态误差的作用对于高阶的参考信号和扰动是无效的。积分控制并不一定是必须的,应当视系统的型号、输入和干扰类型决定。
③微分控制:
提供一定的阻尼,抑制系统的超调和震荡。微分控制D control的主要作用就是减少超调量,加速瞬态过程和提高系统的稳定性。
微分控制一般会和P control一起使用,组成PD控制。D控制单独使用并不能起到很好的效果,因为当误差保持为常数时,显然控制量就会变为0。
注意,微分器会对高频噪音有放大的效果。
④联合使用:
单独使用I和D都存在弊端,它们往往会和P一起使用,以加快系统响应速度和减小稳态误差的作用。PID改变系统动态以及稳态的直接原因就是因为控制器的引入改变了闭环系统的特征方程,从而对系统的模态和解产生了影响。PID控制的完整形式为:
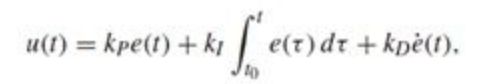
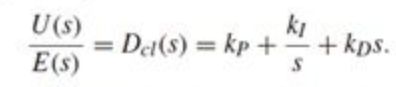
对于简单低阶系统,PID参数可以通过稳定性条件得到大致范围,然后根据需要的动态手动进行调整得到。对于高阶的系统,如果模型已知,我们可以通过Routh Array或者Hurwitz Criterion来判断参数的范围。对于无模型的系统,可以根据根据系统曲线进行PID tuning:方法有Ziegler-Nichols Tuning Method,临界比例度法,衰减曲线法等等。
PID的调节技巧可以参考:《自动调节系统解析与PID整定》一书。另外可以再研究下ADRC相关的知识。
3.2. Root Locus
一个LTI开环系统的闭环特征方程的所有根在s平面上(复平面)随着某一开环系统参数从零到无穷变化产生的轨迹称为该系统的根轨迹(Root Locus)。特征根影响了系统的闭环性能,所以根轨迹方法是用于闭环系统的分析与设计。虽然Bode早就提出了频域设计方法,Nyquist提出了频域稳定性判据,根轨迹可以更方便地研究参数变化时,系统性能的变化,尤其是高阶系统的性能。
对于一个闭环系统:
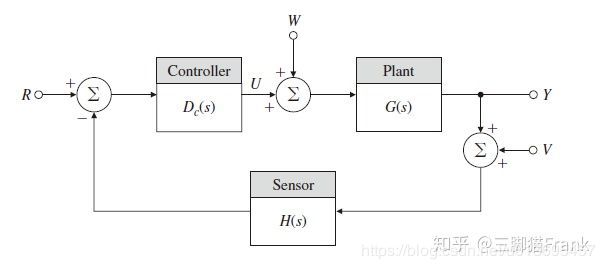
闭环传递函数为:

D c ( s ) G ( s ) H ( s ) D_c(s)G(s)H(s) Dc(s)G(s)H(s)一般是一个分式,比如是 K b ( s ) a ( s ) K\frac{b(s)}{a(s)} Ka(s)b(s),那么带入闭环传函可以得到特征方程:
a ( s ) + K b ( s ) = 0 a(s)+Kb(s)=0 a(s)+Kb(s)=0,定义 L ( s ) = b ( s ) a ( s ) L(s)=\frac{b(s)}{a(s)} L(s)=a(s)b(s),考虑 K K K为我们研究的参数,那么可以写出如下几种root-locus形式:
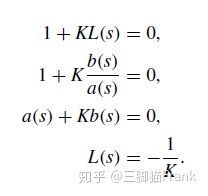
我们研究的就是如何画出以上方程解随参数 K K K变化的轨迹。
参数从0变化到无穷的根轨迹我们一般叫做Positive root locus或者180°根轨迹;对应的,参数从负无穷变化到0的根轨迹叫做Negative root locus或者0°根轨迹。
高阶方程求公式解很复杂,因此根轨迹法提供了根据开环传递函数 K b ( s ) a ( s ) K\frac{b(s)}{a(s)} Ka(s)b(s)的零极点大致绘制根轨迹(闭环传递函数极点轨迹)的方法。我们现在用matlab就好。
画好根轨迹后,在轨迹上取点,对应的K也很好计算,只需把这个点带入 K = − 1 L ( s ) = − 1 ∣ L ( s ) ∣ K = -\frac{1}{L(s)}=-\frac{1}{|L(s)|} K=−L(s)1=−∣L(s)∣1,带入计算就好。
很多东西的记忆,只有基于真正理解才能牢固记住。感谢作者,写得很好,学校的控制课很多东西都没讲透。
结合时域指标,我们可以从根轨迹上找到合适的点,从而完成控制系统设计。例如对于无零点二阶系统,我们要求系统满足上升时间(虽然上升时间和阻尼比也有关系,但是由于与超调冲突,所有这里主要用自然频率控制)、调节时间、超调的要求:


只要满足极点在上图给出的曲线左侧即可。为了能达到要求,我们需要添加控制器,使得根轨迹能够延伸到预定区域。
实用的控制器主要有两类:
①超前补偿器,近似于PD
其主要作用就是加快系统响应速度并且减小瞬态的超调量。之所有这样设计是因为微分环节物理上是无法实现的。超前补偿器形式为(z
大的p值可以更好地逼近PD控制器的效果,而小的p值对应根轨迹的改变并不是十分突出。加入后,实现同样的自然角频率,可以得到更大的阻尼比。
一般地,z值会放在闭环系统的自然频率附近,p值一般与z值的位置5倍到20倍的距离。但是实际中p的选择面临矛盾,为了更接近PD我们需要更大的p值,而为了减小纯PD控制引入的噪音,我们又希望减小p值。我们需要选择合适的p值平衡利弊。
选择完了z与p的值后,我们只需要在根轨迹图中选择合适的增益K满足设计指标,就可以确定我们需要的超前补偿器的传递函数了。
使用一个或者多个超前补偿器得到想要的系统动态性能,但是我们此时可能发现开环系统低频时候的增益可能非常低,导致稳态误差放大,因此需要引入滞后补偿器。
②滞后补偿器,近似于PI
主要作用是提高系统低频时的增益,从而减小系统的稳态误差。

z / p z/p z/p的比值大一些可以提高低频增益的倍数,注意这里没有K,而且与超前补偿相比z和p的关系是相反的。
选择完了z与p的比值,我们还需要lag compensator的零极点不能够影响到系统的主极点,否则加入的补偿器就会严重干扰之前设计好的动态指标。这样我们自然容易把z与p的值选择小一些以远离原来设计好的零极点,但是这样做又会产生一个问题,就是极点过于靠近虚轴会导致该极点对应的闭环系统模态衰减过于缓慢,因此太小的p值会影响调节时间。于是z与p的位置选择也存在compromise。
最后z与p的选择可以通过不断trial and error来找到。最后画出根轨迹图,检验最后的设计指标是否都得到了满足,包括动态指标(上升时间,超调量,峰值时间)和稳态指标(调节时间,稳态误差等)。
根轨迹设计法在控制上已经属于比较古老的设计方法了。现代控制理论引入了矩阵和状态空间方法来研究最优控制。我们可以使用根轨迹来得到一个满足设计要求的控制器(补偿器),但是我们除了这些时域指标,还存在另外的指标来评判控制器设计的好坏,比如control effort的大小,即达到同样控制效果的所花费的控制量,是否达到了最优。传统的根轨迹方法并不能解决最优化的问题,这些问题就要等到之后现代控制理论以及最优控制部分去解答了。
4. 频域控制方法
虽然现代控制技术多已经转向以状态空间分析法为主的时域分析方法,但是频域分析方法在实际工程中依旧能够提供丰富的信息。
频域分析与设计法是经典控制理论的核心内容。频域法中用到的Bode plot,Nyquist plot等是工程中控制设计与分析有力的工具。
在频域分析与设计中,我们有频域中的系统性能指标,以及设计相应指标的设计方法。在频域中,利用Bode plot和Nyquist plot等图解方法可以高效地完成SISO系统的设计工作。
4.1. 基本概念
①频率响应:通常是指LTI系统对正弦类信号的响应。如果LTI系统是稳定的,当瞬态消失后,最后响应只留下的稳态信号依旧是正弦类信号,只是幅值和相位发生了改变,频率不变。这一点在非线性系统或者时变系统中不成立,输出的信号最后可能含有除了输入信号频率之外的频率。
经过分析可以得到,输入正弦信号(幅值应该是1吧?)后,系统的响应由传递函数决定,且可以分解为幅频响应和相频响应:
![]()
称 A ( ω ) A(\omega) A(ω)为幅频特性, ϕ ( ω ) \phi(\omega) ϕ(ω)为相频特性,联合起来叫做频率特性。
4.2. Bode图法
知道结论即可,具体绘制现在可以依靠matlab。
①定义
Bode图中很多定义是有来源的,比如分贝的定义:
Bode图中的分贝
Power dB的标准定义式是功率之比的以10为底的对数的十倍:
又因为功率与电压的平方成正比,所以功率增益power gain也可以写作:
这就是Bode图中分贝如此定义的原因。
Bode Plot 由对数幅频曲线和对数相频曲线组成。在Bode Plot中频率特性 ∣ G ( j w ) ∣ |G(jw)| ∣G(jw)∣可以根据对数的性质分解成独立乘积项的对数之和差。一般纵轴上的幅值会以分贝(dB)为单位;Bode的横轴采用的对数分度,当频率增大10倍时,坐标轴上距离变化为一个单位长度。
总结一下:幅频曲线的横坐标为对数频率,纵坐标为分别;相频曲线横坐标为对数频率,纵坐标就是相角(不取对数)。
②基本思路
频域设计法和根轨迹设计法中设计闭环控制系统的思路是一样的,即通过系统开环传递函数(GH)来设计对应的闭环系统指标,达到设计要求。所以应该明确一般设计控制器时,我们都会根据开环传递函数(Open loop transfer function,OLTF)来画开环Bode plot。
设计开环Bode plot的意义在于我们可以不断调整开环传递函数(OLTF),其中包含了我们想要设计的控制器或者补偿器部分,来实现达到闭环设计指标[相位裕度(phase margin,PM),幅值裕度(gain margin,GM),穿越频率(crossover frequency)等开环频域指标]的目的。
我们也可以画闭环Bode plot。闭环Bode plot是闭环系统在频域中幅值与相位的图示。这与时域中闭环系统的响应曲线表示系统性能的意义是一致的,即闭环Bode plot中我们也可以定义闭环频域指标,我们将闭环频域指标与闭环时域指标进行对应。所以时域指标就可以转化为频域指标,通过频域设计的方法实现。
因此,总的流程为:设计controller(or compensator) → \to →画出开环传递函数DGH的Bode plot → \to →根据开环频域指标调整设计 → \to → 画出闭环传递函数的Bode plot → 检验各闭环指标
③闭环系统频率指标:带宽
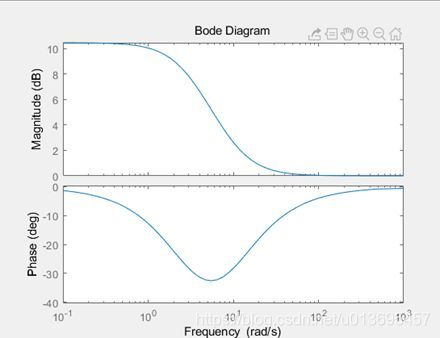
直流增益衰减-3dB的时候的频率即带宽,也就是此时增益衰减到了原来的70.7%,而功率由于是平方关系,衰减一半。在带宽频率之内我们认为系统的输出还是能够很好的跟踪正弦输入的,超出带宽之外我们发现幅值随着频率会骤然下降。低通滤波器的截止频率(Cutoff frequency)和这里的带宽定义式一致的。
对于二阶无零点系统,带宽指标类似于上升时间和峰值时间,阻尼比0.7左右时,带宽和自然频率基本相等,从而可以用带宽来替代自然频率估计系统性能,在其他阻尼比时也可以近似这样处理。
带宽只适用于分子阶次小于分母阶次的系统,此时系统相当于低通滤波器,因此可以抑制高频噪声,而保留住低频信号。对于无零点二阶系统,不同的参数取值可以绘制如下一组曲线。
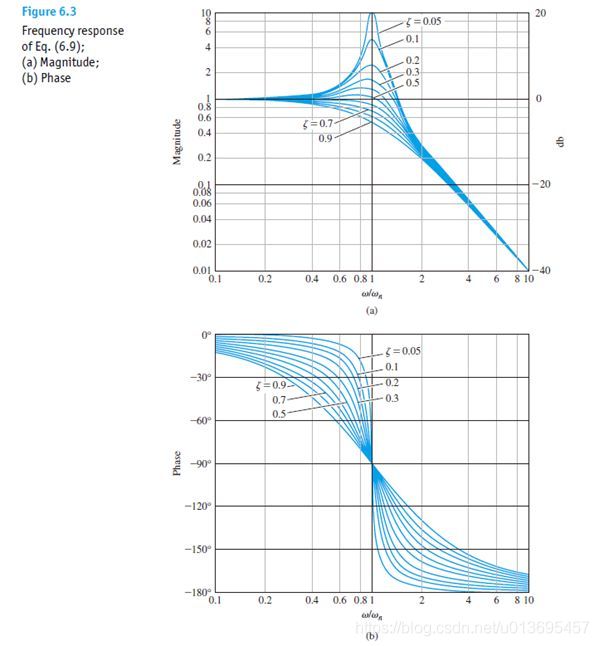
带宽越大,这个系统响应速度就越快,这个结论是显然的,因为带宽越大,系统能通过更高频的信号成分,因此响应速度变快。
对于分子分母同阶数的系统,带宽定义就不合适了,此时系统是“高通低阻”的,类似于高通滤波器:
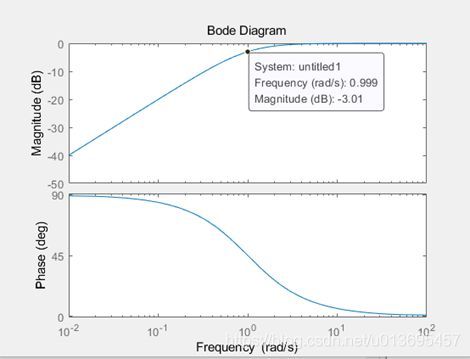
④频率特性与稳态误差
显然,对于实际系统我们发现随着频率的增加,输出信号的幅值会越来越小,这意味着正弦类信号的稳态误差会随着频率的增大而逐渐增大,误差的最大值应该会逼近原输入信号的幅值(因为幅频随着频率会趋于无穷小)。
大的直流增益可以减小闭环系统的稳态误差。如果某个系统其开环传递函数中有n个积分器,对应的频率特性在低频段我们可以得到一个近似的结果:
![]()
也就是:
![]()
其中, K ( j ω ) K(j\omega) K(jω)表示去除积分器后的传递函数, K 0 K_0 K0表示去除积分环节后的直流增益,每增加一个开环积分环节,低频部分斜率增加-20dB。
⑤波特图的绘制
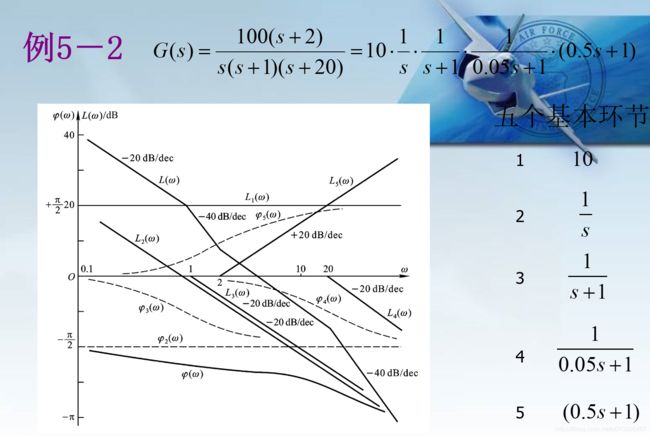
Bode Plot一大优点就是把整个频率特性的作图分解为传递函数的不同零极点和增益的幅频和相频曲线的简单叠加。通过研究每个零极点和增益的幅相曲线,就可以理解每个环节在整体系统中作用。最后通过叠加把所有环节的曲线相加,就可以得到最后的Bode Plot。
具体绘制方法为:
首先,将 G ( s ) G(s) G(s)中的s替换为 j ω j\omega jω,并改写为如下形式:
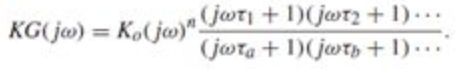
注意n一般是负数,比如一阶系统n=-1。我们需要分别画出幅频特性和相频特性,因此需要从上式得到幅频函数和相频函数,幅频取模长即可,相频则根据复变函数原理得到(各个环节相角相加减)。然后取对数,并乘20得到。然后分别分析各个典型环节,比例、积分微分、惯性和一阶微分、二阶微分和震荡环节,画出各个环节的曲线,然后相加即可。
纯比例环节 G ( j ω ) = K G(j\omega)=K G(jω)=K(下图中 K = 5 K=5 K=5):
纯微分环节 G ( j ω ) = j ω G(j\omega)=j\omega G(jω)=jω:
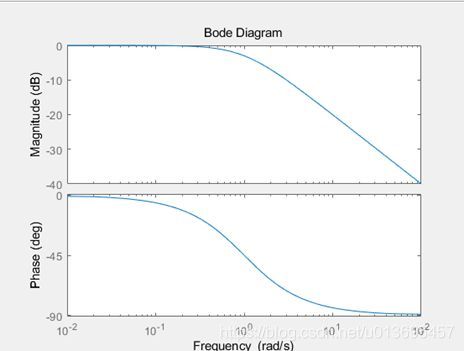
纯积分环节 G ( j ω ) = 1 j ω G(j\omega)=\frac{1}{j\omega} G(jω)=jω1:
前面介绍的超前和滞后环节在频域上体现为对相频曲线的超前和滞后:
滞后环节取K=1, z=10, p=3时效果为:
超前环节取z=2, p=1000时效果为:
一阶微分环节 G ( j ω ) = T j ω + 1 G(j\omega)=Tj\omega+1 G(jω)=Tjω+1,转折频率为 ω = 1 T \omega=\frac{1}{T} ω=T1:
惯性环节 G ( j ω ) = 1 T s + 1 G(j\omega)=\frac{1}{Ts+1} G(jω)=Ts+11:
此外还有二阶环节。唉算了,用matlab画图算了。
要想明白其中的原理才能牢牢记住。
我们以如下系统为例:

从根轨迹分析稳定性:我们从根轨迹出发进行分析,得知只有K<2时系统才是稳定的,那么根据系统闭环特征方程:
1 + K G = 0 1+KG=0 1+KG=0,由于K是实数,因而有:
G ( j ω ) = − 1 K G(j\omega)=-\frac{1}{K} G(jω)=−K1,那么有:
∣ G ( j ω ) ∣ = 1 K , ∠ G ( j ω ) = − 180 ° |G(j\omega)|=\frac{1}{K},\angle G(j\omega)=-180° ∣G(jω)∣=K1,∠G(jω)=−180°
那么我们的思路就是分析频率曲线上,相移为 − 180 ° -180° −180°的那个点,这个点一定位于根轨迹上,满足 ∣ G ( j ω ) ∣ = 1 K |G(j\omega)|=\frac{1}{K} ∣G(jω)∣=K1,我们记这时候的频率为 ω 0 \omega_0 ω0,此时如果系统稳定,那么必有 ∣ K G ( j ω 0 ) ∣ < 1 |KG(j\omega_0)|<1 ∣KG(jω0)∣<1[这说明 K < 1 ∣ G ( j ω ) ∣ K<\frac{1}{|G(j\omega)|} K<∣G(jω)∣1],那么对应到分贝也就是0db。
总结一下,我们只需要在相频曲线上找到 − 180 ° -180° −180°的位置,然后在幅频曲线上找到对应的点,小于0db就是稳定的。
注意,Bode图稳定性判断只适合特定的系统,有些系统却是小增益不稳定,大增益稳定的,更有系统的幅频曲线会穿越1或者0dB数次,从而这样的从Bode Plot去判断稳定性就变得不确定了。但是不管怎样,我们总是可以画根轨迹去判断KG的稳定性的。 由于Bode Plot对某些系统的稳定性判断并不是那么明朗,可以采用Nyquist稳定性判断方法。
4.3. 奈奎斯特稳定性判据
只需要了解原理,用matlab会方便很多。
这是根据幅相曲线进行分析的。概略绘制幅相曲线的要点为:

开环幅相曲线的绘制方法:



非最小相位环节为类似于 1 T s − 1 \frac{1}{Ts-1} Ts−11的环节。这一点还需要仔细研究。
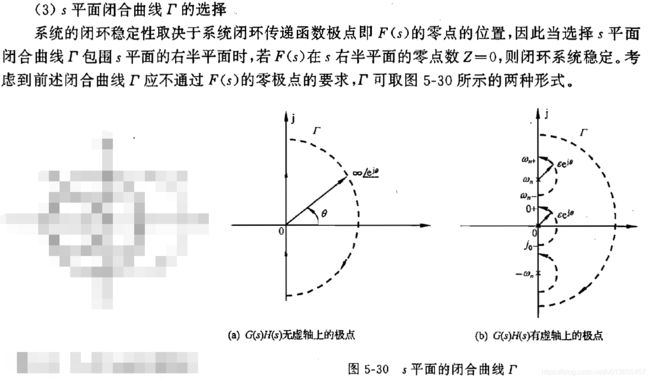
绘制奈奎斯特曲线:
主要还是上面介绍的绘制幅相曲线绘制方法,但是对于积分环节需要补充:

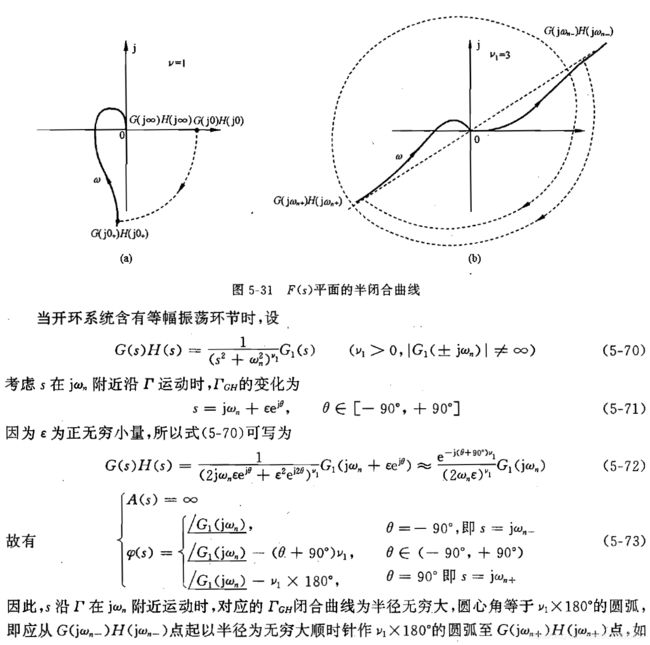
![]()
稳定性判据(注意补作的圆弧):

如果没有穿透,则只计算半次穿越。因此,稳定性条件为:

此外,还可以在对数幅频/相频曲线上应用奈奎斯特判据:
考虑复平面 ( − 1 , j 0 ) (-1, j0) (−1,j0)的点,映射到对数曲线上,相当于 A ( ω c ) = 1 , L ( ω c ) = 0 A(\omega_c)=1,L(\omega_c)=0 A(ωc)=1,L(ωc)=0,称 ω c \omega_c ωc为截止频率。复平面负实轴所有点满足 φ ( ω ) = ( 2 k + 1 ) π \varphi(\omega)=(2k+1)\pi φ(ω)=(2k+1)π,因此我的得到结论:
在 ω c \omega_c ωc之前的频率,且满足 φ ( ω ) = ( 2 k + 1 ) π \varphi(\omega)=(2k+1)\pi φ(ω)=(2k+1)π的位置即对应着复平面的 ( − ∞ , − 1 ) (-\infty, -1) (−∞,−1)的范围的实轴,我们分析在相频 ( l o g 0 , l o g ω c ) (log0, log\omega_c) (log0,logωc)的区间[这是对一般系统,有时候由于幅频曲线不是单调下降的,因此要分析所有的 A ( ω ) > 0 A(\omega)>0 A(ω)>0区间],相频曲线对 φ ( ω ) = ( 2 k + 1 ) π \varphi(\omega)=(2k+1)\pi φ(ω)=(2k+1)π的穿越情况,就等价于分析幅相曲线,但是穿越的方向相反:
从上向下为负穿越 N − N^- N−,从下向上为正穿越 N + N^+ N+。
注意,对于有积分的系统,需要在相频曲线开始的地方,从横轴向下画 v ∗ π / 2 v*\pi/2 v∗π/2的竖线,这等价于幅相曲线中补画的圆弧。
4.4. 稳定裕度
指幅值裕度和相位裕度,衡量距离系统不稳定的某个量变化的宽裕程度。这里只讨论最小相位系统(minimum phase system)。
①定义
在Bode图中的定义很明确:
幅值裕度(Gain Margin,GM),对数相频曲线-180°位置对应的对数幅频曲线上点的值取反(回顾一下只有小于0dB才是稳定的);
相位裕度(Phase Margin,PM),对数幅频曲线0dB的位置对应的对数相频曲线上的点的相位超前-180°的角度(稳定系统该值总是正的)。
在奈奎斯特图上:
幅值裕度(暂时只考虑一次对负实轴的穿越):穿越频率记为 ω c \omega_c ωc,稳定系统要求 ∣ K G ( j ω c ) ∣ < 1 |KG(j\omega_c)|<1 ∣KG(jωc)∣<1,定义GM为(K如果放大GM倍,则系统变得不稳定,化成分贝和Bode图上的定义一致):

相位裕度:当幅值为1时,则曲线穿越单位圆,则是相角与-180之差定义为PM。

②说明
在设计中PM更常用,应为对于标准二阶系统,如果PM小于70,那么有如下关系近似成立( ζ \zeta ζ为阻尼比):

对于标准二阶系统,即使PM大于70,PM增大,也必然会导致系统阻尼增大,从而使得系统的调节时间延长。
![]()
如果GM>0dB,PM>0度,则闭环系统是稳定的。此结论只适用于Nyquist Plot的半闭合曲线只与单位圆和负半实轴相交一次,且系统开环是稳定的,为最小相位系统。
实际中的系统一般都是采用开环Bode Plot的穿越频率(0dB处的频率)来找到对应的PM,反之GM也是 从-180度时的频率找到的。对于non-minimum phase的系统,最好还是要用Nyquist plot来确定其稳定性。PM和GM是相对稳定性的一种表征,也必须两个一起使用才能说明问题。
一般的取值:PM一般为30度到60度之间,GM一般大于6dB。
对于一个一阶系统或者二阶系统而言,相位永远也不会越过180度(即小于-180度),那么GM无穷大,没有参考价值。高阶系统的Bode Plot如果与0dB线多次相交,则上述的定义并不能明确告诉我们哪一个频率下的PM是我们应该取得的。实际上在Nyquist plot中我们都会取GM为最小的值(即最靠近单位圆的交点频率),PM也为最小值,这样保守的估计对设计来讲是安全的。实际中,我们还是会采用Nyquist plot或者Nichols plot来检查GM和PM。
GM 幅值裕度和PM 相位裕度都是用来衡量闭环系统相对稳定性的。两组指标通常需要一起使用才有意义,并且两组指标的数值需要平衡系统的其他性能,因此也并不是在任何时候都是越大越好的。我们在Nyquist plot和Bode plot都能够检查GM和PM的值,但是对于其他不常规的系统,严格的GM和PM还是要通过Nyquist plot或者Nichols plot来确定。
4.5. 根据Bode图设计系统
首先给出一个近似结论:
如果频率特性曲线在该坐标上(如Bode Plot)的一个decade内斜率保持为一个常数n,那么这段曲线对应频率范围内的Phase可以估计为n乘以90度。对于一个积分环节,斜率为-20dB/decade,也就是n=-1。此时的相位为:-1*90°=-90°。
如果我们希望相位裕度为90°,那么显然希望斜率是-1,也就是-20dB/decade,这是我们一般对中频段的要求。
总体来说,我们希望:

开环传递函数低频幅值越大,指令跟踪效果越好,低频扰动抑制能力越好,这就需要较大的穿越频率以及低频段较缓的幅频曲线斜率;
大于截止频率的高频段,幅值越小,对高频噪声的抑制能力越好,这就需要高频段幅频曲线斜率较陡;
中频段则希望是-20db/decade,此时响应速度较快,较稳定。
此外,还需要考虑带宽指标,就是希望截止频率向后移动。总之,各种指标是相互制约的,要找到一个折中。
知乎上有好多大神,多学习学习他们吧。比如lenleo老兄。比如,使用奈奎斯特图是更靠谱的,可以看lenleo老兄的文章。
注意,开环频域指标在一定程度上可以转换为闭环时域指标。
4.6. 闭环系统频域指标
前面论述的所有频域方法的最终目的还是使得闭环系统满足一定的要求,所以有必要对闭环系统的指标进行验证。
闭环系统的频域性能指标有多个:带宽、谐振频率、谐振峰值。
①带宽
闭环系统的频域指标主要指带宽,前面已经介绍过。带宽反映了闭环系统的响应速度,主要影响rise time上升时间。系统带宽扩大n倍,则响应速度加速n倍。带宽大的系统跟踪信号的能力强,因为能在较宽的频率带中跟踪原信号并保持较大的稳态幅值。反过来,因为带宽很大,所以一些高频干扰或者噪音就会被保留甚至放大。因此带宽的选择首先要满足信号跟踪和复现能力,再考虑降低噪音和干扰影响。
为了让系统能够较好地跟踪参考信号reference,系统的带宽应当能覆盖reference的大部分频谱频率。
②谐振频率和谐振峰值
谐振峰值 M r M_r Mr与闭环系统的阻尼比是负相关的,即阻尼比越小,峰值越大。因此峰值的大小是对系统damping的一种指标。
谐振频率 ω r \omega_r ωr是闭环系统瞬态过程响应速度的指标,当阻尼比较小时,谐振频率与有阻尼共振频率,以及自然频率都是近似相等的,所以对应的时域的上升时间rise time就与谐振频率负相关。【谐振频率大,则上升时间缩短】
开环频域指标和闭环频域指标以及时域指标有对应关系:
系统的穿越频率(crossover frequency)我们发现其与闭环系统的带宽bandwidth是有关联的。一般地穿越频率越大,带宽越大。进而影响响应速度。谐振频率一般和穿越频率靠的比较近,因此也可以拿crossover frequency来近似谐振频率。
系统的相位裕度(PM)二阶系统的PM与阻尼比有近似正比关系(当PM不超过60),随后亦有一一对应的关系。PM与超调量和谐振峰值有对应关系,这与PM和阻尼之间的关系也是对应的。我们可以粗略地得出系统的PM值越大则阻尼比越大,超调和谐振峰值越小。
对于时域,则PM可以估计阻尼比,穿越频率可以估计自然频率。
5. 控制器的设计过程
根轨迹方法出现得比较晚,相对于其它方法根轨迹法更直接一些。根轨迹对系统的瞬态(transient)性能有很直接的塑造,因为零极点直接影响了系统性能。调整零极点位置我们能快速实现满足系统的设计。
而采用频域设计方法,我们则关注相位裕度PM,幅值裕度GM,谐振峰值Mr,穿越频率wc,共振频率wr,带宽bandwidth,稳态误差常数。它们包含了动态特性指标和稳态特性指标。
经典控制理论中的设计往往是比较粗糙的,虽然我们根据系统的期望属性能做出控制器(controller)或者补偿器(compensator)的调整,但是我们很多时候却无法精确地在数量上预测调整后的系统性能,需要不断trial and error。更精确的设计还需要现代控制理论解决。
但是,频域设计法在工程中的应用还是十分广泛,尤其是根据Bode Plot来设计。工程中有许多部件的频域信息是比较容易得到的,利用Bode Plot可以把频率特性曲线叠加的特点,可以很方便地把这些部件加入到系统分析中。
超前补偿器设计:
lead compensator基本上就是一个高通滤波器(HPF),其主要调整作用就是在合适的频率附近提高系统的phase,从而增加相角裕度PM,让系统的稳定裕度增大。注意,lead compensator也会让穿越频率少量提高,所以设计时需要考虑多补偿一些相角。
首先定义如下形式的超前补偿器:

极点大于零点,那么相角显然大于零:
![]()
ω = 0 和 ω = ∞ \omega=0和\omega=\infty ω=0和ω=∞的时候, ϕ = 0 \phi=0 ϕ=0,那么显然中间会出现最大相位点,求导可得:


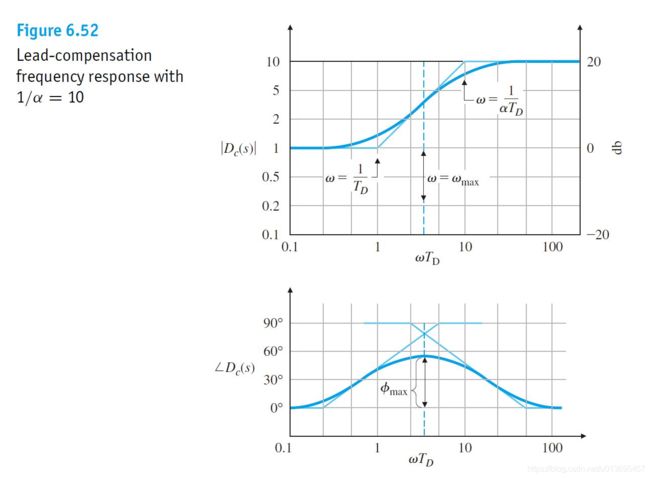
具体设计过程为:
①把compensator化为Bode form,令 K = α K c K=\alpha K_c K=αKc:

有:

其中,
![]()
由于除了 G 1 G_1 G1的部分稳态增益为1,对于单位负反馈,我们直接使用稳态增益公式求得K值:

②画出 G 1 G_1 G1波特图,找到其相角裕度。
③根据对相角裕度的要求,计算差值,差值需要由 T s + 1 α T s + 1 \frac{Ts+1}{\alpha Ts + 1} αTs+1Ts+1补偿,由于超前补偿器会导致一定的幅值抬升,那么我们额外补偿一些相角差值,比如增加个5°,记这个差值为 ϕ m a x \phi_{max} ϕmax。
④根据下式计算 α \alpha α,即我们希望设置补偿器的最大增益在穿越频率附近:
![]()
⑤由于 T T T还没确定,我们把 α \alpha α和:

带入 T s + 1 α T s + 1 \frac{Ts+1}{\alpha Ts + 1} αTs+1Ts+1计算,取模计算最大增益。然后我们在 G 1 G_1 G1上找到该增益的负值数对应的频率,该频率可以作为新的穿越频率 ω m a x \omega_{max} ωmax。那么带入 ω m a x = 1 T a \omega_{max}=\frac{1}{T\sqrt{a}} ωmax=Ta1,即可得到T值。
⑥计算 K c = K α K_c=\frac{K}{\alpha} Kc=αK,画出补偿后的Bode图,检验是否满足指标。不满足则重新设计。
欠缺的内容:Nichols Chart和等M,等N圆这些概念,离散和数字控制。
参考文献
知乎专栏:经典控制理论重点概念 ↩︎