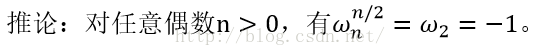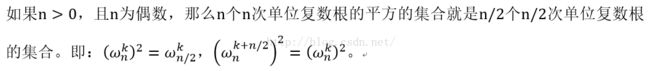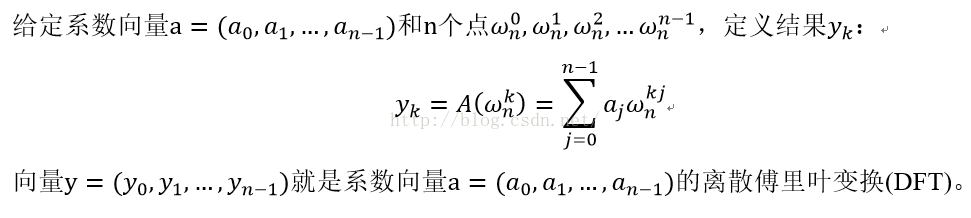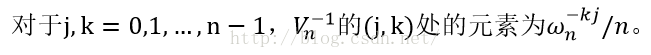数学专题小结：FFT算法

快速傅里叶变换（FFT，Fast Fourier Transform）是信号处理的常用手段，可以把时域信号变成频域信号，时域的卷积运算对应于频域就成了简单的乘法运算。由于两个多项式的乘积，其系数的运算实际上也是一种卷积运算，因此可以用FFT来计算多项式的乘法。网上关于FFT算法的讲解大多都是工程领域的，这里从算法竞赛的角度来剖析一下怎么简洁而高效的实现FFT。

一，为什么要用FFT来计算多项式乘法

众所周知，如果我们用普通的for循环来直接计算系数的话，算法的时间复杂度是O(N^2)级别的，算法慢的原因是因为我们是在用系数表达式计算的。而实际上，还有另外一种方法也可以完整的表达一个多项式，那就是点值表达式。通俗的说就是给出n个不同的Xi，求出对应的Yi，那么这n对(Xi,Yi)就可以准确的确定一个多项式的系数。那么如何通过点值表达式计算多项式相乘的系数呢？首先，我们计算得到n个A(Xi)和n个B(Xi)，那么A(Xi)*B(Xi)就是多项式相乘后在Xi处的结果，这样就有n个A(Xi)B(Xi)，可以唯一的确定一个多项式。然而，如果只是随意的选择n个点，计算出这n个点值的时间复杂度仍然是O(N^2)的，并没有丝毫改善。但是，如果我们巧妙的选取这n个点，就可以加速这一计算过程，使得计算出这n个点的时间复杂度降为O(NlogN)。这n个点就是n次单位复数根对应的点。

二，n次单位复数根的性质

FFT算法之所以可以很快就是利用了n次单位根的性质来加速计算的。下面就是用到的3条性质。

1. 消去引理

它的一个推论如下：

2.折半引理

它的一个推论如下：

3.求和引理

以上三个引理，这里不做证明了，读者可以通过n次单位根的定义不难得证。下面主要来谈一谈这3个定理是如何加速n个点值的计算的。

三，DFT和FFT

DFT的定义如下：

由DFT的定义不难发现，实际上就是计算n个n次单位复数根处的y值。经过DFT变换就可以得到n个点值了。而FFT就是利用n次单位复数根的性质来加速DFT计算的一种方法。

四，FFT的分治策略

FFT采用了分治策略，它将一个多项式拆成2部分，下标为偶数部分构成的多项式A0(x)和下标为奇数部分构成的多项式A1(x)，那么计算A(x)具体来说如下：

根据折半引理，上述的n个取值只有n/2个是不相同的，因此我们可以递归地对次数为n/2的2个多项式在n/2个根处进行求值，此时问题和原问题相同，但是规模缩小了一半。

五，利用迭代法实现的FFT

假设我们已经求解完子问题，那么就该用第3个等式来对结果进行合并，具体合并方式用伪代码描述如下：

for k=0 to n/2-1
    t=w*y0[k]
    y[k]=y0[k]+t
    y[k+(n/2)]=y0[k]-t
    w=w*wn

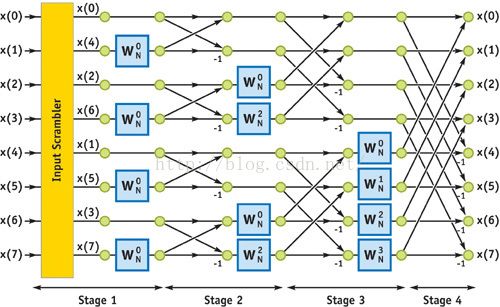
上面的伪代码中for语句下面的前3步被称为是蝴蝶操作，它的作用在这里极其重要，可以用下面的图来表示：

上图中，每一个交叉位置都是一次蝴蝶操作，计算出的2个中间结果，是下一次蝴蝶操作的基础，从上图还不难发现一个事实：只有logN层计算，每一层用到的w值都是相同的，由于总共只输入了N个值，因此我们总共只计算了O(NlogN)次蝴蝶操作就算出了所有的y值。这就是为什么FFT的时间复杂度是O(NlogN)的原因了。

如果仔细观察，还会发现一个问题：第一次蝴蝶操作用到的2个操作数并不相邻，然而我们输入的却是x0,x1,...,xn-1，怎样才能快速变成蝴蝶操作需要的排列呢？实际上，FFT的分治策略中已经提到过，是吧下标按照奇偶性分成了2个子多项式，那么，如果我们继续分下去，直到只有一个元素时候停止，把所有的元素按照顺序排成一列，就是上图中的顺序。比如:序列0,1,2,3,4,5,6,7第一次操作完变成0,2,4,6,1,3,5,7，第二次操作完变成0,4,2,6,1,5,3,7。和上图一样了。这种置换被称为位逆序置换(Bit Reversal)。那么怎么快速实现这一操作呢？观察这些数的二进制形式

我们观察标记为红色的1的变化，可以发现如下的规律：如果当前j的最高位的前一位是1，那么就把这个1给变为0，然后继续检查下一位是否为1，如果是，继续变为0，直到没有连续的1为止，然后把刚好没有1的位置变为1；否则，就把最高位的下一位变成1。这样就得到了生成下一个j的算法，代码如下：

for(int i = 0, j = 0; i < n; i++) 
  {
    if(j > i) swap(a[i], a[j]);
    int k = n;
    while(j & (k >>= 1)) j &= ~k;
    j |= k;
  }

最后，得到了n个点值后，如何恢复出系数呢？答案是利用逆矩阵来求系数，因为这n个点值写成矩阵的计算形式如下：

可以看出，这个矩阵的系数矩阵V是一个范德蒙德矩阵，它的逆一定存在，而且可以证明，每个元素的逆等于下式：

这样，就可以顺利恢复出最终的系数了。

六，FFT算法具体实现

FFT加速多项式相乘具体过程如下：

（1）补0：在2个多项式的最高次前面补0，得到两个2n次的多项式，设系数向量分别为v1,v2。

（2）求值：用FFT计算f1=DFT(v1),f2=DFT(v2)。这里得到的f1,f2就是上面所说的n个点值。

（3）乘法：把两个向量f1,f2的每一维对应相乘，得到向量f，它对应两个多项式乘积的点值表示。

（5）插值：用FFT计算v=IDFT(f)，其中v就是乘积的系数向量。

下面直接给出一份简洁而高效的FFT算法实现的代码和利用FFT加速多项式相乘的实现过程

const double PI = acos(-1.0);

typedef complex CD;

// Cooley-Tukey的FFT算法，迭代实现。inverse = false时计算逆FFT
inline void FFT(vector &a, bool inverse) 
{
	int n = a.size();
	for (int i = 0, j = 0; i < n; i++) // 原地快速bit reversal
	{
		if (j > i) swap(a[i], a[j]);
		int k = n;
		while (j & (k >>= 1)) j &= ~k;
		j |= k;
	}

	double pi = inverse ? -PI : PI;
	for (int step = 1; step < n; step <<= 1) 
	{    // 把每相邻两个“step点DFT”通过一系列蝴蝶操作合并为一个“2*step点DFT”
		double alpha = pi / step;
		// 为求高效，我们并不是依次执行各个完整的DFT合并，而是枚举下标k
		// 对于一个下标k，执行所有DFT合并中该下标对应的蝴蝶操作，即通过E[k]和O[k]计算X[k]
		// 蝴蝶操作参考：http://en.wikipedia.org/wiki/Butterfly_diagram
		for (int k = 0; k < step; k++) 
		{   // 计算omega^k. 这个方法效率低，但如果用每次乘omega的方法递推会有精度问题。
			// 有更快更精确的递推方法，为了清晰起见这里略去
			CD omegak = exp(CD(0, alpha*k));
			for (int Ek = k; Ek < n; Ek += step << 1) 
			{                        // Ek是某次DFT合并中E[k]在原始序列中的下标
				int Ok = Ek + step; // Ok是该DFT合并中O[k]在原始序列中的下标
				CD t = omegak * a[Ok]; // 蝴蝶操作：x1 * omega^k
				a[Ok] = a[Ek] - t;  // 蝴蝶操作：y1 = x0 - t
				a[Ek] += t;         // 蝴蝶操作：y0 = x0 + t
			}
		}
	}
	if (inverse)
		for (int i = 0; i < n; i++) a[i] /= n;
}

// 用FFT实现的快速多项式乘法
inline vector operator * (const vector& v1, const vector& v2) 
{
	int s1 = v1.size(), s2 = v2.size(), S = 2;
	while (S < s1 + s2) S <<= 1;
	vector a(S, 0), b(S, 0); // 把FFT的输入长度补成2的幂，不小于v1和v2的长度之和
	for (int i = 0; i < s1; i++) a[i] = v1[i];
	FFT(a, false);
	for (int i = 0; i < s2; i++) b[i] = v2[i];
	FFT(b, false);
	for (int i = 0; i < S; i++) a[i] *= b[i];
	FFT(a, true);
	vector res(s1 + s2 - 1);
	for (int i = 0; i < s1 + s2 - 1; i++) res[i] = a[i].real(); // 虚部均为0
	return res;
}