CTC解决什么问题
CTC,Connectionist Temporal Classification,用来解决输入序列和输出序列难以一一对应的问题。
举例来说,在语音识别中,我们希望音频中的音素和翻译后的字符可以一一对应,这是训练时一个很天然的想法。但是要对齐是一件很困难的事,如下图所示(图源见参考资料[1]),有人说话块,有人说话慢,每个人说话快慢不同,不可能手动地对音素和字符对齐,这样太耗时。
再比如,在OCR中使用RNN时,RNN的每一个输出要对应到字符图像中的每一个位置,要手工做这样的标记工作量太大,而且图像中的字符数量不同,字体样式不同,大小不同,导致输出不一定能和每个字符一一对应。
CTC基本概述
考虑一个LSTM,用w表示LSTM的参数,则LSTM可以表示为一个函数:\(y = N_w(x)\)。
定义输入x的时间步为T,每个时间步上的特征维度记作m,表示m维特征。
\[ x = (x^1, x^2, ..., x^T) \\x^t = (x_1^t, x_2^t, ..., x_m^t)\]
输出时间步也为T,和输入可以一一对应,每个时间步的输出维度作为n,表示n维输出,实际上是n个概率。
\[ y = (y^1, y^2, ..., y^T) \\y^t = (y_1^t, y_2^t, ..., y_n^t)\]
假设要对26个英文字符进行识别,考虑到有些位置没有字符,定义一个-作为空白符加入到字符集合\({L}'= \{a,b,c,...,x,y,z\} \cup \{-\}= L \cup \{-\} = \{a,b,c,...,x,y,z,-\}\),那么对于LSTM而言每个时间步的输出维度n就是27,表示27个字符在这个时间步上输出的概率。
如果根据这些概率进行选取,每个时间步选取一个元素,就可以得到输出序列,其输出空间可以记为\({L}'^T\)。
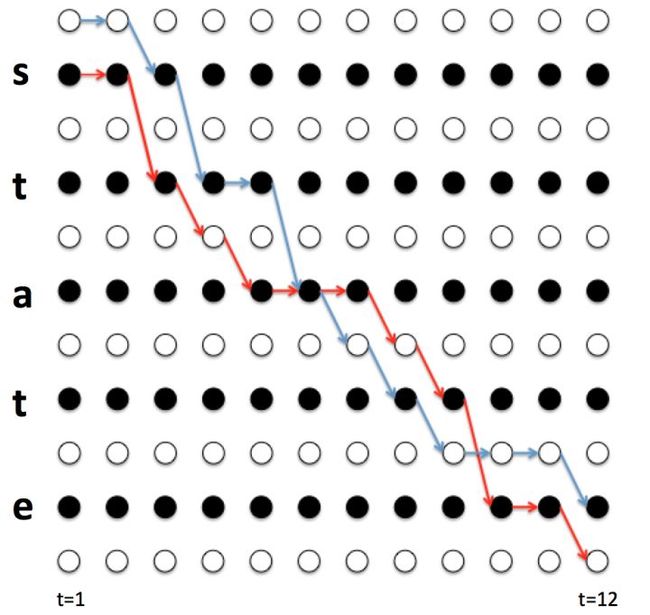
定义一个B变换,对LSTM的输出序列(比如下例中的4个\(\pi\))进行变换,变换成真实输出(比如下例中的state),把连续的相同字符删减为1个并删去空白符。举例说明,当T=12时:
\[\begin{split} B(\pi^1) &= B(--stta-t---e) = state \\ B(\pi^2) &= B(sst-aaa-tee-) = state \\ B(\pi^3) &= B(--sttaa-tee-) = state \\ B(\pi^4) &= B(sst-aa-t---e) = state \end{split}\]
其中\(\pi\)表示LSTM的一种输出序列。当我们优化LSTM时,只需要最大化以下概率,即给定输入x的情况下,输出为l的概率,\(l\)表示真实输出。对下式取负号,就可以使用梯度下降对其求最小。
\[p(l \ | \ x) = \sum_{B(\pi)=l} p(\pi | x)\]
假设时间步之间的输出独立,那么对于任意一个输出序列\(\pi\)的概率计算式子如下,
\[p(\pi | x) = \prod_{t=1}^{T} y_{\pi_t}^t\]
其中下标\(\pi_t\)表示的是,输出序列在t时间步选取的元素对应的索引,比如该序列在第一个时间步选取的元素是a,那么得到的值就是1。选取的是z,那么得到的值就是26。选取的是空白符,那么得到的值就是27。为了方便观测,也用对应的字符表示,其实是一个意思,如下式所示。
\[ \pi = (--stta-t---e) \\ p(\pi | x) = {y^1}_{-} \cdot {y^2}_{-} \cdot y^3_{s} \cdot y^4_{t} \cdot y^5_{t} \cdot y^6_{a} \cdot {y^7}_{-} \cdot {y^8}_{t} \cdot {y^9}_{-} \cdot {y^{10}}_{-} \cdot {y^{11}}_{-} \cdot y^{12}_{e} \]
但是对于某一个真实输出,比如上述的state,有多个LSTM的输出序列可以通过B转换得到。这些序列都是我们要的结果,我们要使给定x,这些输出序列的概率加起来最大。如果逐条遍历来求得,时间复杂度是指数级的,因为有T个位置,每个位置有n种选择(字符集合的大小),那么就有\(n^T\)种可能。因此CTC借用了HMM中的“前向-后向算法”(forward-backward algorithm)来计算。
CTC中的前向后向算法
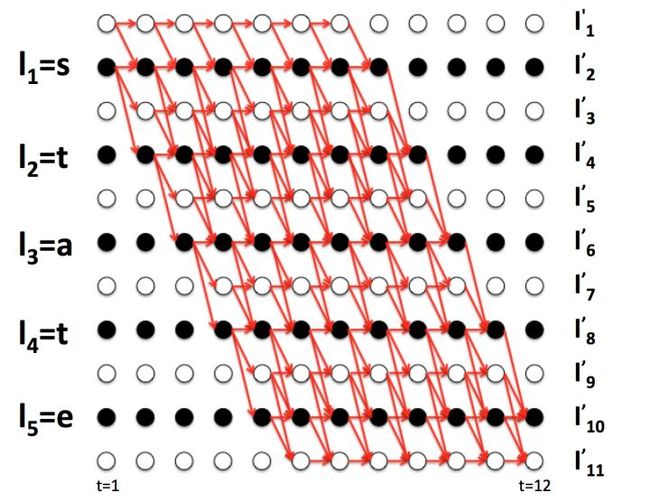
由于真实输出\(l\)是一个序列,序列可以通过一个路径图中的一条路径来表示,我们也称输出序列\(l\)为路径\(l\)。定义路径\({l}'\)为“在路径\(l\)每两个元素之间以及头尾插入空白符”,如:
\[l = state \\ {l}' = -s-t-a-t-e-\]
对某个时间步的某个字符求导(这里用k表示字符集合中的某个字符或字符索引),恰好是与概率\(y_k^t\)相关的路径。
\[ \frac{\partial \, p(l \ |x)}{\partial \, y_k^t} = \frac{\partial \, \sum_{B(\pi)=l, \pi_t=k} p(\pi | x)}{\partial \, y_k^t} \]
以前面的\(\pi^1, \pi^2, \pi^3, \pi^4\)为例子,画出两条路径(还有两条没画出来),如下图所示(图源见参考资料[1])。
4条路径都在t=6时经过了字符a,观察4条路径,可以得到如下式子。
\[ \begin{split} \pi^1 &= b = b_{1:5} + a_6 + b_{7:12} \\ \pi^2 &= r = r_{1:5} + a_6 + r_{7:12} \\ \pi^3 &= b_{1:5} + a_6 + r_{7:12} \\ \pi^4 &= r_{1:5} + a_6 + b_{7:12} \end{split}\]
\[\begin{split} p( \pi^1, \pi^2, \pi^3, \pi^4 | x) &= {y^1}_{-} \cdot {y^2}_{-} \cdot {y^3}_{s} \cdot {y^4}_{t} \cdot {y^5}_{t} \cdot {y^6}_{a} \cdot {y^7}_{-} \cdot {y^8}_{t} \cdot {y^9}_{-} \cdot {y^{10}}_{-} \cdot {y^{11}}_{-} \cdot {y^{12}}_{e} \\ &+ {y^1}_{s} \cdot {y^2}_{s} \cdot {y^3}_{t} \cdot {y^4}_{-} \cdot {y^5}_{a} \cdot {y^6}_{a} \cdot {y^7}_{a} \cdot {y^8}_{-} \cdot {y^9}_{t} \cdot {y^{10}}_{e} \cdot {y^{11}}_{e} \cdot {y^{12}}_{-} \\ &+ {y^1}_{-} \cdot {y^2}_{-} \cdot {y^3}_{s} \cdot {y^4}_{t} \cdot {y^5}_{t} \cdot {y^6}_{a} \cdot {y^7}_{a} \cdot {y^8}_{-} \cdot {y^9}_{t} \cdot {y^{10}}_{e} \cdot {y^{11}}_{e} \cdot {y^{12}}_{-} \\ &+ {y^1}_{s} \cdot {y^2}_{s} \cdot {y^3}_{t} \cdot {y^4}_{-} \cdot {y^5}_{a} \cdot {y^6}_{a} \cdot {y^7}_{-} \cdot {y^8}_{t} \cdot {y^9}_{-} \cdot {y^{10}}_{-} \cdot {y^{11}}_{-} \cdot {y^{12}}_{e}\end{split}\]
令:
\[\begin{split} forward &= p(b_{1:5} + r_{1:5} | x) = {y^1}_{-} \cdot {y^2}_{-} \cdot {y^3}_{s} \cdot {y^4}_{t} \cdot {y^5}_{t} + {y^1}_{s} \cdot {y^2}_{s} \cdot {y^3}_{t} \cdot {y^4}_{-} \cdot {y^5}_{a} \\ backward &= p(b_{7:12} + r_{7:12} | x) = {y^7}_{-} \cdot {y^8}_{t} \cdot {y^9}_{-} \cdot {y^{10}}_{-} \cdot {y^{11}}_{-} \cdot {y^{12}}_{e} + {y^7}_{a} \cdot {y^8}_{-} \cdot {y^9}_{t} \cdot {y^{10}}_{e} \cdot {y^{11}}_{e} \cdot {y^{12}}_{-} \end{split}\]
那么可以做如下表示:
\[p( \pi^1, \pi^2, \pi^3, \pi^4 | x) = forward \cdot y_a^t \cdot backward\]
上述的forward和backward只包含了4条路径,如果推广一下forward和backward的含义,考虑所有路径,可做如下表示:
\[\sum_{B(\pi)=l, \pi_6=a} p(\pi | x) = forward \cdot y_a^t \cdot backward\]
定义forward为\(\alpha_t({l}'_k)\),表示t时刻经过\({l}'_k\)字符的路径概率中1-t的概率之和,式子定义如下。
\[\alpha_t({l}'_k) = \sum_{B(\pi)=l, \ \pi_t = {l}'_k} \ \prod_{{t}'=1}^{t} {y_{\pi_{{t}'}}^{{t}'}}\]
t=1时,符号只能是空白符或\(l_1\),可以得到以下初始条件:
\[\alpha_1(-) = {y^1}_{-} \\ \alpha_1(l_1) = y^1_{l_1} \\ \alpha_1(l_t) = 0, \forall t > 1 \]
观察上图((图源见参考资料[1])可以发现,如果t=6时字符是a,那么t=5时只能是字符a,t,空白符三选一,否则经过B变换后无法得到state。
可以得到以下递推关系:
\[\alpha_6(a) = (\alpha_5(a) + \alpha_5(t) + \alpha_5(-)) \cdot y_a^6\]
更一般地,可以得到如下递推关系:
\[\alpha_t({l}'_k) = (\alpha_{t-1}({l}'_k) + \alpha_{t-1}({l}'_{k-1}) + \alpha_{t-1}(-)) \cdot y_{{l}'_k}^t\]
定义backward为为\(\beta_t(s)\),表示t时刻经过\({l}'_k\)字符的路径概率中t-T的概率之和,式子定义如下。
\[\beta_t({l}'_k) = \sum_{B(\pi)=l, \ \pi_t = {l}'_k} \ \prod_{{t}'=t}^{T} {y_{\pi_{{t}'}}^{{t}'}}\]
t=T时,符号只能是空白符或\(l_{|{l}'|-1}\),可以得到以下初始条件:
\[\beta_T(-) = {y^T}_- \\ \beta_T({l}'_{|{l}'|-1}) = y^T_{l_{|{l}'|-1}} \\ \beta_T(l_{|{l}'|-i}) = 0, \forall i > 1 \]
同理,可以得到如下递推关系:
\[\beta_t({l}'_k) = (\beta_{t+1}({l}'_k) + \beta_{t+1}({l}'_{k+1}) + \beta_{t+1}(-)) \cdot y_{{l}'_k}^t\]
根据forward和backward的式子定义,它们相乘可以得到:
\[\alpha_t({l}'_k) \beta_t({l}'_k) = \sum_{B(\pi)=l, \ \pi_t = {l}'_k} \ y_{{l}'_k}^t \prod_{t=1}^{T} {y_{\pi_t}^t}\]
又因为\(p(l \ | \ x)\) 对\({l}'_k\)求导时,只跟那些\(\pi_t = {l}'_k\)的路径有关,那么求导时(注意是求导时)可以简写如下式子:
\[p(l \ | \ x) = \sum_{B(\pi)=l, \ \pi_t = {l}'_k} p(\pi | x) = \sum_{B(\pi)=l, \ \pi_t = {l}'_k} \ \prod_{t=1}^{T} y_{\pi_t}^t\]
结合上面两式,得到:
\[p(l \ | \ x) = \sum_{B(\pi)=l, \ \pi_t = {l}'_k} \ \frac{\alpha_t({l}'_k) \beta_t({l}'_k) }{y_{{l}'_k}^t}\]
最后可以得到求导式(这里用k来表示字符,和\({l}'_k\)的含义相同):
\[\frac{\partial \, p(l \ |x)}{\partial \, y_k^t} = \frac{\partial \ \sum_{B(\pi)=l, \ \pi_t = k} \frac{\alpha_t(k) \beta_t(k) }{y_k^t}}{\partial \, y_k^t}\]
求导式里的forward和backward可以用前面的dp递推式计算出来,时间复杂度是\(nT\),相比于前面的指数复杂度\(n^T\)大大减小了计算量。
这样对LSTM的输出y求导之后,再根据y对LSTM里面的权重参数w进行链式求导,就可以使用梯度下降的方法来更新参数了。
CTC的预测
一种方法是Best Path search。计算概率最大的一条输出序列(假设时间步独立,那么直接在每个时间步取概率最大的字符输出即可),但是这样没有考虑多个输出序列对应一个真实输出这件事,举个例子,[s,s,-]和[s,s,s]的概率比[s,t,a]低,但是它们的概率之和会高于[s,t,a]。
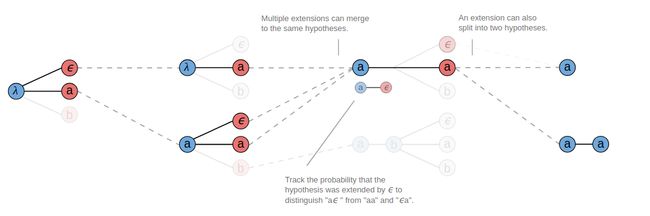
第二种方法是Beam Search。假设指定B=3,预测过程如下图所示(图源见参考资料[2])。在第一个时间步选取概率最大的三个字符,然后在第二个时间步也选取概率最大的三个字符,两两组合(概率相乘)可以组合成9个序列,这些序列在B转换之后会得到一些相同输出,把具有相同输出的序列进行合并,比如有3个序列都可以转换成a,把它们合并(概率加在一起),计算出概率最大的三个序列,然后继续和下一个时间步的字符进行同样的合并。
有一点需要注意的是合并相同字符时,比如我们看上图T=3的时候,第一个前缀序列a,在跟相同字符a合并的时候,除了产生a之外,还会产生一个aa的有效输出。这是因为这个前缀序列a在T=2的时候曾经是把空白符合并掉了,实际上这个前缀序列a后面是跟着一个空白符的,所以它在跟相同字符a合并的时候中间是有一个隐藏的空白符,合并之后得到的应该是两个a。
因此在合并相同字符时,如果要合并成aa,需要统计在这之前以空白符结尾的那些序列的概率,如果要合并成a,计算的是不以空白符结尾的那些序列的概率。出于这个事实,我们需要跟踪前两处输出,以便于后续的合并计算,见下图所示(图源见参考资料[2])。
CTC的几个性质
第一个是条件独立性。CTC做了一个假设就是不同时间步的输出之间是独立的。这个假设对于很多序列问题来说并不成立,输出序列之间往往存在联系。
第二个是单调对齐。CTC只允许单调对齐,在语音识别中可能是有效的,但是在机器翻译中,比如目标语句中的一些比较后的词,可能与源语句中前面的一些词对应,这个CTC是没法做到的。
第三个是多对一映射。CTC的输入和输出是多对一的关系。这意味着输出长度不能超过输入长度,这在手写字体识别或者语音中不是什么问题,因为通常输入都会大于输出,但是对于输出长度大于输入长度的问题CTC就无法处理了。
参考资料
[1] 知乎上的一篇文章:一文读懂CRNN+CTC文字识别
[2] Distill上一篇关于CTC的介绍(作者Hannun Awni):Sequence Modeling With CTC