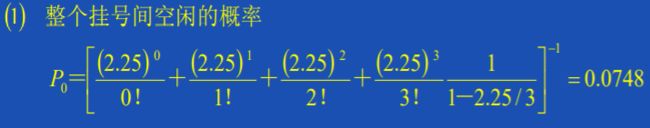排队论 （queuing theory）推论与举例
目录
1、排队模型的表示
2、排队系统的衡量指标
3、排队系统的要素
顾客的输入过程
排队结构与排队规则
服务机构与服务规则
其中，到达间隔和服务时间（X，Y）具有的典型分布有
4、模型的系统运行状态参数：
泊松流到达间隔服从负指数分布：
顾客服务时间分布（负指数分布）:
5、M/M/1模型：
1、模型的条件是：
2、对于M/M/1模型有如下公式：
3、举例
6、M/M/S模型
1、模型的条件是：
2、对应M/M/S有如下公式：
3、举例
排队论 (queuing theory)，或称随机服务系统理论， 是通过对服务对象到来及服务时间的统计研究，得出这些数量指标（等待时间、排队长度、忙期长短等）的统计规律，然后根据这些规律来改进服务系统的结构或重新组织被服务对象，使得服务系统既能满足服务对象的需要，又能使机构的费用最经济或某些指标最优。它是数学运筹学的分支学科，也是研究服务系统中排队现象随机规律的学科。广泛应用于计算机网络、生产、运输、库存等各项资源共享的随机服务系统。 排队论研究的内容有 3 个方面：统计推断，根据资料建立模型；系统的性态，即和排队有关的数量指标的概率规律性；系统的优化问题。其目的是正确设计和有效运行各个服务系统，使之发挥最佳效益。
最初是用 3 个字母组成的符号 X/Y/Z 表示一个排队系统。其中 X 表示顾客到达时间分布，Y 表示服务时间的分布，Z 表示服务机构中的服务台的个数
1、排队模型的表示
X/Y/Z/A/B/C
X — 顾客相继到达的间隔时间的分布；
Y — 服务时间的分布(M — 负指数分布、D — 确定时间、Ek — k 阶埃尔朗分布、G — 一般随机分布、GI—一般相互独立分布)
Z — 服务台个数；
A — 系统容量限制（默认为 ∞）；
B — 顾客源数目（默认为 ∞）；
C — 服务规则 （默认为先到先服务 FCFS）。
2、排队系统的衡量指标
服务队长 Ls — 正在接受服务的顾客数；期望值；
排队长 Lq — 在队列中等待的顾客数；期望值；
总队长 L = Ls + Lq — 系统中的顾客总数；期望值；
服务时间 E — 顾客在服务中消耗的时间；期望值；
等待时间 Wq — 顾客在队列中等待的时间；期望值；
总时间 Ws = E + Wq — 顾客在系统中的总逗留时间；期望值
忙期 — 服务机构两次空闲的时间间隔；
稳态 — 系统运行充分长时间后，初始状态的影响基本消失，系统状态不再随时间变化。
服务强度 ：
；
3、排队系统的要素
（1）顾客输入过程；
（2）排队结构与排队规则；
（3）服务机构与服务规则。
-
顾客的输入过程
顾客源(总体)：有限/无限;
顾客到达方式：逐个/逐批;(仅研究逐个情形)
顾客到达间隔：随机型/确定型; <<<< X
顾客前后到达是否独立：相互独立/相互关联；
输入过程是否平稳：平稳/非平稳；(仅研究平稳性)
注：其中顾客到达间隔满足如下条件,则称为泊松流（满足泊松分布）：
(1) 在不相互重叠的时间区间内，到达顾客数相互独立(无后效性)；
(2) 对于充分小的时间间隔![\left [ t,t+\Delta t \right ]](http://img.e-com-net.com/image/info8/3b14675587694a8f8e6da5d56b26c1ad.gif){kind=small}
内，到达1个顾客的概率与t无关，仅与时间间隔成正比 (平稳性) ；
(3) 对于充分小的时间间隔，2个及以上顾客到达的概率可忽略不计 (普通性)。
-
排队结构与排队规则
顾客排队方式：等待制/即时制(损失制);
排队系统容量：有限制/无限制;
排队队列数目: 单列/多列;
是否中途退出: 允许/禁止;
是否列间转移: 允许/禁止; (仅研究禁止退出和转移的情形)
-
服务机构与服务规则
服务台(员)数目;单个/多个; <<<< Z
服务台(员)排列形式;并列/串列/混合;
服务台(员)服务方式;逐个/逐批;(研究逐个情形)
服务时间分布;随机型/确定型; <<<< Y
服务时间分布是否平稳:平稳/非平稳;(研究平稳情形)
其中，到达间隔和服务时间（X，Y）具有的典型分布有：
| 泊松分布 | M |
| 负指数分布 | M |
| k阶爱尔朗分布 | Ek |
| 确定型分布 | D |
| 一般服务时间分布 | G |
归纳以上可得，经典排队系统模型（X，Y，Z，A，B，C）可表示成为：
- M/M/1，M/D/1，M/ Ek /1
- M/M/c， M/M/c/∞/m，
- M/M/c/N/∞ ，。。。
注：
，M、D为上述几种分布。
4、模型的系统运行状态参数：
系统状态 N(t) —— 指排队系统在时刻t时的全部顾客数N(t)， 包括“排队顾客数”（Lq）和“正被服务顾客数”（Ls）；
系统状态概率：
(1)瞬态概率Pn(t)
——表示时刻t系统状态 N(t)=n 的概率（也就是顾客到达数为n的概率分布）;
(2)稳态概率Pn
—— 
——一般排队系统运行了一定长的时间后，系统状态的概率分布不再随时间 t变化，即初始时刻（t=0）系统状态的概率分布 (Pn(0) ，n>>0）的影响将消失。
公式推导过程：
总结上述
可知泊松流到达间隔服从负指数分布：
- 若顾客到达间隔T的概率密度为
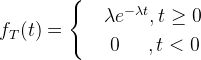
则成T服从负指数分布，分布函数为：
- 若顾客流是泊松流时，顾客到达的时间间隔服从上述负指数分布。
- 其中，E[T]=1/λ ; Var [T]=1/λ2 ; σ [T]=1/λ
- λ 为单位时间顾客到达数的期望，称为平均到达率；1/λ 为平均间隔时间。
顾客服务时间分布（负指数分布）
- 对一个顾客的服务时间Ts，等价于相邻两个顾客离开排队系统的时间间隔。若Ts服从负指数分布，其概率密度函数为：
分布函数为：
则 E[Ts]=1/µ ; Var [Ts]=1/ µ 2 ; σ [Ts]=1/ µ - E[Ts]=1/µ ：每个顾客的平均(期望)服务时间； µ:单位时间服务的顾客数，平均(期望)服务率；
- 其中μ 为平均服务率，1/μ 为平均服务时间。
5、M/M/1模型：
1、模型的条件是：
1、输入过程――顾客源是无限的，顾客到达完全是随机的，单个到来，到达过程服从泊松分布，且是平稳的；
2、排队规则――单队，且队长没有限制，先到先服务；
3、服务机构――单服务台，服务时间的长短是随机的，服从相同的指数分布 。
2、对于M／M／1模型有如下公式：
 |
 |
 |
 |
 |
 |
注：（橙色标注为可做评价类指标）
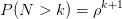：N>k的概率为P；- N(t)：系统顾客数；
- P0：系统处于没有顾客来到要求服务的概率
- 系统负荷水平 ρ ：它是衡量服务台在承担服务和满足需要方面能力的尺度；
- 总队长Ls：系统中排队等待服务和正在服务的顾客总数，其平均值；
- 队长Lg：系统中排队等待服务的顾客数，其平均值；
- 逗留时间Ws：一个顾客在系统中停留时间，包括等待时间和服务时间，其平均值；
- 等待时间Wg：一个顾客在系统中排队等待时间，其平均值。
- λ为平均到达率，1/λ 为平均间隔时间；
μ为平均服务率，1/μ 为平均服务时间。
3、举例
某医院急诊室同时只能诊治一个病人，诊治时间服从指数分布，每个病人平均需要15分钟。病人按泊松分布到达，平均每小时到达3人。试对此排队队系统进行分析。
（1）先确定参数值：这是单服务台系统，有：
λ=3人/h µ =60/15=4人/h
故服务强度为：
（2）计算稳态概率：P0=1-ρ，也就是急诊室空闲的概率；
繁忙的概率服从二项分布：ρ=1-P0=0.75
（3）急症室总病人数平均值：
急症室排队等待人数：
病人在急症室逗留时间：
病人平均等候时间：
6、M/M/S模型
1、模型的条件是：
- 此模型与M/M/1模型不同之处在于有S个服务台， 各服务台的工作相互独立，服务率相等，如果顾客到达时，S个服务台都忙着，则排成一队等待，先到先得（FCFS）服务的单队模型；
- 可以看做是s个M/M/1模型组合。
- 整个系统的平均服务率为sμ，ρ*＝λ/sμ，（ρ*<1）为该系统的服务强度。
2、对应M/M/S有如下公式：
（1）状态概率：
![\large P_{0}=\left [ \sum_{k=0}^{s-1}\frac{1}{k!} (\frac{\lambda}{\mu})^{k}+\frac{1}{s!}\frac{1}{1-\rho^{*}}(\frac{\lambda}{\mu})^{s}\right ]^{-1}](http://img.e-com-net.com/image/info8/c64bf5c7a3c1441ba206ed8a0ed77081.gif)
（2）主要运行指标：
（3）系统状态
的概率：
3、举例
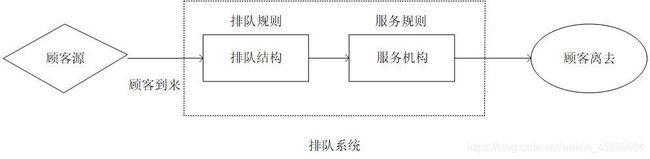
某医院挂号室有三个窗口，就诊者的到达服从泊松分布，平均到达率为每分钟0.9人，挂号员服务时间服从指数分布，平均服务率每分钟0.4人，现假设就诊者到达后排成一队，依次向空闲的窗口挂号，显然系统的容量和顾客源是不限的，属于M/M/S型的排队服务模型。求：该系统的运行指标：Po、Lq、L、W、Wq、P(N≥3)。
由题可得：s=3；λ=0.9人/min；μ=0.4人/min；
ρ=0.9/0.4=2.25；ρ*＝λ/sμ=ρ/s=2.25/3=3/4
代入上列公式可得：Po、Lq、L、W、Wq、P。
