SDAE训练流程和代码实现(Matlab)——咬文嚼字系列

    SDAE（stacked denoised autoencoder ，堆栈去噪自编码器）是vincent大神提出的无监督的神经网络模型，论文：Stacked Denoising Autoencoders: Learning Useful Representations ina Deep Network with a Local Denoising Criterion，原文作者从不同角度解释了模型架构设计理念，非常值得一读。原文请戳：http://www.jmlr.org/papers/volume11/vincent10a/vincent10a.pdf

        先介绍SDAE的主要流程，如下图。x是输入的信号，对x增加了一些噪声后得到x'，下图中加噪声的方法是舍弃了几个神经元，即神经元随机置0，然后进行矩阵变换 [图中f] 得到y，对y再进行矩阵变换 [图中g] 得到z，损失函数就是原始信号x和z之间的距离，我们希望这个距离越小越好，可以用二范数度量或者其他。

   

为什么说SDAE是无监督任务？

       有监督方法需要有输入信号对应的标签，比如图像分类任务有整幅图对应的标签，语义分割任务有图中每个像素对应的标签，比如最经典的数字分类网络lenet5，需要知道每幅图对应的数字是几。无监督任务是不需要标签的， 从fig1我们可以看到，输入信号只有x，我们已知的信息只有x，加入x是二维图像的话，没有这幅图的任何标签信息。所以说SDAE是无监督的。

 

    本文SDAE针对图像进行训练，模型的输入是图像每个像素位置5*5的邻域块共25个元素。

    SDAE网络训练的总流程如图1所示，后面逐一对三个步骤进行详细介绍

图1： SDAE网络训练总流程图

一、数据预处理

1，函数：uniform_sampling.m

patchsize =5; % window size;

[patches_1,patches_2]= uniform_sampling(im1,im2,patchsize);

上面函数中patchsize是采样窗大小，可自行设置这里设置为5；输入的im1和im2分别为时相1图像和时相2图像，假设输入的都是Bern图像，im1和im2大小分别是301*301，对每个像素采样选择以该像素为中心的5*5邻域像素值，则每个像素对应25维向量，则im1和im2变成了301*301*25的三维向量，再将前两维转变为1维，则im1和im2的大小都变成了90601*25. 令patches_1=im1，大小为90601*25，令patches_2=im2，大小为90601*25

数据预处理的流程如下：

Im1数据预处理如图2所示，Im2和im1处理方法相同。

图2 数据预处理

二、SDAE网络训练

 pre-training

1，网络结构初始化

函数saesetup.m ；nnsetup.m;

SDAE输入的是patches_1和patches_2，是25维数据，中间隐层设置为100维，输出是20维，所以网络结构是25——>100——>20，pre-training的时候是每次只训练一层，每层都作为一个去噪自编码器训练，然后训练完了一层再训练下一层；回忆下自编码器的流程，希望输入X和输出Z是一致的，然后通过最小化输入和输出的误差L(X,Z)来求权重W，所以这里需初始化两个网络。

第一层的网络结构是25——>100——>25，初始化的权重分别记为sae.ae{1}W{1}：100*26 ，sae.ae{1}W{2}：25*101; 其中ae{1}是指第一层网络,W{1}是从25映射到100需要的权重，W{2}是从100映射到25需要的权重。

第二层的网络结构是100——>20——>100，初始化的权重分别记为sae.ae{2}W{1}：20*101，sae.ae{2}W{1}：100*21; 其中ae{2}是指第一层网络,W{1}是从100映射到20需要的权重, W{2}是从20映射到100需要的权重.

除了权重W，还有权重变化量vW需要初始化，vW用来梯度下降法时更新W，还有其他一些参数需要初始化activation_function，learningRate等，等下面用到再做具体介绍。

2，训练网络参数

函数：saetrain.m ；nntrain.m

1, 循环for i = 1 :numel(sae.ae):

这里循环两次，第一次训练第一层的网络参数；第二次训练第二层的网络参数.

2, 每次循环进入nntrain函数

train_x=train_y，train_x是patches_1和patches_2按行连接后的图像，大小是181200*25。

for i = 1 :numepochs循环的次数是自己设置的，这里numepochs =3，在main函数中设置，意思是每层网络均训练三次。

     for i = 1 : numbatches,(numbatches=1812)，batch_x是从train_x中随机取100行，batch_x大小则是100*25，（这里循环1812次是因为每次训练都是任取100行数据，所以需要循环1812次，才能将所有输入训练完，这样做的原因是：比一次全部输入181200行元素能够大大降低权重W的参数数量，降低内存消耗，加快执行时间。）对batch_x添加噪声（标志位是nn.inputZeroMaskedFraction ~= 0）这里batch_x添加的噪声方法是随机的将一部分元素置0，其余不变；batch_y是未加噪的batch_x。

每次训练同时训练100个像素训练的流程是：nnff——>nnbp——>nnapplygrads，训练完成后得到新权重W，然后再用新权重W训练下100个像素，直到所有像素训练完得到最终的权重W。

nntrain函数流程如下：

图3 nntrain函数流程

图3中的流程进行一遍，完成一次网络的训练。训练第一层网络需要循环三次图3流程，训练第二层网络和fine-tuning均需要循环三次图3流程。

训练第一层网络：

2.1 nnff函数：执行网络前馈

     nnff(nn, x, y)，nn是网络结构，x是batch_x（100*25,加了噪声），y是batch_y（100*25，未加噪声的原始输入）。

nnff是网络前馈，（第一次使用的权重W是网络结构初始化的权重W，后面使用的权重W是前一次网络训练得到的权重W）.

 

 

图4 第一层网络前馈

第一层网络训练的前馈如图5所示，对batch_x加一列全为1的bias记为nn.a{1}，nn.a{1}乘以权重nn.W{1}，再取sigmoid函数，加一列全1的bias记为nn.a{2}; nn.a{2}乘以权重nn.W{2}，再取sigmoid函数，加一列全1的bias记为nn.a{3}，即输出Z.

nn.e =batch_y- Z; nn.e是误差，误差是原始未加噪输入batch_y和训练后的输出Z的差，

误差函数：

 

目标函数是min 来更新权重，最优化方法是使用BP算法和梯度下降法来得到目标函数的最优解。

2.2 nnbp函数：使用BP算法反求权重变化量dW

中间变量d：

d{3} = - nn.e.* (nn.a{3} .* (1 - nn.a{3}));

d{2} = d{3} *nn.W{2} .* nn.a{2} .* (1 - nn.a{2})

根据中间变量d来更新权值变化量dW的公式：

nn.dW{1} = (d{2}(:,2:end)'* nn.a{1}) / size(d{2}, 1);  

nn.dW{2} = (d{3}'* nn.a{2}) / size(d{3}, 1);

2.3  nnapplygrads函数：通过梯度下降法来更新权重W

    dW = nn.learningRate * dW{i}; 其中learningRate学习率自己设置1

nn.vW{i} =nn.momentum*nn.vW{i} + dW; 其中momentum自己设置为0.5，nn.vW初始化全0，结构和nn.W一样

dW = nn.vW{i};

nn.W{i} =nn.W{i} - dW;

其中i取值为1和2，先更新W{1}在更新W{2}

到这里网络完成一次训练。

 

 

训练第二层网络：

2.1 nnff函数

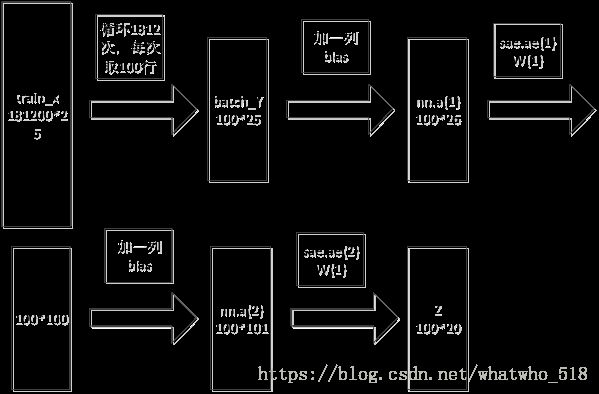
图5 第二层网络前馈

图4中的sae.ae{1}W{1}是第一层网络训练好后得到的权重，train_x乘以权重sae.ae{1}W{1}，得到第二层网络的原始输入，随机取100行得到batch_y，加噪声得到batch_x，对batch_x加一列全为1的bias记为nn.a{1}，nn.a{1}乘以权重nn.W{1}，再取sigmoid函数，加一列全1的bias记为nn.a{2}; nn.a{2}乘以权重nn.W{2}，再取sigmoid函数，加一列全1的bias记为nn.a{3}，即输出Z.

nn.e =batch_y- Z; nn.e是误差，误差是原始未加噪输入batch_y和训练后的输出Z的差，

误差函数：

2.2 nnbp函数

步骤同上

2.3 nnapplygrads函数

步骤同上

到这里网络完成一次训练。

3，saetrain.m函数执行完成后，完成pre-training的训练，新的权重W分别记为sae.ae{1}W{1}，sae.ae{1}W{2}，sae.ae{2}W{1} ，sae.ae{2}W{2}，

Fine-tuning

1，网络结构初始化

函数saesetup.m ；nnsetup.m;

Fine-tuning阶段是针对整个网络进行的微调，整个网络的结构为：

25——>100——>20——>100——>25，初始权重采用pre-training训练好的四个权重，25——>100的映射选择权重sae.ae{1}W{1}，100——>20的映射选择权重sae.ae{2}W{1}，20——>100的映射选择权重sae.ae{2}W{2}，100——>25的映射选择权重sae.ae{1}W{2}。

2，训练网络参数

函数：saetrain.m ；nntrain.m

具体流程使用的函数和pre-training相同。

2.1 nnff函数

图6 Fine-tuning前馈

           前馈网络如图5所示，train_x是patches_1和patches_2按行连接后的图像，大小是181200*25，然后任取100行记为batch_y，对batch_y加噪声记为batch_x(加噪声的方式是将部分元素置0)，对batch_x加一列全为1的bias记为nn.a{1}，nn.a{1}乘以权重nn.W{1}（nn.W{1}等于前面训练好的sae.ae{1}W{1}），再取sigmoid函数，加一列全1的bias记为nn.a{2};nn.a{2}乘以权重nn.W{2}（nn.W{2}等于前面训练好的sae.ae{2}W{1}），再取sigmoid函数，加一列全1的bias记为nn.a{3}; nn.a{3}乘以权重nn.W{3}（nn.W{3}等于前面训练好的sae.ae{2}W{2}），再取sigmoid函数，加一列全1的bias记为nn.a{4}; nn.a{4}乘以权重nn.W{4}（nn.W{4}等于前面训练好的sae.ae{1}W{2}），再取sigmoid函数记为nn.a{5}; 网络的最后输出Z就是nn.a{5}。

误差函数：

 

通过min 来得到新的权重。

2.2 nnbp函数

步骤同上

2.3 nnapplygrads函数

步骤同上

到这里网络完成一次训练。

3，saetrain.m函数执行完成后，完成fine-tuning的训练，新的权重W分别记为sae.ae{1}W{1}，sae.ae{1}W{2}，sae.ae{2}W{1} ，sae.ae{2}W{2}，

三、SDAE提取特征

经过上面的pre-training和fine-tuning后，网络就训练好了，然后重新将train_x输入网络，就得到了20维特征。最终的Z就是输出的10维特征。

图7 SDAE提取特征