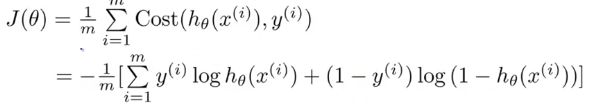Machine Learning Wu Enda4
chapter 42 Classification
classification problems where the variable y that you want to predict is a discrete value.
Email:Spam?
Online : transactions: Fraudulent?
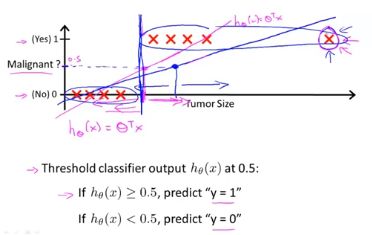
Tumor:Malignant benign?
y∈0,1 y ∈ 0 , 1 0:”Negative Class” (e.g. benign tumor) 1:”Positive Class”(e.g. malignant tumor)
Classification : y = 0 or 1
hθ(x) h θ ( x ) can be >1 or <0
Logistic Regression : 0<=hθ(x)<=1 0 <= h θ ( x ) <= 1
chapter 43 Hypothesis Representation
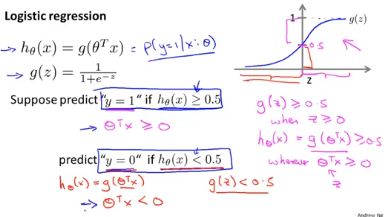
Want 0<=hθ(x)<=1 0 <= h θ ( x ) <= 1
hθ(x)=g(θTx) h θ ( x ) = g ( θ T x )
g(z)=11+e−z g ( z ) = 1 1 + e − z -> Sigmoid function Logistic function

Interpretation of Hypothesis Output:
chapter 44 Decision boundary
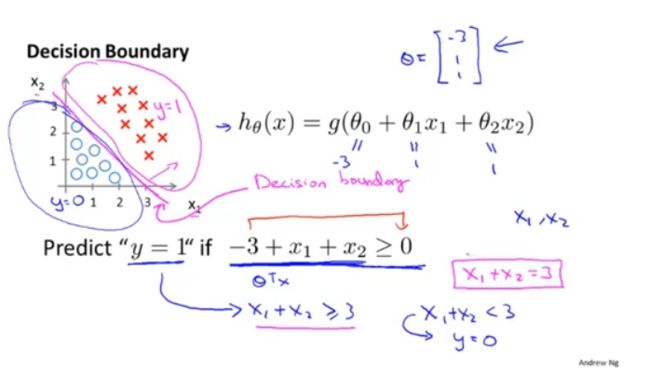
decision boundary:
the magenta line is called the decision boundary.
Non-linear decision boundaries:
decision boundary is a property not of the training set ,but of the hypothesis and of the parameters
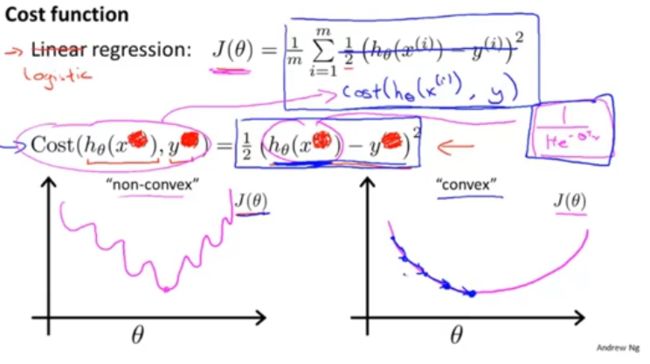
chapter 45 Cost function
non linear sigmoid function . J(θ) J ( θ ) ends up being a non convnex function if you were to define it as the squared cost function .
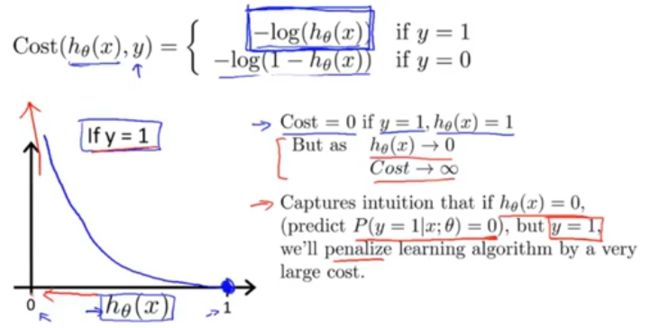
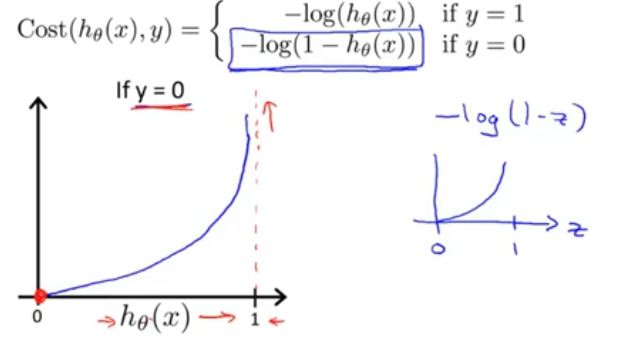
Logistic regression cost function:
if y = 1 :
if y = 0:
chapter 46 Simplified cost function and gradient descent
Logistic regression cost function:
this cost function can be derived from statistics using the principle of maximum likelihood estimation,which is an idea statistics for how to efficiently find parameters data for different models.And it also has a nice property that it is convex.
chapter 47 Advanced optimization
advanced optimization algorithms and some advanced optimization concepts.
Optimization algorithm:
Give θ θ ,we have code that can compute:
Optimization algorithms:
- Gradient descent
- Conjugate gradient
- BFGS
- L-BFGS
Advantages:
- No need to manually pick a a .
- Often faster than gradient descent.
Disadvantages:
- More complex
E.g:
simple quadratic cost function:
chapter 48 Multi-class classification : One-vs-all
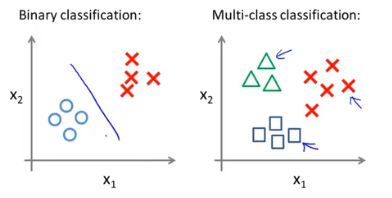
Multi-class classification :
Email foldering /tagging:Work Friends family hobby
Medical diagrams Not ill Clod Flu
Weather :Sunny rain Snow
One-vs-all:
Train a logistic regression classifier h(i)θ(x) h θ ( i ) ( x ) for each class i to predict the probability that y = i .
On a new input x x , to make prediction ,pick the class i i that maximizes.
maxi h(i)θ(x) m a x i h θ ( i ) ( x )