算法设计与分析:动态规划(3)-序列联配问题(以算代存)
文章目录
- 前言
- 高级动态规划
- 应用分治思想减少空间
- 计算得分
- 从后缀匹配到前缀匹配
- 伪代码
- 分治点计算改进
- 总结
本文参考UCAS卜东波老师算法设计与分析课程撰写
前言
本文内容承接上一次算法设计与分析:动态规划(2) - 序列联配问题(最优对齐方案),讲述高级动态规划的内容。
在前文,我们已经解决了求序列联配中最优对齐的问题。但是完成的方案仍有缺陷:内存消耗过大。对于两个字符串 S m S_m Sm, T n T_n Tn,我们计算其最优对齐,需要的数组空间是 O ( m n ) O(mn) O(mn),这在上面的例子中看不出来,但是如果给我们的不是一个短字符串,而是两篇存储量几十KB的文章,让我们做对齐,可想而知,总的内存占用就是几百MB,如果单个内存更大呢?另一方面,时间上由于算法采用两层for循环计算整个二维数组,但最后我们很可能用不到那些多余的内容(数组的边角部分),这就浪费了很多计算时间。显然,这种解决方案就不适用了。
高级动态规划
动态规划对于最优解的获取有着十分显著的效果,但唯一让人诟病的就是其占用大量的存储空间和许多不必要的计算。而高级动态规划弥补了这一缺陷,其节省了存储空间和运行时间。采用方法是以算代存。
应用分治思想减少空间
计算得分
首先思考一个问题,我们每次计算当前格子的分值,考虑的是其左上角三个格子的内容,其余格子都不做考虑,实际上我们每次计算并不需要完整的二维数组的所有数据,只需下如下两列的数据即可:
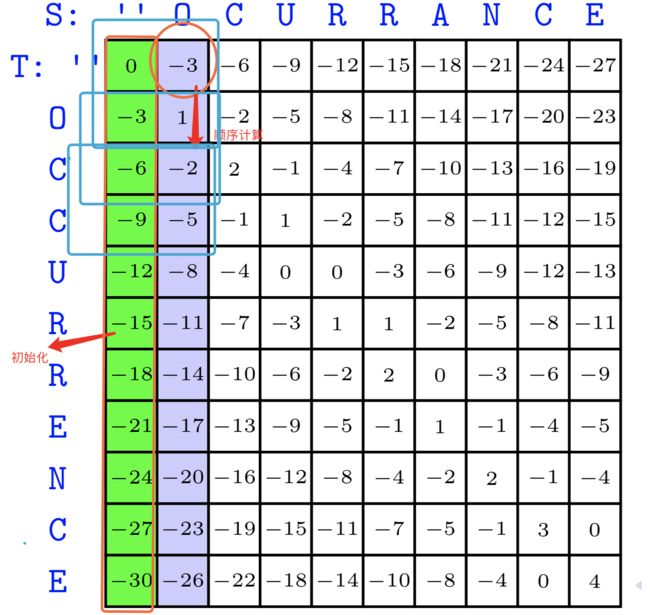
一开始,我们初始化第0列(耗费一个数组),当计算第1列的时候,第一个元素-3可以直接初始化得到,对于第一个蓝色框框,左上角三个值都已得到,直接根据递推表达式,得到1,在此基础上进行第二个蓝色框框的计算,以此类推,计算得到前2列的内容
而在计算第2列的内容时,第0列的内容我们已经没必要保存了,因此将第1列的数值保存到前一个数组中,进行下一轮的计算,如下图:
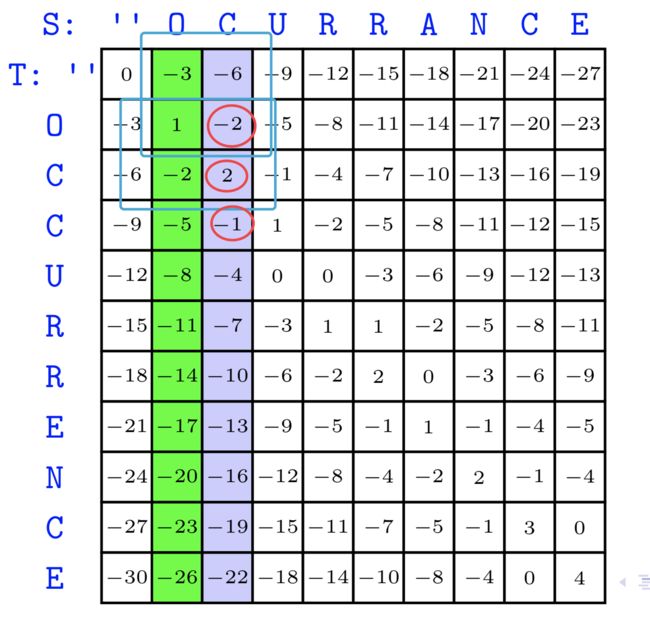
最终我们数组保存的内容只有最后两列,自然就得到了最后的答案4. 我们容易得到该伪代码如下:

上面这个方法也告诉我们,如果只关心最优的分值,只需要O(2n)的空间复杂度即可,n是T的长度
-
回溯得到路径
上面的方法在计算最终得分上没有问题,但是出现了一个问题,由于最后我们只保存了最后两列,回溯的时候到3,就会发现回溯不动了,因为我们找不到往前的数据了。Hirschberg的算法解决了这一问题,它将分治思想应用到了动态规划当中。我们依然从多步决策的角度思考,S如何从T一步步产生?应用分治的思想,我们将S分成两部分,前半部分从T的前一部分产生,后半部分从T的后一部分产生,得到公式如下:
O P T ( T , S ) = O P T ( T [ 1.. q ] , S [ 1.. n 2 ] ) + O P T ( T [ q + 1.. m ] , S [ n 2 + 1.. n ] ) OPT(T,S) = OPT(T[1..q],S[1..\frac{n}{2}])+OPT(T[q+1..m],S[\frac{n}{2}+1..n]) OPT(T,S)=OPT(T[1..q],S[1..2n])+OPT(T[q+1..m],S[2n+1..n])这个公式将S一分为二,它认为S的前半截是从T[1…q]产生的,后半截是T[q+1…m]产生的,q是一个未知量。注意,此式成立的前提是打分是线性加和的。
从后缀匹配到前缀匹配
这里我们需要先了解一个信息,之前我们对S,T动态规划计算是从后往前的,实际上我们从前往后对比计算也是可以的,只不过是把原公式中-1(坐标前移)的操作换成+1(坐标后移)即可。下面是采用前缀匹配得到结果的例子:
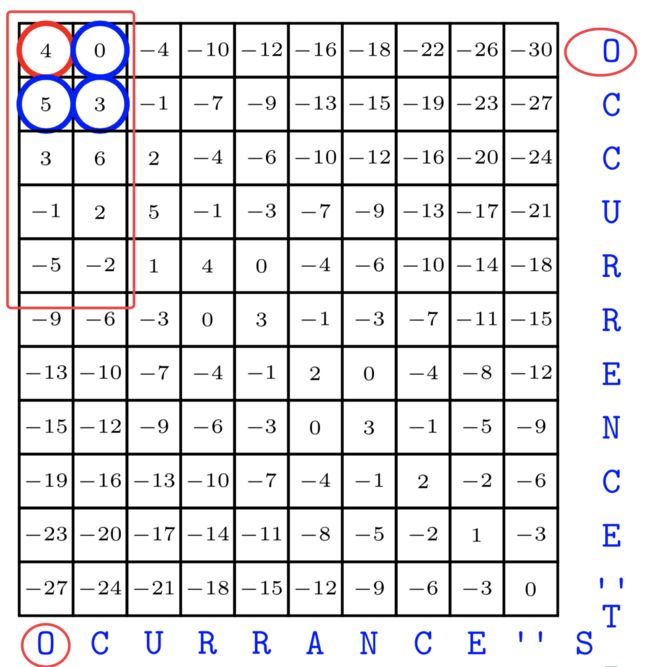
可以看到先对“O”进行递归查询,这部分的内容与上一篇类似,不多赘述,有遗忘的可以回去翻看一下上一篇的推导。、
前面我们应用了分治思想,将S分成两部分,那么我们就可以分别对前半部分采用后缀匹配,后半部分采用前缀匹配,并且只用两个数组存储中间结果,如下:
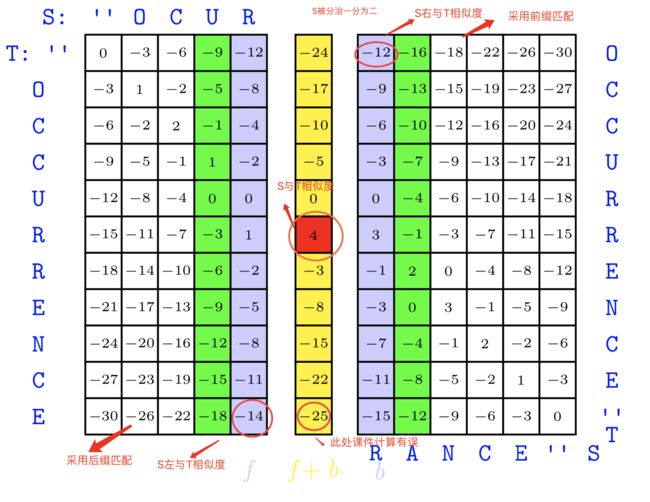
注意图中灰色部分的结果,它们是匹配过后的得分结果,也就是“OCUR”和“OCCURRENCE”最终最优匹配分值是-14,“RANCE”和“OCCURRENCE”最终最优匹配分值是-12。我们将这两列的结果加起来,得到中间黄色列的结果,发现中间得到了之前计算的最优分值4!它是由1+3得到的。1是“OCUR”和“OCCUR“相似度,3是”RANCE“和”RENCE“相似度,由于我们采用线性加和得分,1+3的结果就是S与T的相似度!等一下,那这个4出现的位置有什么意义呢?看下面这张图:
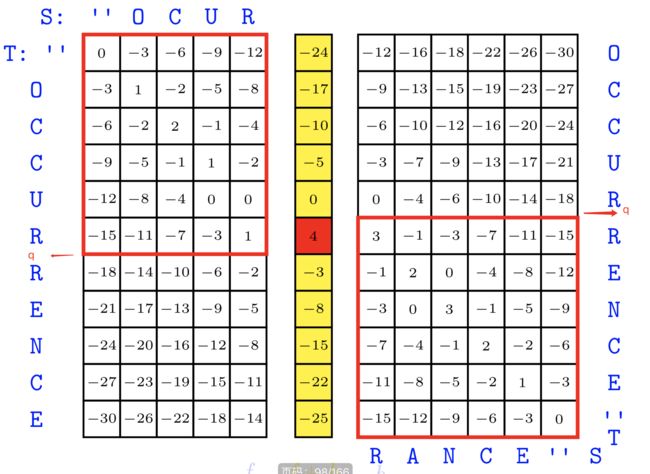
我们发现4将左右分成了上下两部分,而这里的R正好就是q的位置。我们由此可以得到原公式第一次分治如下:
O P T ( ′ O C C U R R E N C E ′ , ′ O C U R R A N C E ′ ) = O P T ( ′ O C C U R ′ , ′ O C U R ′ ) + O P T ( ′ R E N C E ′ , ′ R A N C E ′ ) OPT('OCCURRENCE','OCURRANCE') = OPT('OCCUR','OCUR') +\\ OPT('RENCE','RANCE') OPT(′OCCURRENCE′,′OCURRANCE′)=OPT(′OCCUR′,′OCUR′)+OPT(′RENCE′,′RANCE′)
剩下的就是对左上角红色区域和右下角红色区域进行递归调用,我们就可以得到一系列像之前4一样的红色格子。
那么,该如何得到想要的路径呢?要想到路径,首先要真正理解q的意义,q表明了S的前一半是从T的[1…q]得到的,体现在例子中,就是"OCUR"是从“OCCUR”来的,这个我们肉眼就能轻易看出,符合事实。回到之前的路径表上:
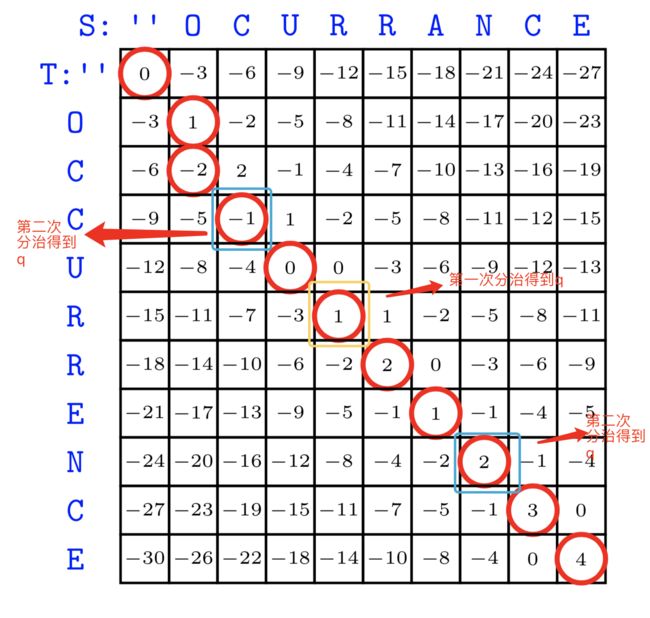
我们从图中容易知道,每一个行至少有一个元素在路径中,而q确定了这个元素所处的列!第一次分治的q确定了中间黄色的1的位置,q的值是5,也即告诉我们原二维数组<5,4>一定在路径中,4是一开始S一分为二确定的。同样的,每次递归我们都能确定新的在路径中的元素。这样我们就可以慢慢确定路径了。
伪代码
上面的算法十分巧妙地运用了分治思想,我们只需要开f,b两个数组O(m)的空间和A数组O(n)的空间,所以总的空间耗费是O(m+n),为线性存储空间。
这个算法的时间复杂度也是O(mn)的,证明过程较为繁琐不做赘述。
分治点计算改进
上面的算法固然很好,但也存在缺点,我们关注伪代码的2,3两行,这里要求问题必须可以从前往后计算,也能从后往前计算,在对齐问题中可以这么做,但如果放到其他不能两头皆可的问题就显得无力了。
要获得路径,根据上文的推导,实际上只要将q递归地计算出来即可,定义一个变量 R i , j R_{i,j} Ri,j表示单元(i,j)回溯到(0,0)在哪一行经过 n 2 \frac{n}{2} 2n,我们有如下公式:
R i , j = { i if j = ⌊ n 2 ⌋ R i − 1 , j if j > ⌊ n 2 ⌋ a n d O P T [ i , j ] = O P T [ i − 1 , j ] + s ( T i , ′ − ′ ) R i − 1 , j − 1 if j > ⌊ n 2 ⌋ a n d O P T [ i , j ] = O P T [ i − 1 , j − 1 ] + s ( T i , S j ) R i , j − 1 + if j > ⌊ n 2 ⌋ a n d O P T [ i , j ] = O P T [ i , j − 1 ] + s ( ′ − ′ , S j ) R_{i,j}= \begin{cases} i &\text{if } j = \lfloor \frac{n}{2} \rfloor \\ R_{i-1,j} &\text{if } j> \lfloor \frac{n}{2} \rfloor \ and \ OPT[i,j] = OPT[i-1,j]+s(T_i,'-') \\ R_{i-1,j-1} &\text{if } j> \lfloor \frac{n}{2} \rfloor \ and \ OPT[i,j] = OPT[i-1,j-1] + s(T_i,S_j) \\ R_{i,j-1}+ &\text{if } j> \lfloor \frac{n}{2} \rfloor \ and \ OPT[i,j] = OPT[i,j-1]+ s('-',S_j) \\ \end{cases} Ri,j=⎩⎪⎪⎪⎨⎪⎪⎪⎧iRi−1,jRi−1,j−1Ri,j−1+if j=⌊2n⌋if j>⌊2n⌋ and OPT[i,j]=OPT[i−1,j]+s(Ti,′−′)if j>⌊2n⌋ and OPT[i,j]=OPT[i−1,j−1]+s(Ti,Sj)if j>⌊2n⌋ and OPT[i,j]=OPT[i,j−1]+s(′−′,Sj)
此处我与课件上内容不太一样,个人认为这里是课件有误,缺少了一个分值的变化
先不急着理解公式,我们看一个例子就明白:
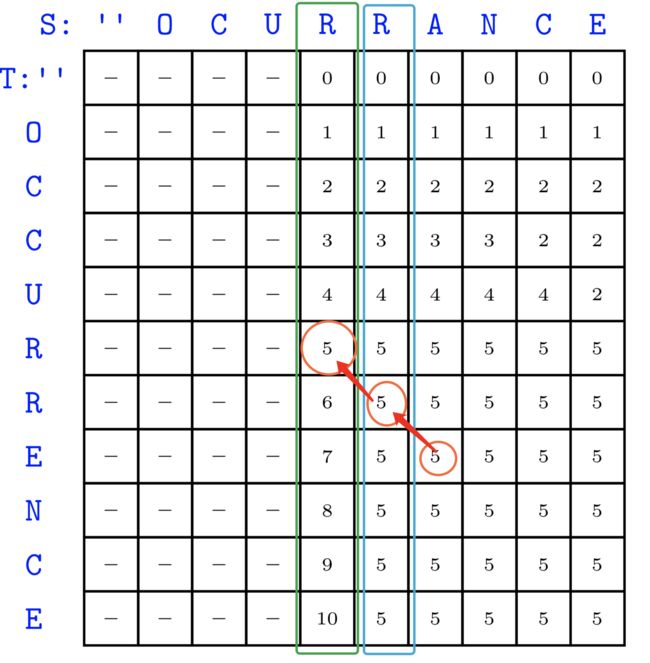
首先,对于刚好在 n 2 \frac{n}{2} 2n列的元素,其通过 n 2 \frac{n}{2} 2n列时的行必然是其本身行,而对于后面列的元素,我们就需要考虑其OPT的计算结果了。为了方便对照,贴一下两者对比图:

我们知道,在递归计算的时候,我们总是有两个数组(一绿,一蓝)用于保存当前计算的最优对齐,对于 n 2 + 1 \frac{n}{2}+1 2n+1列的元素,它想知道自己回溯的时候在哪一行通过 n 2 \frac{n}{2} 2n列,它需要向前询问。询问的基础在于它是从哪里走过来的,根据OPT的分值对比,我们可以清楚知道蓝色框中的5是从绿色框中的5得来的,同样我们不断向后更新,可以得到最后一列结果为5,这说明了 q = R 10 , 9 = 5 q=R_{10,9}=5 q=R10,9=5 ,我们用这个方法实现了q的查找,剩下就是递归的过程了。下面是递归计算的一个例子:

可以递归调用是计算“OCUR”,“OCCUR”之间的q,当计算“OC”,“OCC”的时候q的值有两个,这也很好理解,“O-C”可以与“OCC”对齐,“OC-”也可以与“OCC”对齐,因此q有两个选项。
下面是整个递归过程存储的路径点过程(图片来源课件):

那么我们就有路径点集 A = { ⟨ 5 , 4 ⟩ , ⟨ 3 , 2 ⟩ , ⟨ 1 , 1 ⟩ , ⟨ 4 , 3 ⟩ , ⟨ 7 , 6 ⟩ , ⟨ 6 , 5 ⟩ , ⟨ 8 , 7 ⟩ , ⟨ 9 , 8 ⟩ } A=\{\lang 5, 4\rang, \lang3, 2 \rang, \lang 1, 1\rang, \lang 4,3\rang, \lang 7,6\rang, \lang6,5\rang, \lang8,7\rang, \lang9,8\rang\} A={⟨5,4⟩,⟨3,2⟩,⟨1,1⟩,⟨4,3⟩,⟨7,6⟩,⟨6,5⟩,⟨8,7⟩,⟨9,8⟩}
这个过程一定要自己动手画一画,能有更清楚的认识,实际上它的动态过程和求OPT的时候类似,先初始化第一绿色列(这里的初始化是 R i , j R_{i,j} Ri,j就是行号),然后蓝色列根据绿色列和递推式计算得到,蓝色列后面的又根据蓝色列得到,依此递推,最终得到最后一列。
总结
本文在前文序列联配问题的动态规划基础上,实现了空间复杂度的降低。开头给出了计算最优分值的方法,只需两个数组存储。但是这种方法没办法回溯得到路径,从而打印对齐的字符串。因此提出了Hirschberg的算法,在动态规划中应用分治思想,其能够降低空间复杂度的核心是以算代存,其大致步骤如下:
- 将原本S如何从T中产生的多步决策问题,转换成了S的前一半如何从T的前一部分产生( T [ 1.. q ] , S [ 1.. n 2 ] T[1..q],S[1..\frac{n}{2}] T[1..q],S[1..2n])+S的后一半如何从T的后一部分产生( T [ q + 1.. m ] , S [ n 2 + 1.. n ] T[q+1..m],S[\frac{n}{2}+1..n] T[q+1..m],S[2n+1..n])
- 接下来我们对前后两部分分别采用后缀最优对齐,前缀最优对齐,最后计算得到两列结果,将两列结果求和,取最大者(就是之前的4)的横坐标就是q
- 有了q,我们就能存储 ⟨ q , n 2 ⟩ \lang q,\frac{n}{2} \rang ⟨q,2n⟩(路径必经之点)到数组中,然后递归1-2步过程,最终得到的数组A构成了我们需要的路径
但上述方法有一定限制,它要求问题必须同时满足前缀最优对齐和后缀最优对齐,因此我们又提出了lan的算法,本质上我们要找到路径就是找到q这个值,因此他考虑利用OPT递归计算q,同样得到点集A。
这篇文章涵盖的内容要比之前更难,但其实用性也更高,能够帮助我们节省大量动态规划中消耗的内存。因此,建议一定要好好理解消化,受益匪浅。
如果你觉得文章对你有用,不妨顺手点个赞哦~
- 上一篇:算法设计与分析:动态规划(2) - 序列联配问题(最优对齐方案)
- 下一篇:算法设计与分析:动态规划(4)- 序列联配问题(观察回溯路径)
- 目录
