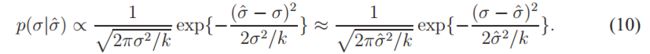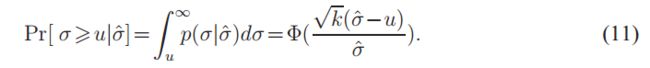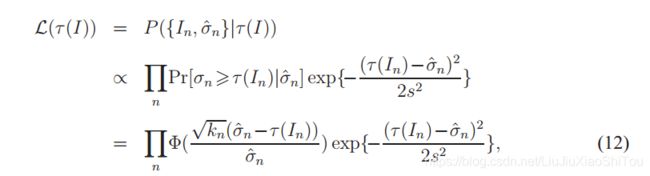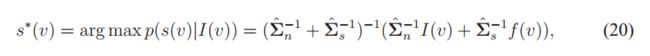《Automatic Estimation and Removal of Noise from a Single Image》阅读笔记
(06年的文章,原以为还是深度的,好吧,,,就硬着头皮看了一下,希望可以学到一些东西,学到一些传统的东西,好像并没有什么用。。。。。)
自动估计和消除单个图像中的噪声
图像降噪算法通常假定与实际RGB值无关的加性高斯白噪声(AWGN)处理。 这种方法不是完全自动的,不能有效消除当今CCD数码相机产生的色噪。 在本文中,我们为两个任务提出了一个统一的框架:使用分段平滑图像模型自动估计和消除单个图像中的颜色噪声。 我们介绍了噪声水平函数(NLF),这是一个连续函数,将噪声水平描述为图像亮度的函数。 然后,我们通过将下包络拟合每个段图像方差的标准偏差来估计实际噪声水平函数的上限。 对于降噪,通过将像素值投影到适合每个段中RGB值的线上,可以显着消除色彩噪声的色度。 然后,构造高斯条件随机场(GCRF),以从嘈杂的输入中获得底层的干净图像。 进行了广泛的实验以测试所提出的算法,该算法的性能优于最新的去噪算法。
关键词:图像去噪 分段光滑图像模型 基于分割的计算机视觉算法 噪声估计 高斯条件随机场 自动视觉系统
1. 介绍
图像降噪已经在计算机视觉,图像处理和统计信号处理中研究了数十年。 这个问题不仅为检查自然图像模型和信号分离算法提供了一个良好的平台,而且成为数字图像获取系统中提高图像质量的重要组成部分。 这两个方向都很重要,将在本文中进行探讨。
现有的大多数图像去噪工作都是假设加性高斯白噪声(AWGN)并消除与RGB通道无关的噪声。 但是,如果相机的系列和品牌以及相机设置(ISO,快门速度,光圈和闪光灯开/关)未知,则数码相机产生的噪音的类型和级别是未知的。 例如,每张图片附带的可交换图像文件格式(EXIF)元数据可能会在图像格式转换和图像文件传输中丢失。 同时,由于嵌入在相机中的去马赛克处理,颜色噪声的统计信息并不独立于RGB通道。 因此,当前的去噪方法不是真正的自动方法,并且不能有效地消除颜色噪声。 该事实阻止了噪声去除技术被实际应用于数字图像降噪和增强应用。
在某些图像去噪软件中,要求用户指定多个平滑图像区域以估计噪声水平。 这促使我们采用基于分段的方法来自动估计单个图像的噪声水平。 由于噪声水平取决于图像亮度,因此我们建议从图像估计噪声水平函数(NLF)的上限。 图像被分为多个分段平滑区域,其中平均值是亮度的估计,而标准偏差是噪声水平的高估。 噪声级功能的先验是通过模拟数码相机的成像过程来学习的,并用于在丢失数据的情况下帮助正确估计曲线。
由于从单个输入中分离信号和噪声受到了限制,因此从理论上讲不可能从受噪声污染的观察中完全恢复原始图像。图像去噪的目的是在消除噪声的同时尽可能保留图像特征。 在设计图像去噪算法时,我们需要匹配许多原理。
(a)感知上平坦的区域应尽可能平滑。 这些区域应完全消除噪音。
(b)图像边界应妥善保存。 这意味着不应模糊或锐化边界。
(c)纹理细节不应丢失。 这是最难匹配的条件之一。 由于图像去噪算法倾向于平滑图像,因此平滑过程中很容易丢失纹理节。
(d)应保留全局对比度(即,去噪后的低频图像和输入图像应相同)。
(e)去噪图像中不应出现伪像。
全局对比度可能是最容易匹配的,而其他一些原理几乎是不兼容的。 例如,(a)和(c)很难一起调整,因为大多数降噪算法无法从单个输入图像中区分出平坦区域和纹理区域。 另外,满足(e)也很重要。 例如,基于小波的去噪算法倾向于产生振铃伪像。
理想情况下,应将同一图像模型用于噪声估计和降噪。 我们发现基于细分的方法同样适用于这两项任务。 在将自然图像过度分割成分段平滑区域后,由于图像形成的物理定律,每个段内的像素值大约位于RGB空间中的1D线上[25,23,19]。这个重要的事实有助于显着降低色彩噪声。 我们通过构造高斯条件随机场(GCRF)来从噪声图像中估算出干净图像(信号)来改善结果。
进行了实验,结果令人信服,并且在视觉上令人愉悦,以证明我们基于分段的降噪算法优于现有技术。 由于噪声水平是自动估计的,因此我们的方法具有明显的自动性。自动估计噪声水平也可以使其他计算机视觉算法受益。 例如,可以将立体声,运动估计,边缘检测和超分辨率算法的参数设置为噪声水平的函数,这样我们就可以避免针对不同噪声水平调整参数。
本文的结构如下。 在回顾了第2节中的相关工作之后,我们在第3节中介绍了我们的分段平滑图像模型。在第4节中,我们提出了从单个图像进行噪声估计的方法。 我们在第5节中详细介绍了基于分割的图像去噪算法,第6节中显示了结果。第7节中讨论了色彩噪声,建模和自动化问题,第8节中提供了总结。
2. 相关工作
在本节中,我们将简要回顾以前在图像降噪和噪声估计方面的工作。 图像去噪技术在图像先验模型的选择上有所不同,而现有的噪声估计技术则假定加性高斯白噪声(AWGN)。
2.1 图像去噪
在过去的三十年中,在图像处理和计算机视觉社区中已经开发了多种去噪方法。 尽管看似非常不同,但是它们都具有相同的属性:保留有意义的边缘并删除不太有意义的边缘。 我们通过不同的自然图像先验模型和自然图像统计的相应表示对现有图像去噪工作进行分类。
小波:当自然图像分解为面向多尺度的子带[30]时,我们观察到峰度边缘分布[15]。 为了强制边缘分布具有高峰度,我们可以简单地抑制低振幅值,同时保留高振幅值,这是一种称为取心的技术[39,43]。
在[42]中,发现小波的联合分布是相关的。 开发了一种联合取芯技术,以在不同方向和比例子带上同时推断小邻域中的小波系数。 去噪的典型联合分布是高斯比例混合(GSM)模型[37]。 另外,小波域隐马尔可夫模型已经被应用到图像去噪中,并获得了有希望的结果[8,13]。
尽管基于小波的方法在去噪中很流行并且占主导地位,但是很难去除小波重构的振铃伪影。 换句话说,基于小波的方法倾向于在去噪图像中引入其他边缘或结构。
各向异性扩散:最简单的噪声消除方法是高斯滤波,它等效于求解各向同性的热扩散方程[46],即二阶线性PDE。 为了保持锋利的边缘,可以使用 [34]进行各向异性扩散,其中
[34]进行各向异性扩散,其中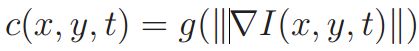 ,而g是单调递减函数。 结果,对于高梯度像素,
,而g是单调递减函数。 结果,对于高梯度像素,![]() 小,因此扩散较少。 对于低梯度像素,
小,因此扩散较少。 对于低梯度像素,![]() 具有较高的值,并且这些像素被相邻像素模糊。 在[3]中讨论了选择g(·)的更复杂的方法。 与简单的高斯滤波相比,各向异性扩散可以在保持边缘的同时消除噪声。但是,它倾向于使图像过度模糊并锐化边界,并丢失许多纹理细节。
具有较高的值,并且这些像素被相邻像素模糊。 在[3]中讨论了选择g(·)的更复杂的方法。 与简单的高斯滤波相比,各向异性扩散可以在保持边缘的同时消除噪声。但是,它倾向于使图像过度模糊并锐化边界,并丢失许多纹理细节。
已经开发了更高级的偏微分方程(PDE),以便为给定的(用户定义的)基础局部平滑几何设计一个特定的正则化过程[52],比经典的各向异性扩散方法保留更多的纹理细节。
框架和FOE: 作为测量小波系数上的边际或联合分布的一种替代方法,可以从边际分布中学习整个图像的完整先验模型[18,55]。 因此,自然可以使用贝叶斯推理进行降噪或恢复[54,40],其形式为: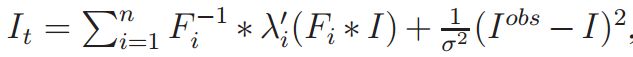 ,其中
,其中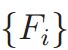 是线性滤波器(
是线性滤波器( 是通过将
是通过将![]() 镜像到其中心像素周围而获得的滤波器),
镜像到其中心像素周围而获得的滤波器),![]() 是对应的吉布斯势函数,σ2是噪声的方差,t是迭代指数。因为导数
是对应的吉布斯势函数,σ2是噪声的方差,t是迭代指数。因为导数![]() 通常具有接近零的高值和高振幅的低值,所以如果将Fi视为不同方向的导数滤波器,则上述PDE非常类似于各向异性扩散[54]。
通常具有接近零的高值和高振幅的低值,所以如果将Fi视为不同方向的导数滤波器,则上述PDE非常类似于各向异性扩散[54]。
使用MCMC学习Gibbs分布可能效率不高。 同时,这些方法具有与各向异性扩散相同的缺点:过度平滑和边缘锐化。
双边过滤:适应高斯滤波以保留边缘的另一种方法是双边滤波[51],其中同时考虑了空间距离和距离距离。 文献[2]推导了双边滤波与各向异性扩散之间的本质关系。 在[10,33]中也提出了快速双边滤波算法。
双边滤波已被广泛认为是一种简单有效的降噪算法,尤其是在恢复HDR图像时对彩色图像进行降噪[10]。 但是,它不能处理斑点噪声,并且也具有过度平滑和边缘锐化的趋势。
非局部方法:如果场景和摄像机都是静态的,我们可以简单地拍摄多张照片并使用均值消除噪点。 该方法对单个图像不切实际,但是可以从空间均值中计算出时间均值-只要单个图像中有足够的相似图案即可。 我们可以找到与查询补丁相似的模式,并采用均值或其他统计信息来估算真实像素值,例如,在[1,5]中。 这种方法的更严格的表述是通过对噪声输入的稀疏编码[11]。
对于包含许多重复图案的类似纹理的图像,非局部方法效果很好。与具有![]() 复杂度(其中n是图像宽度)的其他降噪算法相比,这些算法具有
复杂度(其中n是图像宽度)的其他降噪算法相比,这些算法具有![]() 时间复杂度,这对于现实世界的应用是禁止的。
时间复杂度,这对于现实世界的应用是禁止的。
条件随机场: 最近,条件随机场(CRF)[26]已经成为一种有前途的统计推断模型。 由于没有明确的信号先验模型,CRF可以灵活地对短距离和远距离约束及统计数据进行建模。 由于嘈杂的输入和干净的图像在图像特征处对齐良好,因此CRF(尤其是高斯条件随机场(GCRF))可以很好地应用于图像去噪。 在[47]的去噪工作中已经显示出初步的成功。 在[49]中也讨论了学习GCRF。
2.2 噪声估计
可以从多个或单个图像中估计与图像有关的噪声。 从多个图像进行估计是一个过度约束的问题,在[24]中已解决。 但是,从单个图像进行估计是一个约束不足的问题,因此必须对噪声进行进一步的假设。 在图像去噪文献中,噪声通常被认为是加性高斯白噪声(AWGN)。 广泛使用的估计方法是基于平均绝对偏差[9]。 在[16]中,从平滑或小的纹理区域的梯度估计噪声水平,并针对每个强度间隔估计与信号相关的噪声水平。 在[45]中,作者提出了三种基于训练样本和自然图像的统计量(拉普拉斯)估计噪声水平的方法。 在[36]中,提出了一种广义期望最大化算法来估计破坏观测图像的噪声源的频谱特征。
已经提出了用于噪声估计然后降低噪声的技术,但是它们倾向于启发式。 例如,在[21]中,使用一组胶片颗粒噪声统计数据来估计和消除在均匀曝光下扫描照相元件产生的噪声。 在[44]中,通过用自适应阈值分割图像梯度,从图像的平滑区域估计与信号有关的噪声。 估计的信号相关噪声会应用于整个图像,以降低噪声。 在[20]中,这项工作得到了进一步的扩展,它基于图像的源识别标签将默认的与电影相关的噪声模型与图像相关联。 然后使用图像统计信息调整噪声模型。 在某些市售的图像增强软件(例如Neat ImageTM1)中,可以通过指定无特征区域来剖析噪声来半自动估计噪声水平。Neat ImageTM还提供校准工具来估计特定相机和相机设置的噪点数量; 还可以使用各种摄像机的预先校准的噪声曲线来直接对图像进行降噪。
相比之下,我们的技术避免了使用的每个摄像机的繁琐的噪声测量过程。 此外,我们的技术为在贝叶斯推断框架下从单个图像估计连续噪声水平函数提供了一种原理方法。
3 分段平滑图像模型
Terzopoulos [50]首先将分段平滑图像模型引入计算机视觉文献,以说明重建图像的正则化。 布莱克和齐瑟曼[4]详细阐述了分段平滑(或连续)的概念。 在本节中,我们将从图像中重建分段平滑图像模型以及该模型的一些重要属性。
3.1 图像分割
在将像素划分为具有相似空间坐标和RGB像素值的区域之前,基于分段平滑图像设计图像分割算法。 有多种分割算法,例如均值偏移[7]和基于图的方法[14]。由于本文的重点不在分割上,因此我们选择一种K-means聚类方法将像素分组为区域,如[56]中所述。 每个部分由平均颜色和空间范围表示。 计算空间范围,以使片段的形状偏向凸形,并且所有片段的大小相似。
3.2 分割统计和仿射重建
令图像晶格为![]() 。它被完全划分为多个区域{Ωi},其中
。它被完全划分为多个区域{Ωi},其中![]() 。 设
。 设![]() 为坐标变量,而I
为坐标变量,而I![]() 为像素的RGB值。 由于在本节中,我们专注于每个分段内的统计信息,因此我们将使用Ω表示一个分段,使用v∈Ω索引分段Ω中的像素。
为像素的RGB值。 由于在本节中,我们专注于每个分段内的统计信息,因此我们将使用Ω表示一个分段,使用v∈Ω索引分段Ω中的像素。
我们可以将仿射模型拟合到段Ω中以最小化平方误差
我们假设残差由两部分组成:细微的纹理变化h(v)(也是信号的一部分)和噪声n(v),即r(v)= h(v)+ n(v)。 换句话说,观察到的图像可以分解为I(v)= f(v)+ h(v)+ n(v)。 因此,基本的干净图像或信号为s(v)= f(v)+ h(v),这将根据噪声输入进行估算。 s(v),h(v),n(v)是RGB空间中的所有3D向量。
令I(v),s(v),h(v)和n(v)的协方差矩阵分别为ΣI,Σs,Σh和Σn。 我们假设f(v)是一个非随机过程,而r(v)和n(v)是随机变量。因此,∑s = ∑h。 假设信号s(v)和噪声n(v)是独立的,
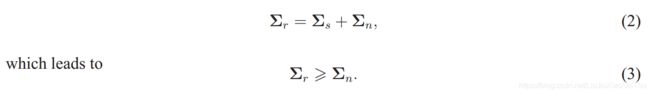 3.3 边界模糊估计
3.3 边界模糊估计
如果仅使用每段仿射重建,则重建的图像具有人为边界,原始边界会变得清晰。 因此从原始图像估计模糊量。 对于从![]() 的每个假设模糊b,以Δb(= 0.25)为步长,我们计算模糊图像
的每个假设模糊b,以Δb(= 0.25)为步长,我们计算模糊图像![]() 其中G(u; b)是具有sigma b的高斯核。 然后我们计算误差图像Ierr,以使
其中G(u; b)是具有sigma b的高斯核。 然后我们计算误差图像Ierr,以使
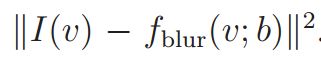 。 我们将每个边界曲线Cij扩展五次到Ωi和Ωj中,以获得蒙版ijij。 Cij的最佳模糊b * ij对应于Γij上的最小集合误差
。 我们将每个边界曲线Cij扩展五次到Ωi和Ωj中,以获得蒙版ijij。 Cij的最佳模糊b * ij对应于Γij上的最小集合误差![]()
为了恢复过渡区域Γij中的模糊,我们只需将f(v)替换为fblur(v; b ∗ i j)。请注意,这是假设Ωi和Ωj的模糊量相同,通常严格来讲这是不正确的。 但是,我们发现这种近似可以产生足够好的结果。对每个区域完成此过程后,我们获得边界模糊的分段仿射重构fblur(v)。
分段平滑图像模型如图1所示。通过分割算法,将从Berkeley图像分割数据库[31]中获取的示例图像(a)划分为分段平滑区域(b)。 在(c)中显示了每段仿射重构,其中我们可以看到区域之间的人工边界和真实边界被锐化。模糊估计和恢复后,边界变得更加平滑。
3.4 分段平滑图像模型的重要属性
分段平滑图像模型的三个重要属性使我们选择它作为噪声估计和消除模型。 它们是:
1. 分段平滑图像模型与先验稀疏图像一致。
2.由于图像形成的物理定律[25、23、19],每个线段的颜色分布可以通过线段很好地近似。
3. 每个片段的残差标准偏差是该片段中噪声水平的上限。
从等式(3)可以直接得出最后一个属性。 对于前两个属性,我们再次使用图1(a)中的示例图像进行检查。 对于重建图(d),我们计算水平和垂直导数的对数直方图,并将其绘制在图2中。长尾巴清楚地表明,分段平滑重建与自然图像的高峰度统计相匹配[32]。 该图像模型也与枯叶模型[28]有一些相似之处.
对于第二个属性,我们计算每个区域中RGB值{I(v)}的特征值和特征向量。 特征值递减排序并显示在图1(e)中。显然,红色通道占了RGB通道的大部分,这一事实证明了每个段的第一个特征值明显大于第二个特征值。 因此,当我们将像素值投影到第一个特征值而忽略其他两个时,我们在(f)中得到了几乎完美的重构。 原始图像(a)和投影图像(f)之间的均方误差(MSE)为5.31×10-18或PSNR为35.12dB。 这些数字表明,每个段中的RGB值都位于一行中。
在演示了分段平滑图像模型的这些属性之后,我们准备开发用于噪声估计和消除的模型。
4 从单个图像估计噪声
如式(3)所示,尽管图像的每个片段的标准偏差是噪声的上限,但是不能保证片段的均值覆盖图像强度的整个光谱。 此外,标准差的估计本身也是一个具有方差的随机变量。 因此,需要严格的统计框架进行推断。 在本节中,我们介绍了噪声水平函数(NLF)和一种模拟方法来学习先验知识。 提出了一种贝叶斯方法来从单个输入推断噪声水平函数的上限。
4.1了解噪声级的先验
根据定义,可以通过将照相机固定在三脚架上,朝静态场景拍摄多张照片,然后估计与亮度有关的噪声标准偏差,特定品牌照相机的噪声水平函数以及固定参数设置。 对于每个RGB通道的每个像素,计算平均值作为亮度估算值,并计算标准差作为噪声级别。 标准偏差相对于平均值的函数是所需的NLF。 可以通过这种方法获得NLF的地面真相,我们将其用作测试算法的参考方法,但是它既昂贵又费时。
作为替代方案,我们提出了一种基于仿真的方法来获取NLF。 我们为CCD相机的噪声级功能建立模型。 我们介绍了相机噪声模型的术语,显示了噪声水平函数对相机响应函数(也称为CRF,图像亮度与场景照度的函数)的依赖性。 给定相机响应功能,我们可以合成逼真的相机噪点。 因此,从一组参数化的CRF中,我们得出了可能的噪声水平函数集。 NLF的这种受限类别使我们能够从单个图像准确估计NLF。
4.1.1 CCD相机的噪声模型
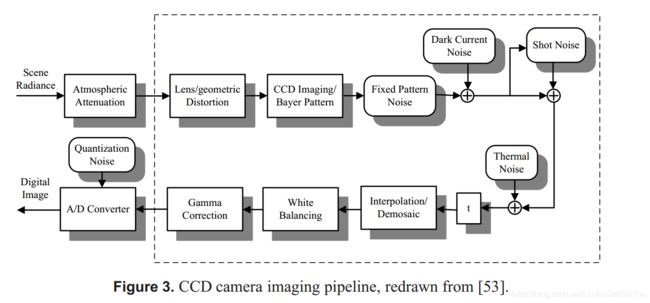
CCD数码相机将辐照度,进入成像传感器的光子转换为电子,最后转换为位。 CCD摄像机的成像管线见图3。 如[24]所述,主要有五个噪声源,即固定模式噪声,暗电流噪声,散粒噪声,放大器噪声和量化噪声。 这些噪声项在[53]中得到了简化。 根据[53]中的成像方程,我们提出以下CCD相机的噪声模型 (4)其中,I是观察到的图像亮度,f(·)是相机响应在函数(CRF)中,ns表示所有依赖于辐照度L的噪声分量,nc表示伽玛校正之前的独立噪声,nq是附加的量化和放大噪声。 由于n q是摄像机附带的最小噪声,并且大多数摄像机可以实现非常低的噪声,因此在我们的模型中将忽略n q。 我们假设噪声统计量
(4)其中,I是观察到的图像亮度,f(·)是相机响应在函数(CRF)中,ns表示所有依赖于辐照度L的噪声分量,nc表示伽玛校正之前的独立噪声,nq是附加的量化和放大噪声。 由于n q是摄像机附带的最小噪声,并且大多数摄像机可以实现非常低的噪声,因此在我们的模型中将忽略n q。 我们假设噪声统计量 ,
, 。 注意ns的方差对辐照度L的线性依赖性[53]。
。 注意ns的方差对辐照度L的线性依赖性[53]。
4.1.2相机响应函数(CRF)
相机响应功能可对CCD相机中的非线性过程进行建模,该过程执行灰度(gamma)和白平衡校正[41]。 给定一组在不同曝光下拍摄的图像,有许多方法可以估算相机的响应函数。 为了探究许多不同CRF的共同特性,我们从http://www.cs.columbia.edu/CAVE [201]下载了201个实际响应函数。请注意,由于不饱和曲线大部分是合成的,因此我们仅选择了190个饱和CRF。 每个CRF是一个1024维向量,代表离散化的[0,1]→[0,1]函数,其中辐照度L和亮度I均被归一化为[0,1]。 我们使用符号crf(i)表示数据库中的第i个函数。
4.1.3合成CCD噪声
原则上,我们可以设置光学实验以针对每台摄像机精确测量噪声水平如何随图像亮度变化。 但是,这将很耗时,并且可能仍无法充分采样相机响应功能的空间。 相反,我们使用数值模拟来估计噪声函数。 基本思想是通过逆相机响应函数f -1变换图像I,以获得辐照平面L。然后,我们将L穿过图3中的处理块,以获得有噪图像IN。
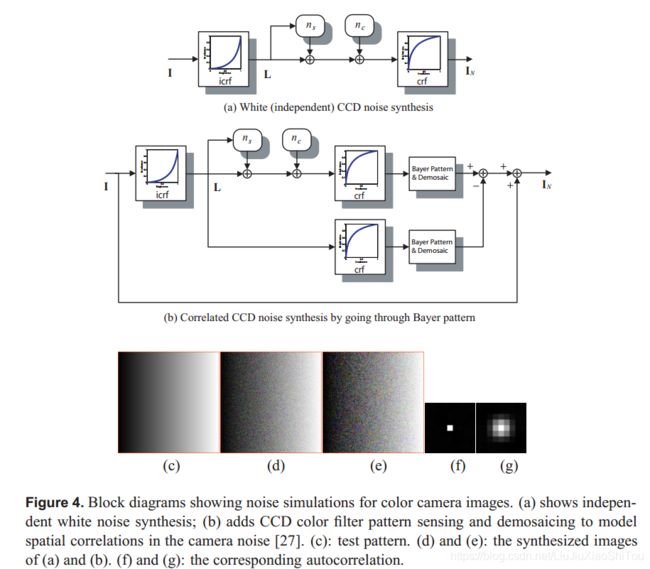
从Eqn直接获取。 (4)是将I反向转换为辐照度L,将噪声独立地添加到每个像素,然后转换为亮度以获得IN。 此过程如图4(a)所示。测试图(c)的合成噪声图像如图(d)所示。
但是,实际的CCD噪声不是白色的。 通过“去马赛克” [38]引入了空间相关性,即从在CCD的滤色器阵列下测量的单色样本在每个像素处重建三种颜色。 我们针对常见的彩色滤光片图案(Bayer)和去马赛克算法(基于梯度的插值[27])模拟了这种效果; 我们期望其他滤波器模式和去马赛克算法将提供可比的噪声空间相关性。 我们根据4(b)合成了CCD相机噪声,并取下了有和无噪声去马赛克图像之间的差异,并将其添加到原始图像中以合成CCD噪声。 合成噪声如图4(e)所示。 噪声图像(d)和(e)的自相关函数分别显示在(f)和(g)中,这表明模拟的CCD噪声在考虑去马赛克效果后显示出空间相关性。
4.1.4噪声级函数的空间
我们将噪声水平函数(NLF)定义为噪声标准偏差相对于图像强度的变化。 该函数可以计算为
其中IN是观测值,而I = E(IN)。 本质上,这是标准偏差相对于平均值如何变化的函数。
基于CCD相机的噪声模型Eqn。 (4)和噪声合成过程中,IN是一个随机变量,取决于相机响应函数f和噪声参数σs和σc。 因为![]() ,所以噪声电平函数也可以写成 其中IN(·)是噪声合成过程
,所以噪声电平函数也可以写成 其中IN(·)是噪声合成过程
![]()
对于红色,绿色和蓝色通道,我们使用数值模拟来估计给定f,σs和σc的噪声函数。 此过程如图5所示。图4(c)中平滑变化的模式用于估计Eqn。 (6)。 为了减少统计波动,我们使用尺寸为1024×1024的图像,并对每个估计取20个样本的平均值。
为了表示噪声级函数的整个空间,我们从f,σs和σc的空间中绘制τ(·; f,σs,σc)的样本。 下载的190个CRF用于表示f的空间。 我们发现σs= 0.16和σc= 0.06会导致很高的噪声,因此将这两个值设置为两个参数的最大值。 我们以0.02步长从0.00到0.16采样σs,以0.01步长从0.01到0.06采样σc。 我们得到了稠密的NLF样本集{τi} K i = 1,其中K = 190×9×6 = 10,260。使用主成分分析(PCA),我们得到了平均噪声水平函数τ,特征向量{wi} mi = 1,相应的特征值{υi} mi = 1。
因此,噪声函数可以表示为
其中系数βi是高斯分布βi〜N(0,υi),且该函数在任何地方都必须为正,即
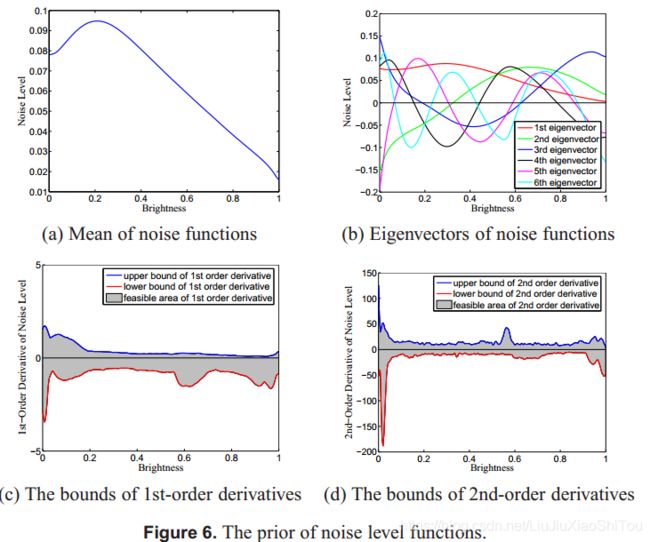
其中![]() 。这种不等式约束意味着噪声函数位于β空间中的圆锥体内。 平均噪声函数和特征向量分别显示在图6(a)和(b)中
。这种不等式约束意味着噪声函数位于β空间中的圆锥体内。 平均噪声函数和特征向量分别显示在图6(a)和(b)中
特征向量用作对函数施加平滑度的基础函数。 我们还对一阶和二阶导数施加14的上限和下限,以进一步约束噪声函数。
设![]() 为一阶和二阶导数的矩阵[46]。 约束可以表示为
为一阶和二阶导数的矩阵[46]。 约束可以表示为
4.2 似然估计
由于每个段的估计标准偏差是对噪声水平的高估,因此我们通过将下包络拟合到标准偏差相对于每个RGB通道平均值的样本中来获得噪声水平函数的上限估计。 这些采样点的示例如图8所示。我们可以简单地将噪声函数拟合到学习空间中,使其位于所有采样点的下方,但仍靠近它们。 但是,由于每个段中的方差估算值都很嘈杂,因此,由于异常值太高,很难对这些估算值进行抽取会导致偏差。 取而代之的是,我们遵循概率推断框架,以使每个数据点都有助于估计。
假设来自k个像素的估计噪声标准偏差为σˆ,其中σ为真实标准偏差。 当k大时,卡方分布的平方根约为![]() [12]。 此外,我们假设大k值是非信息先验,并在给定σˆ的情况下获得真实标准差σ的后验:
[12]。 此外,我们假设大k值是非信息先验,并在给定σˆ的情况下获得真实标准差σ的后验:
令标准正态分布的累积分布函数为Φ(z)。 然后,给定估计值(I,σˆ),基础标准偏差σ大于u的概率为
为了使噪声水平函数适合样本的下包络,我们将亮度[0,1]的范围离散为均匀的间隔![]() 。 我们表示集合
。 我们表示集合![]()
![]() ,并找到方差最小的对
,并找到方差最小的对![]() 。 较低的包络线意味着拟合函数应尽可能低于所有估计值,同时尽可能接近样本。 在数学上,似然函数是在给定特定噪声水平函数的情况下看到观察到的图像强度和噪声方差测量值的概率。 公式为
。 较低的包络线意味着拟合函数应尽可能低于所有估计值,同时尽可能接近样本。 在数学上,似然函数是在给定特定噪声水平函数的情况下看到观察到的图像强度和噪声方差测量值的概率。 公式为
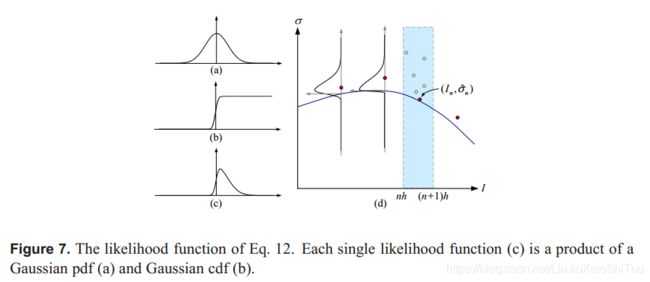
其中s是控制函数应接近样本的程度的参数。 该似然函数如图7所示,其中每个项(c)是方差为s2(a)的高斯pdf与方差为σn2(b)的高斯cdf的乘积。 红点是每个间隔中最小值的样本。 给定函数(蓝色曲线),每个红点都可能超出(c)中带有pdf的曲线,但接近该曲线。
4.3贝叶斯MAP推断
我们要推论的参数实际上是RGB通道噪声水平函数的特征向量![]()
![]() 的系数。 我们表示样本集适合
的系数。 我们表示样本集适合![]() 。 贝叶斯推论证明是一个优化问题
。 贝叶斯推论证明是一个优化问题
在上式中,矩阵![]() 包含主成分,en是E的第n行,并且
包含主成分,en是E的第n行,并且![]() 是对角特征值 矩阵。 目标函数中的最后一项解释了RGB通道的NLF的相似性。 它们的相似性定义为一阶和二阶导数上的距离。 由于优化的维数很低,因此我们使用MATLAB标准的非线性约束优化函数fmincon进行优化。 该功能能够为我们测试的所有示例找到最佳解决方案。
是对角特征值 矩阵。 目标函数中的最后一项解释了RGB通道的NLF的相似性。 它们的相似性定义为一阶和二阶导数上的距离。 由于优化的维数很低,因此我们使用MATLAB标准的非线性约束优化函数fmincon进行优化。 该功能能够为我们测试的所有示例找到最佳解决方案。
4.4 噪声估计的实验结果
我们已经对合成噪声图像和真实噪声图像进行了实验,以测试所提出的噪声估计算法。 首先,我们将3.3节中的CCD噪声合成算法应用于从伯克利图像分割数据库[31]中随机选择的17张图片中,以生成合成测试图像。 为了产生合成CCD噪声,我们指定一个CRF以及两个参数σs和σc。 根据这些信息,我们还将使用第4.1.4节中的训练数据库来生成地面真实噪声水平函数。 在本实验中,我们选择crf(60),σs= 0.10,σc= 0.04。 然后,我们应用我们的方法从合成的噪声图像中估计NLF。 L2和L∞范数都用于测量估计的NLF和地面真实情况之间的距离。 表1列出了这两个规范下的误差统计,其中地面实况的平均值和最大值分别为0.0645和0.0932。
图8中显示了一些估计的NLF。在(a)中,我们观察到许多纹理区域,尤其是在高强度值时,这意味着高信号方差。 尽管高强度样品的估计曲线(红色,绿色和蓝色)与真实噪声函数(灰色)略有不同,但它们并没有紧紧跟随样品的下包络线。 在(b)中,样本没有覆盖整个强度范围,因此我们的估计仅在样本出现的地方可靠。 这显示了现有模型的局限性:假设样本分布良好。 如果颜色分布跨越整个光谱范围并且存在无纹理区域,则估计是可靠的,如(c)所示
我们进行了进一步的实验,以进行完整性检查。 我们使用CanonTMEOS 10D(ISO 1600,曝光时间1/30 s和光圈f / 19)拍摄了29张静态场景的图像,并计算出平均图像。 图9(a)中显示了一个示例。 样品(a)和均值图像的特写视图分别显示在(b)和(c)中。 显然,平均图像中的噪声明显降低了。 使用29张图像的方差作为平均强度的函数,我们计算了“地面真实” NLF,并将其与我们的方法从仅一张图像估计的NLF进行了比较。 每个色带中的NLF之间的一致性非常好,请参见图9(d)。
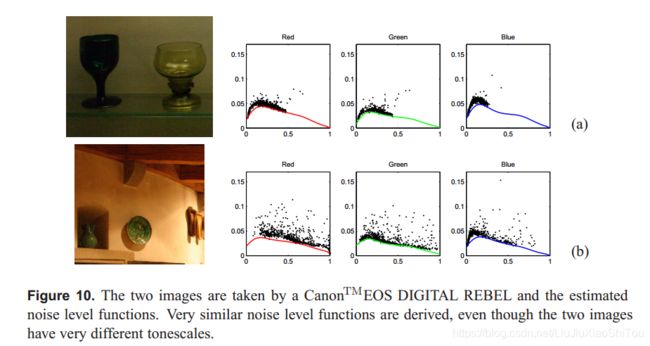
我们还将该算法应用于从CCD摄像机拍摄的其他图像中估计噪声水平的函数。 我们基于可重复性评估了我们的结果:同一相机在同一日期使用相同设置拍摄的照片应具有相同的噪点级别功能,而与图像内容无关。 我们收集了两张佳能TM EOS DIGITAL REBEL拍摄的照片,并估算了相应的噪声级功能,如图10(a)和(b)所示。 即使图像(a)缺少高强度值,估计的NLF也是相似的。
5 基于分割的降噪
从3.2节回想起,观测值I(v)分解为信号s(v)和噪声n(v)。 给定上一节中估计的噪声特征,我们现在准备将信号和噪声与观测值分开。
5.1 0阶模型
令![]() 为分段Ω图像对输入图像I的分段平滑图像重构后的平均颜色。假设噪声与RGB通道无关,我们获得该段中噪声的协方差矩阵
为分段Ω图像对输入图像I的分段平滑图像重构后的平均颜色。假设噪声与RGB通道无关,我们获得该段中噪声的协方差矩阵
从噪声和信号的独立性假设,我们获得(从等式(2))
估计的Σˆs可能不是正定的。 对于这种情况,我们只需将∑ˆs的最小特征值强制为一个小值(0.0001)。
我们仅对每个像素运行贝叶斯MAP估计,即可根据获得的二阶统计量来估计噪声。
其中f(v)是分段平滑重构,最优估计具有简单的封闭形式解
它仅使用协方差矩阵作为权重将像素值从I(v)缩小到f(v)。 对于缩放的身份∑ˆ n,很容易表明,沿颜色协方差矩阵中每个主方向的衰减为![]() ,其中λi是第i个方向的方差。 定性地,当此方差趋于零时(由于非主导方向的方差低,或者该区域没有纹理),清理后的残差逐渐减弱。
,其中λi是第i个方向的方差。 定性地,当此方差趋于零时(由于非主导方向的方差低,或者该区域没有纹理),清理后的残差逐渐减弱。
等式(20)适用于每个像素,其中∑ˆ n和∑ˆ s因段而异。由于在该模型中没有像素的空间关系,因此我们将其称为0阶模型。 使用0阶模型进行去噪的示例如图11所示,其中该算法通过合成AWGN(噪声水平为5%和10%)进行了测试。 显然,0阶模型可以显着消除色噪的色度分量。 对于5%的噪声水平,该结果是可以接受的,并且由于存在空间相关性,我们可以看到相邻段之间的噪声为10%的不连续性。
5.2一阶高斯条件随机场
相邻像素的值在自然图像中相关。 我们选择在Markov随机场(MRF)[18]上使用条件随机场(CRF)[26,47]进行正则化,其中空间相关性是输入图像局部斑块的函数。 在[40]中对图像进行建模,而且,由于所有能量函数都是二次函数,因此我们将其建模为高斯CRF。 我们称其为一阶模型,因为空间相关性是由一阶导数滤波器捕获的。 同样,我们可以具有二阶模型甚至更高阶的模型。 但是我们发现一阶模型足以完成去噪任务。
在上式中,![]() 是s与滤波器φj卷积的滤波器响应。对于此一阶GCRF,我们选择水平和垂直滤波器(即m = 2)。 w(v)和ξi都是权重,以平衡空间相关性的重要性。 ξi是每个线段的权重。我们发现ξi可以是段Ωi中平均噪声水平的线性函数。 w(v)是从原始图像的滤波器响应中得出的。 直观地,当在v处有清晰的边界以弱化空间相关性时,w(v)应该较小;而当没有边界以增强空间相关性时,w(v)应该较大。 边界可以通过Canny边缘检测来检测[6],但是我们发现,当w(v)设置为局部滤波器响应的函数时,该算法更加稳定。 我们使用定向拉长的Gabor正弦和余弦滤波器[17]来捕获底层无噪声图像的边界能量。 边界能是所有取向和sin / cos相的总和。 然后,我们使用非线性函数将能量映射到权重矩阵的局部值,即y =(1- tanh(t1x))t2,其中t1 = 0.6,t2 = 12。 求解方程式(21)等效于求解线性系统,可以通过共轭梯度方法有效地计算出该线性系统,该共轭梯度方法只需要迭代线性滤波即可。
是s与滤波器φj卷积的滤波器响应。对于此一阶GCRF,我们选择水平和垂直滤波器(即m = 2)。 w(v)和ξi都是权重,以平衡空间相关性的重要性。 ξi是每个线段的权重。我们发现ξi可以是段Ωi中平均噪声水平的线性函数。 w(v)是从原始图像的滤波器响应中得出的。 直观地,当在v处有清晰的边界以弱化空间相关性时,w(v)应该较小;而当没有边界以增强空间相关性时,w(v)应该较大。 边界可以通过Canny边缘检测来检测[6],但是我们发现,当w(v)设置为局部滤波器响应的函数时,该算法更加稳定。 我们使用定向拉长的Gabor正弦和余弦滤波器[17]来捕获底层无噪声图像的边界能量。 边界能是所有取向和sin / cos相的总和。 然后,我们使用非线性函数将能量映射到权重矩阵的局部值,即y =(1- tanh(t1x))t2,其中t1 = 0.6,t2 = 12。 求解方程式(21)等效于求解线性系统,可以通过共轭梯度方法有效地计算出该线性系统,该共轭梯度方法只需要迭代线性滤波即可。
6 图像去噪的实验结果
我们的自动图像去噪系统由两部分组成:噪声估计和去噪。 为了与其他降噪算法进行合理比较,我们首先使用具有恒定已知噪声水平(σ)的合成AWGN测试降噪算法。 然后,使用受实际CCD相机噪声污染的图像对整个系统进行测试。
6.1合成AWGN
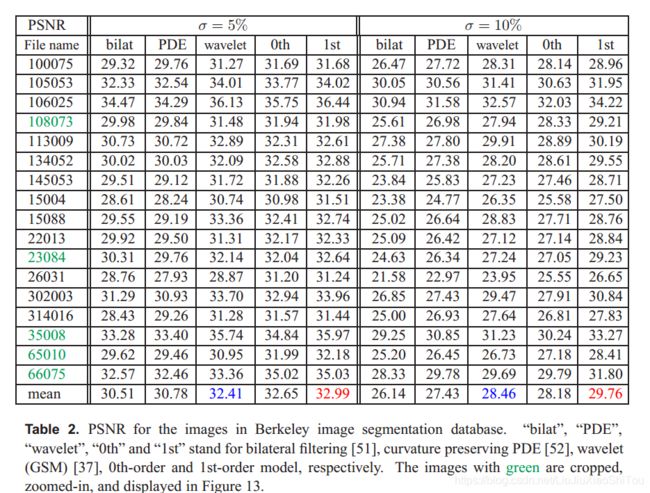
我们从伯克利分割数据集中选择了17张覆盖不同类型的对象和场景的图像[31],并添加了5%和10%噪声水平的AWGN以测试我们的降噪算法。 噪声水平为10%的噪声污染图像如图12所示。我们还运行了标准的双边滤波[51](我们的实现),曲率保留PDE [52](可公开获得的实现2)和小波联合取芯GSM [37]( 公开实施3)。 默认参数设置用于下载的代码。 对于保留曲率的PDE,我们对参数进行了调整,发现通过将alpha = 1,对σ= 10%设置为iter = 4和对σ= 5%进行alpha设置为0.5 iter = 7可以获得最佳结果。 我们使用图13和14的目视检查以及表2的峰值信噪比(PSNR)统计数据将其结果与自己的结果进行比较。
显然,我们的技术始终优于双边滤波,保留曲率的PDE和小波联合取芯。 在PSNR方面,我们的技术明显优于这些算法。 当σ= 0.05时,即噪声水平较低时,即使是0阶模型也要优于最新的小波GSM。 当σ= 0.10时,即噪声水平高时,一阶模型的平均性能比小波GSM高1.3 PSNR。
还在图13中从(a)到(e)视觉检查了结果,分别对应于图12中的图像35008、23084、108073、65010和66075。 去噪结果的一些特写视图如图14所示。保留曲率的PDE方法在强边缘周围生成彩色边缘伪影。 小波取芯倾向于产生颜色和模糊的伪像,尤其是在(a)和(d)中。 但是,我们的算法能够平滑平坦的区域,保留锐利的边缘,并保留细微的纹理细节。 在图13和14(a)中,我们的算法实现了虫子的更清晰边界,并保留了花朵的纹理。
在(b)中,许多具有各种宽度的曲线都得到了很好的重构,而小波取芯在边界周围引入了彩色边缘伪影。 在(c)中,根据我们的算法,老虎的胡须变得更加清晰明了,草的茎和叶也变得更加清晰。 在(d)中,保留了叶子的纹理细节,同时使云团得到了很好的平滑。 (e)中的鸵鸟头是一个失败的例子,其中上颈部分过度光滑,并且为毛茸茸的边缘生成了一些人工边界。 请注意,我们的系统并不总是完全消除纹理区域的噪音,但是由于消除了噪音的色度分量,因此在视觉上看起来令人愉悦。 另外,如(d)中的纹理区域中的残留噪声不明显。
总体而言,在合成噪声情况下,我们的算法优于最新的去噪算法。 我们未优化的MATLABTM实现平均需要不到一分钟的时间来对Berkeley数据库中的一张图片(典型分辨率为481×321)进行降噪。我们的实验是在2.8 GHz奔腾D PC上运行的。
6.2实际CCD噪声
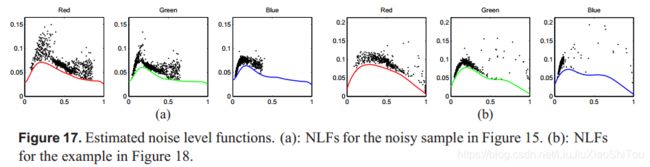
我们使用CCD相机拍摄的图像(噪声明显)进一步测试了自动降噪系统[35]。 图15(a)中的照片是由CanonTMEOS DIGITAL REBEL拍摄的,暗像素的噪声很大,而亮像素的噪声很小。 噪声水平函数被估计并显示在图17中,与观察结果一致。 为了进行比较,我们还运行了小波取心(GSM),σ= 10%,σ= 15%,结果分别如图15(b)和(c)所示。 我们的系统自动生成的降噪结果显示在(d)中。 这些结果的特写检查如图16所示。显然,在恒定噪声水平假设的情况下,小波取芯算法无法平衡高噪声区域和低噪声区域。 当σ= 10%时,对于边缘较锐利的明亮像素,效果更好;当σ= 15%时,对于具有较平滑区域的暗像素,效果更好。 但是总的来说,我们仍然可以看到块状的颜色伪像,过度平滑的边界和纹理细节的丢失。 我们的系统产生的结果成功克服了这些问题。
在图16行(1)中,我们的方法产生几乎平坦的补丁。 在第(2)行中,边界更加清晰,而在第(3)行中,保留了许多细微的纹理细节。 总体而言,我们的算法在视觉上产生了更具吸引力的结果(我们无法计算PSNR,因为没有地面真实的28幅清晰图像)。
我们在图18(a)所示的另一个具有挑战性的示例上测试了我们的算法。 如(b)所示,由于色噪声的空间相关性,小波取芯不能有效地去除色噪声。 即使我们在(c)中的自动降噪系统产生的结果过分锐化了边缘,使其具有卡通风格,但噪点却被完全消除,图像看上去更加悦目。
由于我们的分割算法会为平坦区域生成较大的片段,为纹理区域生成较小的片段,因此,如果分割参数设置在合理范围内,则不会显着影响系统的整体性能。 我们对基准测试使用了相同的参数设置,并且发现如果允许更大的段,则图18中的实际CCD噪声示例在视觉上会获得更令人满意的结果(不幸的是,我们无法测量PSNR)。 当然,更好的分割将进一步改善去噪系统,但是我们目前的分割算法已足够。
7 讨论
在使用合成噪声和真实噪声展示了我们模型的成功之后,我们想对去噪问题和建模提供一些见解。
7.1 彩色噪声
如第3节所示,段中像素的颜色大致沿三维RGB空间的1D子空间分布。 这与以下事实是一致的:强的尖锐边界主要是由材料(或反射率)的变化产生的,而弱的平滑边界主要是由照明的变化产生的[48]。 由于人类视觉系统已经习惯了这些模式,因此打破一维子空间规则的色噪声在我们的眼睛中显得很烦人。 我们基于此一维子空间规则设计了降噪系统,以有效去除色彩噪声的色度分量。 图11中0阶模型的结果表明,去除色度分量后,图像看起来更加令人愉悦。
7.2 条件模型与生成模型
在我们的系统中,我们仅进行一次分割即可获得输入图像的分段平滑模型。 如果我们将区域分区视为生成噪声图像的隐藏变量,则条件模型将变为生成模型29。 生成模型的推论将需要在区域分区上进行整合。 凭直觉,嘈杂的输入图像的分割可能是嘈杂且不可靠的,并可能导致许多可能的分割。
这种完整的贝叶斯方法的一种方法是从输入图像中采样分区,为每个分割获取去噪图像,然后计算平均值作为输出。 这种方法可能会通过除去一些边界伪像来改善结果,但是由于分区的巨大空间,因此在实践中很难解决。 另一种方法是将分区视为丢失的数据,并使用期望最大化(EM)算法在基于去噪图像对图像进行分割(E步)与基于分割对噪声图像进行估计(M步)之间进行迭代 。 由于需要多次迭代,因此该方法在实践中也很棘手。 尽管如此,这些完整的贝叶斯方法可能是未来基于分割的图像处理系统具有更强大计算能力的有希望的方向。
7.3 计算机视觉系统的自动化
计算机视觉系统的性能对外围参数敏感,例如,噪声水平,模糊水平,分辨率/图像质量,照明和视点。 例如,对于图像去噪,噪声水平是系统的重要参数。 错误估计噪声电平可能会产生不良结果。 现有的大多数计算机视觉算法都专注于解决已知外围参数的问题,但是必须对算法进行调整以适合不同的成像条件。 因此,使计算机视觉系统将重要的外围参数完全自动化是一个重要的方向。我们的自动图像降噪系统是使降噪算法对噪声水平具有鲁棒性的首次尝试之一。
8 总结
基于一个简单的分段平滑图像先验,我们提出了一种基于分割的方法来自动估计和消除彩色图像中的噪声。 通过估计每段图像方差的标准偏差的下包络线来获得NLF。 通过将RGB像素值投影到适合每个段的色彩空间中的一条线上,可以显着消除色彩噪声的色度。 通过制定和求解高斯条件随机场来消除噪声。 进行实验以测试噪声估计和去除算法。
我们通过以下三种方法验证了估计的噪声水平是真实噪声水平的严格上限:(1)通过与重复测量同一张图像的实验测量的噪声显示出良好的一致性,(2)通过重复测量相同的NLF 同一台相机处理不同的图像内容,以及(3)通过准确估算已知的合成噪声函数。
我们的噪声估计算法不仅可以应用于降噪算法,而且可以应用于其他计算机视觉应用,以使其与噪声水平无关[29]。通过生成整形器边缘,产生更平滑的平坦区域并保留细微的纹理细节,我们的去噪算法在合成图像和实际受噪声污染的图像上均优于最新的小波去噪算法。 这些功能符合我们为良好的降噪算法提出的原始标准。