快速、归并、计数排序算法（Java）

快速排序算法(Quick Sort)

基本思想

通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

算法步骤

1、设置第一个元素值为基准值key，将数列中比key小的数放到key左边并重新组成一个新数列r_left，比key大的放到其右边重新组成一个数列r_right。

2、重复第一个步骤，递归地对子序列r_left和r_right进行划分，直至所有数列都为空数列，排序结束。

举例说明

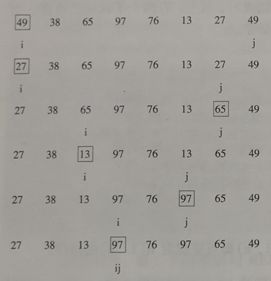
对 r [ ] =｛49，38，65，97，76，13，27，49｝进行从小到大排序。

1、令key = r[0] = 49，并设置左右指针 i 和 j ，分别指向数列的最左端和最右端；

2、指针 j 向左滑动，直至 r[j] < key，则令 r[i] = r[j]，且 i++；

3、指针 i 向右滑动，直至 r[i] > key，则令 r[j] = r[i]，且 j++；

4、重复步骤2、3，直至 i = j，则令 r[i] = key，第一次划分结束；

  第一次划分的结果：[27 38 13] 49 [76 97 65 49]

  子序列 r_left ：27 38 13

  子序列 r_right ：76 97 65 49

5、对子序列重复步骤1~4，继续划分子序列，直到所有子序列为空序列，则排序结束。

  第二次划分的结果：[13] 27 [38] 49 [49 65] 76 [97]

  第三次划分的结果：13 27 38 49 49 [65] 76 97

  第四次划分的结果：13 27 38 49 49 65 76 97  //排序结束

时间与空间复杂度

• 时间复杂度：

  • 最好情况：O(nlogn)
  • 最坏情况：O(n^2)
  • 平均情况：O(nlogn)

• 空间复杂度：O(logn)

快排算法的空间复杂度是固定的，但时间复杂度根据实际情况而变。因此，在实际情况中，我们要先分析要进行排序的数列的特征，再选择合适的排序算法。

最好的情况：每次划分所选择的中间数恰好将当前序列几乎等分，经过 logn 趟划分，便可得到长度为1的子表。

最坏情况：每次所选的中间数是当前序列中的最大或最小元素，这使得每次划分所得的子表中一个为空表，另一子表的长度为原表的长度 -1。

归并排序算法(Merge Sort)

基本思想

将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

算法步骤

1、先将数列一直对半分成多个子数列，直到所有子数列都为有序序列或者子数列只有一个元素；

2、对所有的子序列进行并归。

时间与空间复杂度

• 时间复杂度：O(nlogn)
• 空间复杂度：O(n)

归并排序的时间复杂度，在前面中提到的最坏，最好和平均情况下都是O(nlogn)（与快速排序的最好情况相同），这说明它性能非常好的排序算法。

但是它需要占用 O(n)的内存空间，如果数据量一旦很大，内存可能吃不消。而快速排序算法是就地排序算法，不占用额外的内存空间。针对占用内存问题，目前好像有方法已经可以将归并排序算法改进为就地排序算法，大家可以先自行了解一下。

计数排序算法(Counting Sort)

基本思想

对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定）。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。

算法步骤

1、找出数列中的最小值min与最大值max，确定数值区间 [min,max] 并求出数值组长度 k=max-min+1；

如｛9，4，4，1｝：min=1，max=9，区间 [1,9]，长度 k=9

2、标记各个数值在要排列数列中的出现次数；

[1,9] 每个数值出现的次数 d[ ] =｛1，0，0，2，0，0，0，0，1｝

3、根据每个数值 i 出现的次数d[i]，依次输出d[i]个相应数值，即可得到排序结果。

最后输出排序结果：1 4 4 9

时间与空间复杂度

• 时间复杂度：O(n+k)
• 空间复杂度：O(n+k)

其中 k=max-min+1 为区间长度。

由于计数排序是一种非比较排序算法，它的优势在于在对一定范围内的整数排序时，快于任何比较排序算法（如前面的快速排序与归并排序）。当k不是很大并且序列比较集中时，计数排序是一个很有效的排序算法。

如果 k 很大，则需要申请大量的空间来存储数值区间内每个数值在数列中出现的次数d[ ]。在这种情况下，不适合使用计数排序算法。

java代码

话不多说，直接给出代码。

public class quickSort {
	public static void main(String[] args) {
		long startTime = System.nanoTime();//测时间：currentTimeMillis表示毫秒，nanoTime表示纳秒
		int[] arr= {6, 9, 1, 4, 5, 8, 7, 0, 2, 3, 100};
		int right=arr.length-1;
		quickSort(arr, 0, right);
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i]+" ");
		}
		long endTime = System.nanoTime();//测时间
		System.out.println("\n用时："+(endTime - startTime)+"ns");
	}
	public static void quickSort(int[] arr, int left, int right) {
		if(right==left)
			return;
		int key=arr[left];
		int high=right;
		int low=left;
		while(left<right) {
			while(arr[right]>key&&left<right) {
				right--;
			}
			arr[left]=arr[right];
			left++;
			while(arr[left]<key&&left<right) {
				left++;
			}
			arr[right]=arr[left];
			right--;
		}
		arr[left]=key;
		quickSort(arr, low, left-1);
		quickSort(arr, right+1, high);
	}
}

public class mergeSork {
	public static void main(String[] args) {
		long startTime = System.nanoTime();
		int []arr= {6, 9, 1, 4, 5, 8, 7, 0, 2, 3, 100};
		int right=arr.length-1;
		mergeSork(arr, 0, right);
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i]+" ");
		}
		long endTime = System.nanoTime();
		System.out.println("\n用时："+(endTime - startTime)+"ns");
	}
	
	public static void mergeSork(int []arr, int left, int right){
		if(right==left) {
			return;
		}
		int mid=(left+right)/2;
		mergeSork(arr, left, mid);
		mergeSork(arr, mid+1, right);
			
		int []a=new int[arr.length];
		int k=left;
		int p1=left;
		int p2=mid+1;
		while(p1<=mid&&p2<=right) {
			if(arr[p1]<arr[p2])
				a[k++]=arr[p1++];
			else 
				a[k++]=arr[p2++];
		}
		while(p1<=mid) 
			a[k++]=arr[p1++];
		while(p2<=right) 
			a[k++]=arr[p2++];
		for (int i = left; i <= right; i++) {
			arr[i]=a[i];
		}
	}
}

public class countingSort {
	public static void main(String[] args) {
		long startTime=System.nanoTime();
		int []arr= {6, 9, 1, 4, 5, 8, 7, 0, 2, 3, 100};
		countingSort(arr);
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i]+" ");
		}
		long endTime=System.nanoTime();
		System.out.println("\n用时："+(endTime - startTime)+"ns");
	}
	
	public static void countingSort(int []arr){
		int min=arr[0],max=arr[0];
		for(int i:arr){
			if(i<min)
				min=i;
			if(i>max)
				max=i;
		}
		int a[]=new int[max-min+1];
		int k[]=new int[max-min+1];
		for(int i=0;i<arr.length;i++) {
			a[i]=min+i;
			k[i]=0;
			for(int j=0;j<arr.length;j++) {
				if(arr[j]==a[i])
					k[i]++;
			}
		}
		int K=0;
		for(int i=0;i<arr.length;i++) {
			for(int j=0;j<k[i];j++) {
				arr[K]=a[i];
				K++;
			}
		}
	}
}

复杂度比较

Quick Sort：397600ns
Merge Sort：222500ns
Counting Sort：224000ns

我在代码中测试了运行时间，本来想对比一下三种算法的时间复杂度，但是由于数列太小，无法作出明显的对比结果。日后有需要的话，我会对它们的时间与空间复杂度作进一步的研究。

如果文中有写得不好或者错误的地方，请大家评判指正，谢谢！