数据结构 - 二叉树、红黑树

目录

一：二叉树

二：满二叉树

三：完全二叉树

四：堆

五：二叉查找树（BST）

六：平衡二叉树

七：红黑树

---

一：二叉树

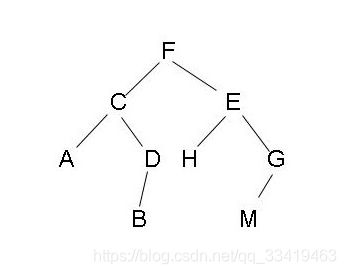
   二叉树是一种数据结构，其每个结点最多有两个子树的树结构。也就是每个节点下面有两个分叉，通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

  最上面的节点称为根节点，相对最下面的节点称之为叶节点。

    一棵深度为k，且有2^k-1个节点的二叉树，称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树。具有n个节点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树，至少有2k-1个叶子节点，至多有2k-1个节点。

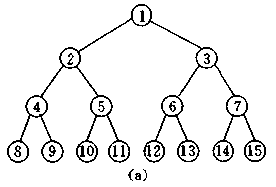
二：满二叉树

  除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树

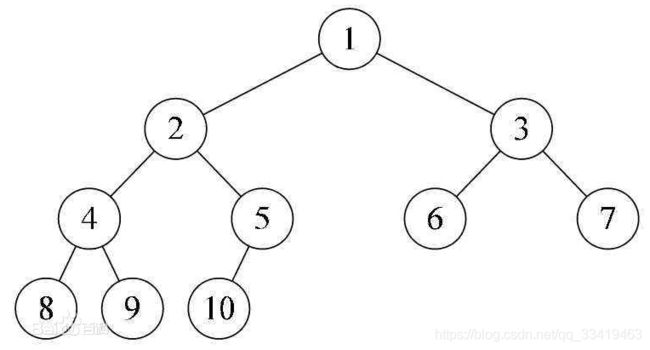
三：完全二叉树

  完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。

  若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树

四：堆

     当一颗二叉树的每个结点都大于等于它的两个子节点时，它被称为堆有序。相应地，在堆有序的二叉树中，每个结点都小于等于它的父节点，从任意结点往上，我们都能得到一列非递减的元素；从任意结点往下，我们都能得到一列非递增的元素。根节点就是堆有序的二叉树中的最大节点。所以说在一个堆有序的二叉树中，父节点的位置是K/2,它的两个子节点的位置是2k,2k+1。这样通过索引的变化，我们就可以在数组中得到不同的元素了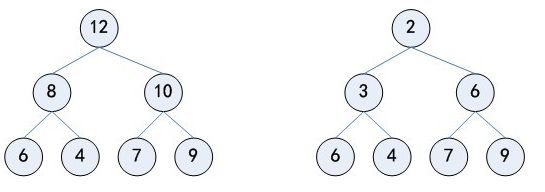

五：二叉查找树（BST）

    二叉查找树（Binary Search Tree），也称有序二叉树（ordered binary tree）,排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树:

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值
3. 任意节点的左、右子树也分别为二叉查找树
4. 没有键值相等的节点（no duplicate nodes）

代码实现如下：

public class BinarySearchTreeSymbolTable : SymbolTables where TKey : IComparable, IEquatable
{
    private Node root;
    private class Node
    {
        public Node Left { get; set; }
        public Node Right { get; set; }
        public int Number { get; set; }
        public TKey Key { get; set; }
        public TValue Value { get; set; }

        public Node(TKey key, TValue value, int number)
        {
            this.Key = key;
            this.Value = value;
            this.Number = number;
        }
    }
...
}

查找操作和二分查找类似，将key和节点的key比较，如果小于，那么就在Left Node节点查找,如果大于，则在Right Node节点查找，如果相等，直接返回Value。主要方法有递归和迭代两种：

递归：

public override TValue Get(TKey key)
{
    TValue result = default(TValue);
    Node node = root;
    while (node != null)
    {

        if (key.CompareTo(node.Key) > 0)
        {
            node = node.Right;
        }
        else if (key.CompareTo(node.Key) < 0)
        {
            node = node.Left;
        }
        else
        {
            result = node.Value;
            break;
        }
    }
    return result;
}

迭代：

public TValue Get(TKey key)
{
    return GetValue(root, key);
}

private TValue GetValue(Node root, TKey key)
{
    if (root == null) return default(TValue);
    int cmp = key.CompareTo(root.Key);
    if (cmp > 0) return GetValue(root.Right, key);
    else if (cmp < 0) return GetValue(root.Left, key);
    else return root.Value;
}

插入和查找类似，首先查找有没有和key相同的，如果有，更新；如果没有找到，那么创建新的节点。并更新每个节点的Number值，代码实现如下：

public override void Put(TKey key, TValue value)
{
    root = Put(root, key, value);
}

private Node Put(Node x, TKey key, TValue value)
{
    //如果节点为空，则创建新的节点，并返回
    //否则比较根据大小判断是左节点还是右节点，然后继续查找左子树还是右子树
    //同时更新节点的Number的值
    if (x == null) return new Node(key, value, 1);
    int cmp = key.CompareTo(x.Key);
    if (cmp < 0) x.Left = Put(x.Left, key, value);
    else if (cmp > 0) x.Right = Put(x.Right, key, value);
    else x.Value = value;
    x.Number = Size(x.Left) + Size(x.Right) + 1;
    return x;
}

private int Size(Node node)
{
    if (node == null) return 0;
    else return node.Number;
}

随机插入形成树的动画如下，可以看到，插入的时候树还是能够保持近似平衡状态：

求最大最小值：

    二叉查找树中，最左和最右节点即为最小值和最大值，所以我们只需迭代调用即可

六：平衡二叉树

平衡二叉搜索树（Self-balancing binary search tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点总数的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列，可以参考Fibonacci(斐波那契)数列，1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。

七：红黑树

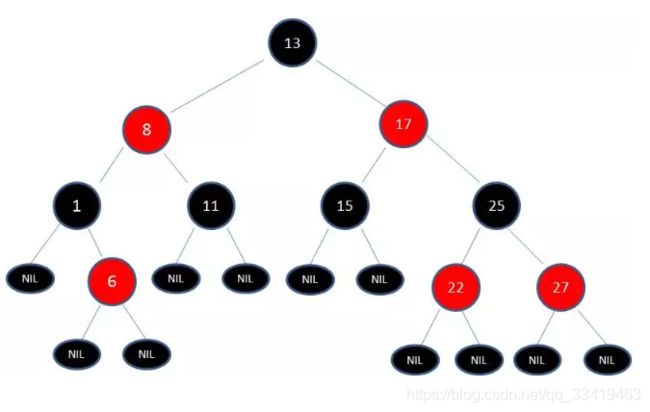
    红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

1. 节点是红色或黑色。
2. 根节点是黑色。
3. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
4. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
5. 从根节点到叶节点，最长的路径不会超过最短路径的2倍

在插入或者删除节点的时候我们需要作出一些调整来确保红黑树的结构，主要的调整方法有三种：

1.变色：

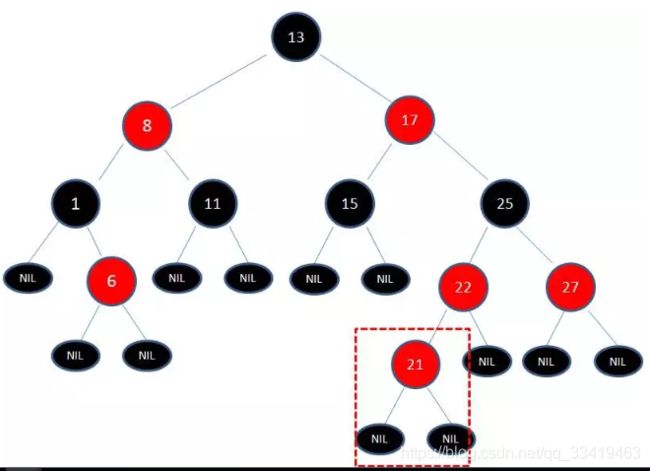
     向原红黑树插入值为21的新节点

发现有两个连续的红色节点，这样就破坏了红黑树的结构，所以我们需要作出一些调整：

接上面的操作，我们变色完了后发现，多了个黑色的节点出来，每条路径的黑色节点数量不能保持一致，因此我们还需要一个调整：

2.左旋转和右旋转

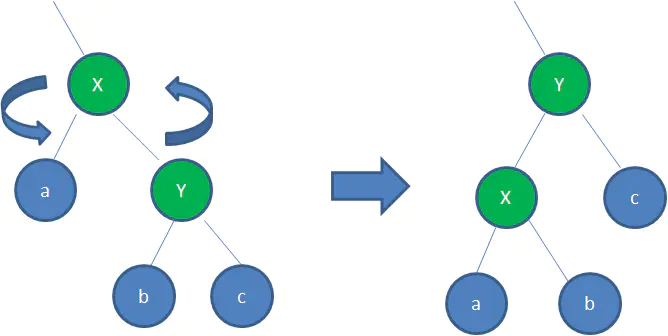
左旋转：逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为自己的左孩子。说起来很怪异，大家看下图：

右旋转：顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子。大家看下图：

以刚才的案例为例：

首先变色：

此时节点17和节点25是连续的两个红色节点，那么把节点17变成黑色节点？恐怕不合适。这样一来不但打破了规则4，而且根据规则2（根节点是黑色），也不可能把节点13变成红色节点。

变色已无法解决问题，我们就要进行旋转 -》 左旋转

由于根节点必须是黑色节点，所以需要变色，变色结果如下：

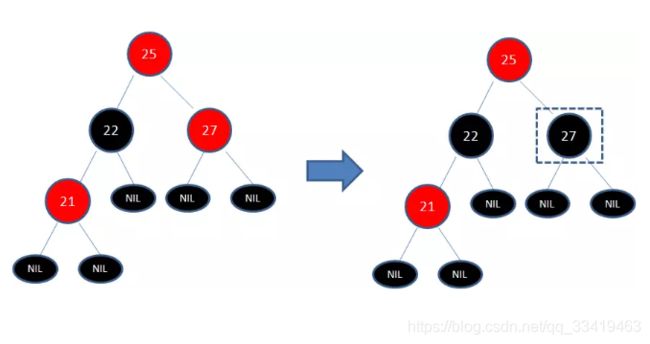
其中两条路径(17 -> 8 -> 6 -> NIL)的黑色节点个数是4，其他路径的黑色节点个数是3，所以我们再进行一次右旋转：

最后变色：

如此一来，我们的红黑树变得重新符合规则。这一个例子的调整过程比较复杂，经历了如下步骤：

变色 -> 左旋转 -> 变色 -> 右旋转 -> 变色

---

JAVA中的TreeMap,TreeSet底层就是红黑树实现的，Java8中HashMap也用到了红黑树。