动态规划法求解背包问题
目录
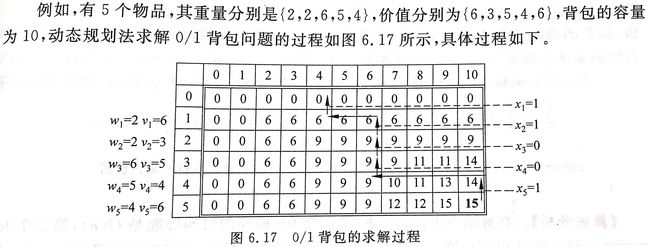
0/1背包问题
完全背包
多重背包
0/1背包问题
#include
#include
#include
#define N 100
#define M 100
#define MAX(a,b) a < b ? b : a
using namespace std;
struct Goods
{
//int id;//物品序号
int weight;//物品重量
int value;//物品价值
};
//N,M随题意变动
Goods goods[N];//物品信息
int dp[N][M];
int X[N];//物品装入情况
int KnapSack(int n, Goods goods[],int C,int X[])//物品种类,物品详情,容量,物品装入情况
{
memset(dp,0,sizeof(dp));
memset(X,0,sizeof(X));
for(int i = 0; i <= n; i++)//初始化第0列
dp[i][0] = 0;
for(int j = 0; j <= C; j++)//初始化第0行
dp[0][j] = 0;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= C; j++)
{
if(j < goods[i-1].weight)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = MAX(dp[i-1][j],dp[i-1][j-goods[i-1].weight] + goods[i-1].value);
}
}
for(int i = n,j = C; i > 0; i--)
{
if(dp[i][j] > dp[i-1][j])
{
X[i-1] = 1;
j = j - goods[i-1].weight;
}
else
X[i-1] = 0;
}
return dp[n][C];
}
int main()
{
int n,C;//物品数量,背包容量
printf("物品种类n:");
scanf("%d",&n);
printf("背包容量C:");
scanf("%d",&C);
for(int i = 0; i < n; i++)
{
printf("物品%d的重量w[%d]及其价值v[%d]:",i+1,i+1,i+1);
scanf("%d%d",&goods[i].weight,&goods[i].value);
}
int value = KnapSack(n,goods,C,X);
printf("动态规划法求解0/1背包问题:\nX=[");
for(int i = 0; i < n; i++)
cout< 完全背包
完全背包和0/1价值背包问题的区别在于每一件物品的数量都有无限个,而0/1背包每件物品数量只有一个。
在递推公式时,注意这里需要考虑放入一个物品i时还可能继续放入i,
所以不能是:dp[i][j] = max(dp[i - 1][j], dp[i-1][j - weight[i]] + value[i]);
需要加以改变:dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
dp[i][j]理解为容量为j的背包,对于前i种物品来讲的最大价值。
#include
#include
#include
#define N 100
#define M 100
#define MAX(a,b) a < b ? b : a
using namespace std;
struct Goods
{
//int id;//物品序号
int weight;//物品重量
int value;//物品价值
};
//N,M随题意变动
Goods goods[N];//物品信息
int dp[N][M];
int X[N];//物品装入情况
int KnapSack(int n, Goods goods[],int C,int X[])//物品种类,物品详情,容量,物品装入情况
{
memset(dp,0,sizeof(dp));
memset(X,0,sizeof(X));
for(int i = 0; i <= n; i++)//初始化第0列
dp[i][0] = 0;
for(int j = 0; j <= C; j++)//初始化第0行
dp[0][j] = 0;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= C; j++)
{
if(j < goods[i-1].weight)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = MAX(dp[i-1][j],dp[i][j-goods[i-1].weight] + goods[i-1].value);
}
}
//计算每个物品放入的个数
for(int i = n,j = C; i > 0; i--)
{
while (dp[i][j] == dp[i][j - goods[i-1].weight] + goods[i-1].value)
{
X[i-1]++;
j = j - goods[i-1].weight;
}
}
return dp[n][C];
}
int main()
{
int n,C;//物品种类,背包容量
printf("物品种类n:");
scanf("%d",&n);
printf("背包容量C:");
scanf("%d",&C);
for(int i = 0; i < n; i++)
{
printf("物品%d的重量w[%d]及其价值v[%d]:",i+1,i+1,i+1);
scanf("%d%d",&goods[i].weight,&goods[i].value);
}
int maxvalue = KnapSack(n,goods,C,X);
printf("动态规划法求解完全背包问题:\nX=[");
for(int i = 0; i < n; i++)
cout< 多重背包
多重背包和01背包、完全背包的区别:多重背包中每种物品的数量是给定的,可能不是一个,绝对不是无限个。
方法:转化为01背包。若有kind中物品,每种物品num个,将这些物品用01背包问题解决。