张量网络算法基础（一、张量和线性代数基础）

这是本人在暑期学习中对有关张量网络算法知识的一些梳理，有什么错误请大家批评指正，喜欢的给点个赞。

一、张量基础

1. 张量的定义

0阶张量（点）----标量(scalar)：0
1阶张量（线）----向量(vector)：[1,2,3,4,5]
2阶张量（面）----矩阵(matrix)：$\left[\begin{array}{ll}1& 0\\ 2& 1\end{array}\right]$
3阶张量（体）----张量(tensor):[[[1,2,3],[4,5,6],[7,8,9]],[[1,2,3],[4,5,6],[7,8,9]],[[1,2,3],[4,5,6],[7,8,9]]]

这样子看起来不是很直观，张量的图形表示更加直观，如下图。从图中我们可以看出，0阶张量就是一个点，就像一个天安门站岗的士兵；1阶张量就是N多个0阶张量排成一行，就像天安门的升国旗对的士兵们排成的一列队伍；2阶张量就像阅兵时那些军人们排出的一个阵列；3阶张量就像每个军区的不同兵种排成的一个大阵列以此类推，N阶张量就是按照如上规律继续进行排列。

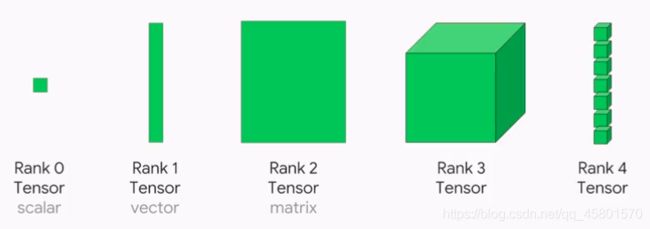
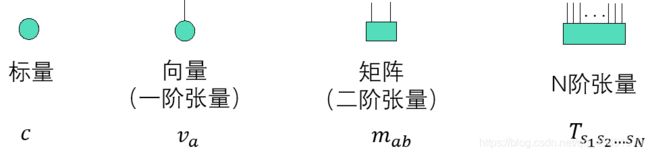
按照上面张量的表示方法，当张量的阶数越高，表示也会越麻烦，于是另外一种用bond来表示阶数的图形表示则会更加简洁，如下图。张量用连着N个腿（bond）的圆圈、方块或者其它图形来表示，每一条腿代表张量的一个阶，N条腿就代表张量有N阶。注意：腿的形状不影响张量的阶数

2. 张量的基本操作和运算

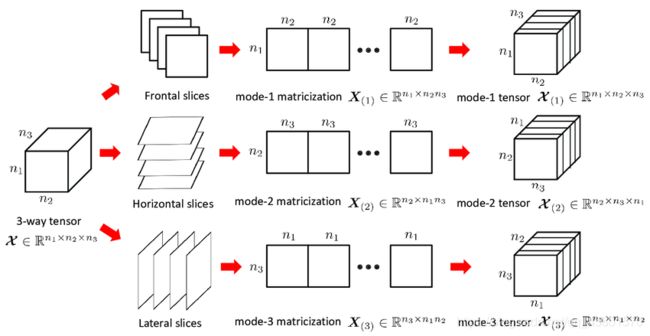
张量可进行切片操作提取相关的元素，以三阶张量为例，如图。切片操作就是在张量中抽取矩阵的操作，保留两个维度的变化。这个方式可能不太好理解，也或多或少有点绕（要是你不觉得绕，当我没说）。

换一种理解方式，我们可以理解为对一个维度进行切割，就像Frontal slices是对$n_3$这个维度进行切割，Horizontal slices是对$n_1$这个维度进行切割，Lateral slices是对$n_2$这个维度进行切割，就像我们平时切豆腐，可以对三个不同的维度进行切割，这一块主要是理解记忆。

切片之后张量的展开自然是不能少的，张量展开通俗点来讲就是把切片之后的张量一片一片拼凑起来，拼凑方式有下图三种，可以$n_1$维度进行拼接，可以$n_2$维度进行拼接，也可以$n_3$维度进行拼接。

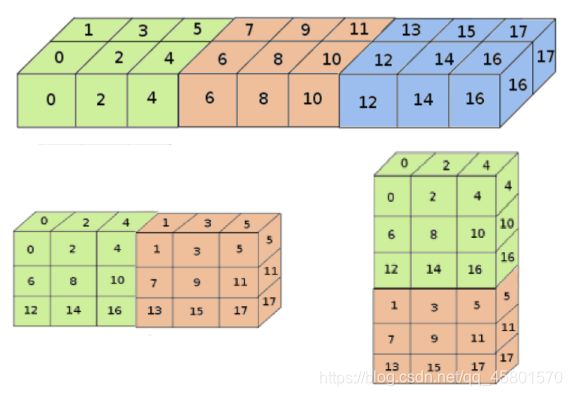
有没有点点的混乱，下面上我们带有数字和颜色的图，配上下图是不是感觉好多了。

张量的基本运算主要有以下几个：
向量的内积：
$$C=\sum _a{x}_a{y}_a$$

向量乘矩阵：
$$v_b=\sum _a{x}_a{M}_{ab}=xM$$

矩阵乘矩阵：
$$M_{ac}=\sum _b{A}_{ab}{B}_{bc}=AB$$

张量的缩并：
$$T_{acde}=\sum _b{A}_{abc}{B}_{bde}$$

由下面的图我们很容易可以看出，只要下标相同，我们就可以把它们缩并，这也是张量运算的核心所在，后面还会遇到很多类似的情况。

二、线性代数基础

1. 本征值分解与最大本征值问题

本征值分解

本征向量与本征值又称特征向量与特征值，相信学过线性代数的小伙伴是不会陌生的。对于给定D × D的方阵M， 设D维归一化向量$v$与标量 $\lambda$ ，当其满足 $\mathbf{M}\mathbf{v}=\mathbf{\lambda }\mathbf{v}$ 时，称$v$与$\lambda$分别为M的本征向量与本征值。本征值分解，又称特征分解（eigenvalue decomposition ) ，满足:
$$M=U\Gamma U^{+}$$

其中 U被称为变换矩阵，其每一列为M的本征向量，且满足正交归一性 $U{U}^{†}=I;\Gamma$ 为对角矩阵，称为本征谱。

最大本征值问题

假设矩阵本征值为实数，求解给定矩阵的最大本征值及其本征态。最大本征值问题对应的优化问题就是对于给定的矩阵$M$，求解归一化向量$v$，使得函数 $\mathrm{f}=\left|{\mathrm{v}}^{\mathrm{T}}\mathrm{M}\mathrm{v}\right|$ 的值极大化,f 对应最大的本征值的绝对值。此证明采用数值证明法，要是小伙伴有其它的好方法评论区留言哦！
数值证明的代码实现：

import numpy as np
import copy
import matplotlib.pyplot as plt#画图

dim=4
M=np.random.randn(dim,dim)
M=M+M.T     #对称化保证本征分解存在   
print(M)

#求本征值和本征向量
lm,u=np.linalg.eig(M)
print("Eigenvalues:\n",lm)
print("Eigenvectors:\n",u)

#求绝对值最大的本征值及其对应的本征向量
n_max=np.argmax(abs(lm))
lm_max=lm[n_max]
v_max=u[:,n_max]
print(v_max)

#f=vMv'
f_max=abs(v_max.dot(M).dot(v_max))
print(f_max)

#随机建立多个归一化向量
num_v=200
vecs=np.random.randn(num_v,dim)
vecs=np.einsum('na,n->na',vecs,1/np.linalg.norm(vecs,axis=1))
#计算每个向量的f
f=abs(np.einsum('na,ab,nb->n',vecs,M,vecs.conj()))
#print(np.ones(num_v,))
#画图展示最大本征值
x=np.arange(num_v)
y=np.ones(num_v,)*f_max
plt.plot(x,y,'-')
plt.plot(x,f,'r')
plt.show()

随机建立200个归一化向量所得到的结果，由图可以看出，当随机生成的归一化向量越多，向量的本征值会越来越靠近最大本征值的绝对值，但永远不会大于最大本征值的绝对值。

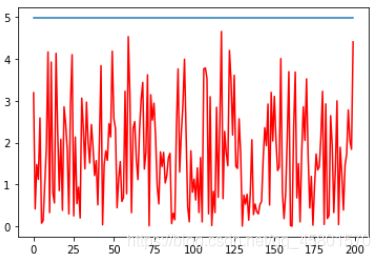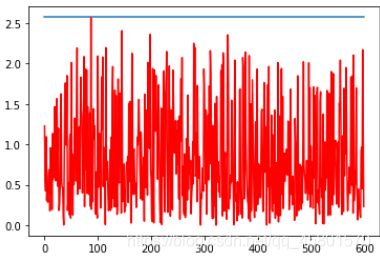num_v=200	num_v=600

最大本征值问题的幂级数求解法

考虑实对称矩阵$M$，设$\Gamma$和u ${}^{(0)}$ 为其绝对值最大的唯一本征值及本征向量，则
$$\underset{K\to \infty }{\lim }{M}^K={\Gamma }_0^K{u}^{(0)}{u}^{(0)T}$$

证明：
设M的本征值分解为M $=U\Gamma U^T,$
有 $M^K=U\Gamma U^{T}U\Gamma U^T\dots U\Gamma U^T$
$由U{U}^T=U^{T}U=I$ 得, $M^K=U{\Gamma }^K{U}^T={\Gamma }_i^{K}U{\left(\frac{\Gamma }{{\Gamma }_i}\right)}^K{U}^T$
令 ${\Gamma }_{\mathrm{i}}={\Gamma }_0$
则${\lim }_{K\to \infty }{\left(\frac{\Gamma }{{\Gamma }_0}\right)}^K={\lim }_{K\to \infty }\left[\begin{array}{ccc}{\Gamma }_0/{\Gamma }_0& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\Gamma }_{D-1}/{\Gamma }_0\end{array}\right]\ast \ast \mathrm{K}=\mathrm{diag}([10$
得 ${\lim }_{k\to \infty }{\mathrm{M}}^{\mathrm{x}}={\Gamma }_0^{\mathrm{z}}\mathrm{U}\left[\begin{array}{ccc}1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\end{array}\right]{\mathrm{U}}^{\mathrm{T}}=\mathrm{U}\left[\begin{array}{lll}1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\end{array}\right]\left[\begin{array}{ccc}1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\end{array}\right]{\mathrm{U}}^{\mathrm{T}}={\Gamma }_0^{\mathrm{K}}{\mathrm{u}}^{(0)}{\mathrm{u}}^{(0)T}$
证毕
最大本征值问题的幂级数求解法的代码实现：

#使用scipy中的eigs求最大几个本征值和本征向量
import numpy as np
import scipy.sparse.linalg as la
import copy

dim=4
M=np.random.randn(dim,dim)#随机生成4×4的张量
M=M+M.T     
lm1,v1=la.eigs(M,k=1,which='LM')#求最大的本征值和本征向量
print(lm1)
print(M)

#最大本征值问题的幂级数求解法：
def eig0(mat,it_time=1000,tol=1e-15):
    v1=np.random.randn(mat.shape[0],)
    v0=copy.deepcopy(v1)
    lm=1
    for n in range(it_time):
        v1=mat.dot(v0)
        lm=np.linalg.norm(v1)#求本征值
        v1/=lm      #归一化
        #判断是否收敛
        conv=np.linalg.norm(v1-v0)
        if conv<tol:
            break
        else:
            v0=copy.deepcopy(v1)
        return lm,v1
        
lm2,v2=eig0(M)
print(lm2)
print(v2.reshape(-1,))

2. 奇异值分解与最优低秩近似问题

注意这个很重要，后面会有很多很多和这个有关的知识点。

奇异值分解（SVD）

奇异值分解（singular value decomposition）：给定D × D’的矩阵M，有
$$M=U\Lambda V^{†}$$

其中 $U$ 与V每一列分别被称为 $M$ 的左、右奇异向量，且满足正交归一性
$$U{U}^{†}=I,V{V}^{†}=I$$

$\Lambda$ 为非负定实对角矩阵，称为奇异谱, 其元素称为奇异值。矩阵的非零奇异值个数定义为矩阵的秩。类似于本征值分解，但是进行奇异值分解的矩阵可以不是方阵。如图所示：

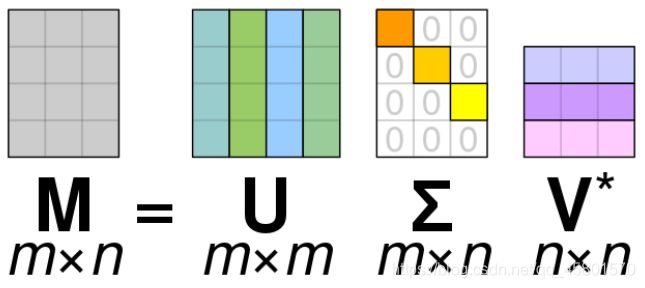
矩阵的低秩近似问题

给定 $D\times D^{\prime }$ 的矩阵M，设其秩为 $R$ 求解秩为 $R^{\prime }$ 的矩阵 $M^{\prime }$ 有 $R>R^{\prime }>0$ 且极小化二矩阵间的范数
$$\epsilon =||M-M^{\prime }||=\sqrt{\sum _{ij}{\left(M_{ij}-M_{ij}^{\prime }\right)}^2\sim \Vert {\Lambda }_{R^{\prime }:R-1}\Vert }(\text{ 裁剪误差 })$$

低秩近似问题的最优解为:
$$M^{\prime }=U\left[:,0:R^{\prime }\right]\wedge \left[0:R^{\prime },0:R^{\prime }\right]V{\left[:,0:R^{\prime }\right]}^{†}$$

代码实现：

import numpy as np
import matplotlib.image as pimg
import matplotlib.pyplot as plt

img=pimg.imread('C:/Users/86177/Pictures/Saved Pictures/ice.jpg')#导入图片
img=np.sum(img,axis=2) /3     #设置为灰度图片
print('shape of the image data = '+str(img.shape))
plt.imshow(img)
plt.show()

import scipy.sparse.linalg as la
#进行图片SVD分解
def img_compress(img,k):
    u,lm,v=la.svds(img,k=k)
    img1=u.dot(np.diag(lm)).dot(v)
    num_para=2*k*u.shape[0]
    #print(num_para)
    return img1,num_para
for k in range(10,100,40):
    img1,num_para=img_compress(img,k)
    plt.imshow(img1)
    plt.show()
    #进行奇异值分解后的相对误差
    print('error = '+str(np.linalg.norm(img-img1)/np.linalg.norm(img)))
    print('k = ',k)

由图可以看出当特征值取10个时图片很模糊，此时裁剪误差约13.9%；当特征值取50个时图片肉眼可见整理构图元素，此时裁剪误差约5.2%；当特征值取90个时图片很清晰，此时裁剪误差约3.2%，此时误差已经很小并且图片清晰度很高。可以采用此算法进行图片压缩从而减少所占存储空间。

高阶奇异值分解

高阶奇异值分解（简称HOSVD），又称Tucker分解
$$T_{abc}=\sum _{ijk}{G}_{ijk}{U}_{ai}{V}_{bj}{W}_{ck}$$

变换矩阵满足正交性
$$U{U}^T=V{V}^T=W{W}^T=I$$

张量G被称为核张量。定义G的键约化矩阵，以指标$i$为例，其键约化矩阵定义为：
$$J_{i{i}^{{}^{\prime }}}=\sum _{jk}{G}_{ijk}{G}_{i^{{}^{\prime }}jk}$$

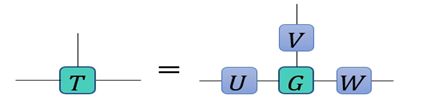
高阶奇异值分解算法
a.计算各指标的键约化矩阵（相同的指标进行缩并处理）：
$$\begin{array}{rl}{I}_{a{a}^{\prime }}& =\sum _{jk}{T}_{abc}{T}_{a^{\prime }bc}\\ J_{b{b}^{\prime }}& =\sum _{ik}{T}_{abc}{T}_{a{b}^{\prime }c}\\ K_{c{c}^{\prime }}& =\sum _{ij}{T}_{abc}{T}_{ab{c}^{\prime }}\end{array}$$

b.计算每个键约化矩阵的本征值分解：
$$I=U\Omega U^T$$

$$J=V\prod V^T$$

$$K=W{\rm Y}{W}^T$$

c.计算核张量：
$$G_{ijk}=\sum _{abc}{T}_{abc}{U}_{ai}{V}_{bj}{W}_{ck}$$

最终得到高阶奇异值分解：
$$T_{abc}=\sum _{ijk}{G}_{ijk}{U}_{ai}{V}_{bj}{W}_{ck}$$

有没有感觉奇异值分解也不是很难呢？

本人资质愚钝，我刚开始其实也是学了大概1 or 2个月才弄明白，如果没有懂，可以多查查资料或者欢迎评论区见。反正每天多思考，久而久之不懂的地方自然也就明白了。

2. 多线性代数中的张量单秩问题

记第n个左、右 奇异向量分别为u ${}^{(n)}$ 和 $v^{(n)}$ 证明如下等式：
$$\begin{array}{l}{\sum }_a{u}_a^{(n)}{M}_{ab}={\Lambda }^{(n)}{v}_b^{(n)}\\ {\sum }_b{M}_{ab}{v}_b^{(n)}={\Lambda }^{(n)}{u}_a^{(n)}\end{array}$$

其中， ${\Lambda }^{(n)}$ 为第n个奇异值, \quad 且有
$${\Lambda }^{(n)}=\sum _{ab}{u}_a^{(n)}{M}_{ab}{v}_b^{(n)}$$

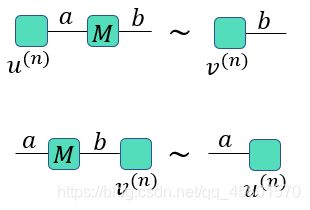计算最大奇异值及奇异向量的迭代算法（和矩阵的幂级数算法有点类似，不懂可以往前再看看哦！）:
（a）随机初始化归一向量u和v;
（b) 利用第一个式子，计算u和M的收缩并归一化，更新v，归一化因子记为 $\Lambda$
（c）利用第二个式子，计算v和M的收缩并归一化，更新u, 归一化因子记为 $\Lambda$
（d）如果u和v（以及 $\Lambda$ ) 收剑，则返回u、v和$\Lambda$; 否则，返回执行步骤
（b）最后我们会发现u和v刚好对应于M最大左、右奇异向量， 对应最大的奇异值。
将上述自洽方程组推广到高阶张量，得到如下自洽方程组（以三阶张量为例）：
$$\sum _{ab}{T}_{abc}{u}_a{v}_b=\Lambda w_c$$

$$\sum _{ac}{T}_{abc}{u}_a{w}_c=\Lambda v_b$$

$$\sum _{bc}{T}_{abc}{v}_b{w}_c=\Lambda u_a$$

u、v和w为归一化向量，方程组成立时满足：
$$\Lambda =\sum _{abc}{T}_{abc}{u}_a{v}_b{w}_c$$

其被称为rank-1分解，迭代求解的方法与二阶张量相同。

我学习张量有关的知识也不是很久，有很多东西也不懂。我是一只正在不断学习、希望早日成为小白的小小白，这是我第一次写博客，有什么错误欢迎大家批评指正，喜欢的请点个赞哦！