一个隐马尔科夫模型的应用实例:中文分词
什么问题用HMM解决
现实生活中有这样一类随机现象,在已知现在情况的条件下,未来时刻的情况只与现在有关,而与遥远的过去并无直接关系。
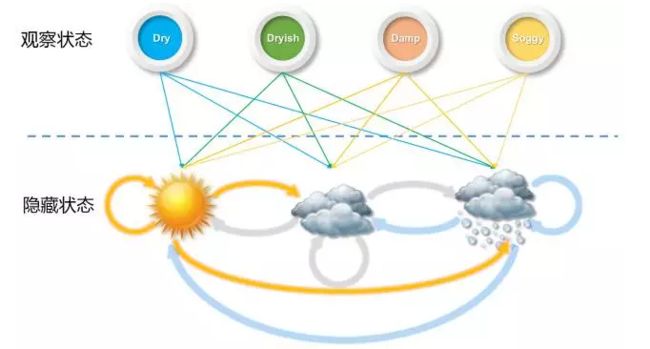
比如天气预测,如果我们知道“晴天,多云,雨天”之间的转换概率,那么如果今天是晴天,我们就可以推断出明天是各种天气的概率,接着后天的天气可以由明天的进行计算。这类问题可以用 Markov 模型来描述。
进一步,如果我们并不知道今天的天气属于什么状况,我们只知道今明后三天的水藻的干燥湿润状态,因为水藻的状态和天气有关,我们想要通过水藻来推测这三天的真正的天气会是什么,这个时候就用 Hidden Markov 模型来描述。
HMM 模型的本质是从观察的参数中获取隐含的参数信息,并且前后之间的特征会存在部分的依赖影响。
我们从如何进行中文分词的角度来理解HMM
根据可观察状态的序列找到一个最可能的隐藏状态序列
中文分词,就是给一个汉语句子作为输入,以“BEMS”组成的序列串作为输出,然后再进行切词,进而得到输入句子的划分。其中,B代表该字是词语中的起始字,M代表是词语中的中间字,E代表是词语中的结束字,S则代表是单字成词。
例如:给个句子
小明硕士毕业于中国科学院计算所得到BEMS组成的序列为
BEBEBMEBEBMEBES因为句尾只可能是E或者S,所以得到切词方式为
BE/BE/BME/BE/BME/BE/S进而得到中文句子的切词方式为
小明/硕士/毕业于/中国/科学院/计算/所这是个HMM问题,因为你想要得到的是每个字的位置,但是看到的只是这些汉字,需要通过汉字来推出每个字在词语中的位置,并且每个字属于什么状态还和它之前的字有关。
此时,我们需要根据可观察状态的序列找到一个最可能的隐藏状态序列。
五元组,三类问题,两个假设
五元组
通过上面的例子,我们可以知道 HMM 有以下5个要素。
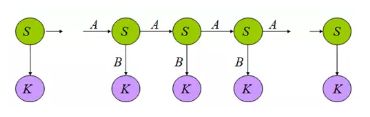
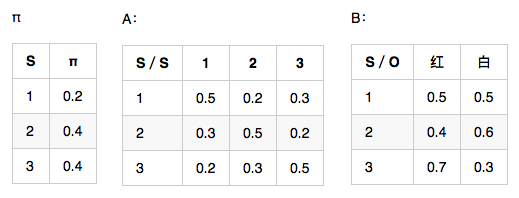
观测序列-O:小明硕士毕业于中国科学院计算所
状态序列-S:BEBEBMEBEBMEBES
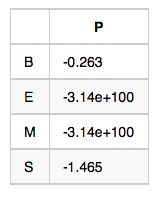
初始状态概率向量-π:句子的第一个字属于{B,E,M,S}这四种状态的概率
状态转移概率矩阵-A:如果前一个字位置是B,那么后一个字位置为BEMS的概率各是多少
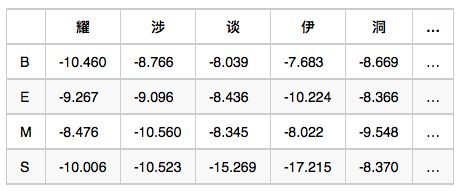
观测概率矩阵-B:在状态B的条件下,观察值为耀的概率,取对数后是-10.460
备注:示例数值是对概率值取对数之后的结果,为了将概率相乘的计算变成对数相加,其中-3.14e+100作为负无穷,也就是对应的概率值是0
三类问题
当通过五元组中某些已知条件来求未知时,就得到HMM的三类问题:
- 似然度问题:参数(O,π,A,B)已知的情况下,求(π,A,B)下观测序列O出现的概率。(Forward-backward算法)
- 解码问题:参数(O,π,A,B)已知的情况下,求解状态值序列S。(viterbi算法)
- 学习问题:参数(O)已知的情况下,求解(π,A,B)。(Baum-Welch算法)
中文分词这个例子属于第二个问题,即解码问题。
我们希望找到 s_1,s_2,s_3,… 使 P (s_1,s_2,s_3,…|o_1,o_2,o_3….) 达到最大。
意思是,当我们观测到语音信号 o_1,o_2,o_3,… 时,我们要根据这组信号推测出发送的句子 s_1,s_2,s_3,….,显然,我们应该在所有可能的句子中找最有可能性的一个。
两个假设
利用贝叶斯公式得到:
这里需要用到两个假设来进一步简化上述公式
有限历史性假设: si 只由 si-1 决定
独立输出假设:第 i 时刻的接收信号 oi 只由发送信号 si 决定
有了上面的假设,就可以利用算法 Viterbi 找出目标概率的最大值。
Viterbi算法
根据动态规划原理,最优路径具有这样的特性:如果最优路径从结点 i_{t}^ 到终点 i_{T}^,那么这两点之间的所有可能的部分路径必须是最优的。
依据这一原理,我们只需从时刻 t=1 开始,递推地计算在时刻 t 状态为 i 的各条部分路径的最大概率,直至得到时刻 t=T 状态为 i 的各条路径的最大概率 P^,最优路径的终结点 i_{T}^ 也同时得到。之后,为了找出最优路径的各个结点,从终结点 i_{T}^ 开始,由后向前逐步求得结点 i_{T-1}^…,i_{1}^,进而得到最优路径 I^=i_{1}^…,i_{T}^,这就是维特比算法.
举个栗子:
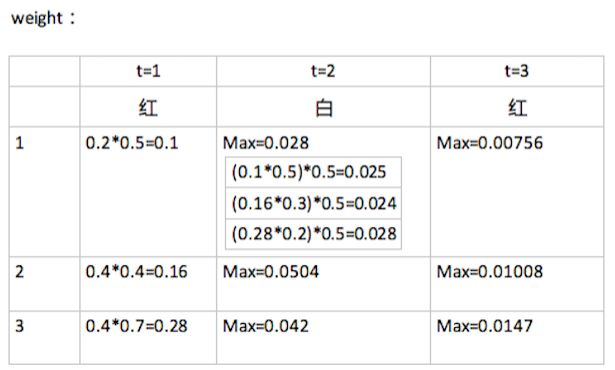
观测序列 O=(红,白,红),想要求状态序列S。
需要定义两个变量:
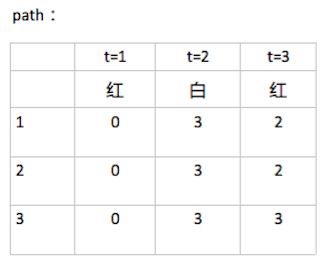
- weight[3][3],行3是状态数(1,2,3),列3是观察值个数(红,白,红)。意思是,在时刻 t 状态为 i 的所有单个路径中的概率最大值。
- path[3][3],意思是,在时刻 t 状态为 i 的所有单个路径中概率最大的那条路径,它的第 t-1 个结点是什么。比如 path[0][2]=1, 则代表 weight[0][2] 取到最大时,前一个时刻的状态是 1.
1.初始化
t=1 时的红,分别是在状态 1,2,3 的条件下观察得来的概率计算如下:
此时 path 的第一列全是 0.
2.递归
t=2 时的白,如果此时是在 1 的条件下观察得来的话,先计算此时状态最可能是由前一时刻的哪个状态转换而来的,取这个最大值,再乘以 1 条件下观测到 白 的概率,同时记录 path矩阵:如下图 weight[0][1]=0.028,此值来源于前一时刻状态是3,所以,
3.终止
在 t=3 时的最大概率 P^=0.0147,相应的最优路径的终点是 i_3^=3.
4.回溯
由最优路径的终点 3 开始,向前找到之前时刻的最优点:
- 在 t=2 时,因 i_3^=3,状态 3 的最大概率 P=0.0147,来源于状态 3,所以 i_2^=3.
- 在 t=1 时,因 i_2^=3,状态 3 的最大概率 P=0.042,来源于状态 3,所以 i_1^=3.
最后得到最优路径为 I^=(i_{1}^,i_{2}^,i_{3}^)=(3,3,3)
用Viterbi算法求解中文分词问题
根据上面讲的 HMM 和 Viterbi,接下来对中文分词这个问题,构造五元组并用算法进行求解。
InitStatus:π
TransProbMatrix:A
EmitProbMatrix:B
Viterbi求解
经过这个算法后,会得到两个矩阵 weight 和 path:
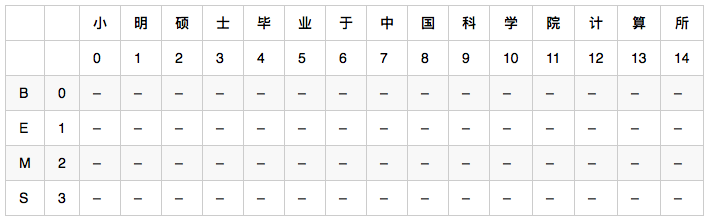
二维数组 weight[4][15],4是状态数(0:B,1:E,2:M,3:S),15是输入句子的字数。比如 weight[0][2] 代表 状态B的条件下,出现’硕’这个字的可能性。
二维数组 path[4][15],4是状态数(0:B,1:E,2:M,3:S),15是输入句子的字数。比如 path[0][2] 代表 weight[0][2]取到最大时,前一个字的状态,比如 path[0][2] = 1, 则代表 weight[0][2]取到最大时,前一个字(也就是明)的状态是E。记录前一个字的状态是为了使用viterbi算法计算完整个 weight[4][15] 之后,能对输入句子从右向左地回溯回来,找出对应的状态序列。
先对 weight 进行初始化,
使用 InitStatus 和 EmitProbMatrix 对 weight 二维数组进行初始化。
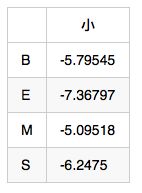
由 EmitProbMatrix 可以得出
所以可以初始化 weight[i][0] 的值如下:
注意上式计算的时候是相加而不是相乘,因为之前取过对数的原因。
然后遍历找到 weight 每项的最大值,同时记录了相应的 path
//遍历句子,下标i从1开始是因为刚才初始化的时候已经对0初始化结束了
for(size_t i = 1; i < 15; i++)
{
// 遍历可能的状态
for(size_t j = 0; j < 4; j++)
{
weight[j][i] = MIN_DOUBLE;
path[j][i] = -1;
//遍历前一个字可能的状态
for(size_t k = 0; k < 4; k++)
{
double tmp = weight[k][i-1] + _transProb[k][j] + _emitProb[j][sentence[i]];
if(tmp > weight[j][i]) // 找出最大的weight[j][i]值
{
weight[j][i] = tmp;
path[j][i] = k;
}
}
}
}如此遍历下来,weight[4][15] 和 path[4][15] 就都计算完毕。
确定边界条件和路径回溯
边界条件如下:
对于每个句子,最后一个字的状态只可能是 E 或者 S,不可能是 M 或者 B。
所以在本文的例子中我们只需要比较 weight[1(E)][14] 和 weight[3(S)][14] 的大小即可。
在本例中:
weight[1][14] = -102.492;
weight[3][14] = -101.632;
所以 S > E,也就是对于路径回溯的起点是 path[3][14]。
进行回溯,得到序列
SEBEMBEBEMBEBEB。再进行倒序,得到
BEBEBMEBEBMEBES接着进行切词得到
BE/BE/BME/BE/BME/BE/S最终就找到了分词的方式
小明/硕士/毕业于/中国/科学院/计算/所HMM还有哪些应用
HMM不只用于中文分词,如果把 S 换成句子,O 换成语音信号,就变成了语音识别问题,如果把 S 换成中文,O 换成英文,就变成了翻译问题,如果把 S 换成文字,O 换成图像,就变成了文字识别问题,此外还有词性标注等等问题。
对于上述每种问题,只要知道了五元组中的三个参数矩阵,就可以应用 Viterbi 算法得到结果。
原文链接:http://www.jianshu.com/p/f140c3a44ab6
著作权归作者所有,转载请联系作者获得授权,并标注“简书作者”。