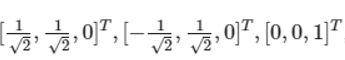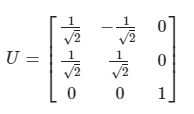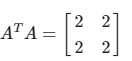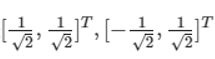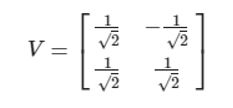基于张量网络的机器学习(三)
本次将继续学习张量分解的有关内容。
一.非负矩阵分解(Nonnegative Matrix Factorization)
1.非负矩阵分解
非负矩阵分解由Lee和Seung于1999年在自然杂志上提出,它使分解后的所有分量均为非负值,并且同时实现非线性的
维数约减。
先找到一个F维向量 ν \nu ν,然后对其进行N次观测从而得到N个向量排列而成的矩阵 V,其中 V=[ ν \nu ν1 ν \nu ν2 … ν \nu νN],然后分别找到基矩阵 W(F × \times ×K)和系数矩阵 H (K × \times ×N)使得满足下图式子:
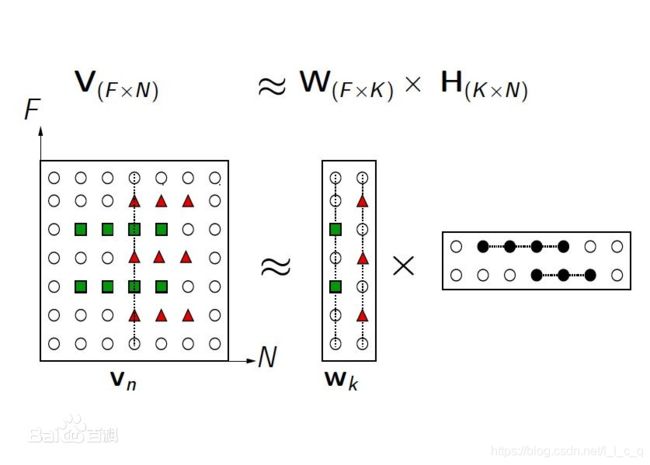
通过上图例子可以发现矩阵 V 和 W H 是近似,这是简单的矩阵乘法并满足一定的规律,找到了规律后你会发现的确是近似,所以用的约等于。
另外,如果矩阵 W 的基集过完备(矩阵秩小于列数量,这里的基集并不是值极大线性无关组),就会导致所谓数据的稀疏表示问题;由于在寻找基矩阵和系数矩阵时并不是确定其中一个就能确定另一个的,所以 非负矩阵分解是非线性的;为什么要分解成非负矩阵?因为负值元素在实际问题中基本没有多大意义;维数约减顾名思义是降维,但是降维是要尽量好地降维,尽量避免数据的丢失,如下:

由于所给数据点大致落在一个平面内,我们可以通过维数约减,将数据点基本映射在一个平面上,以便更好地理解这些数据(比如二维层面的某种相关性)。有时候,那些多余的数据是冗余的,去除这些数据就相当于去噪,还能减少存储空间。
再举个例子:
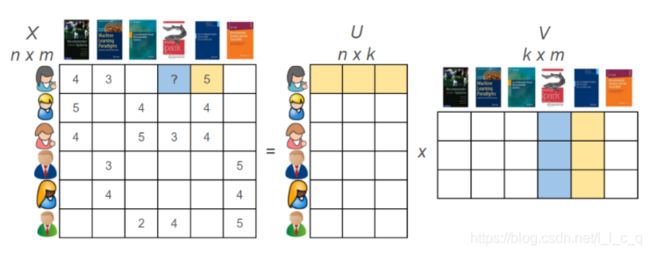
这是一个典型的不同用户对不同书籍进行评分的例子,当然上图是不完整的,所以图中左边的数据不用管。现在,我对这张图做点修改:

矩阵 U 里面的值是对A、B、C中某个要素的评分,同一个用户对每本书的每种要素评分都相同,但是每本书在每种要素上占的比例是不同的,并且我们要求评分和比例都非负,最后可以得到左边那个矩阵,通过这样一个矩阵得到的数据,我们可以把评分高的书籍推荐给新老用户。
2.求解
- 损失函数的定义
损失函数一种是通过欧几里得距离定义,一种是通过KL散度定义(相对熵),后者求解式子看着太复杂,所以只介绍欧几里得距离的损失函数,即:
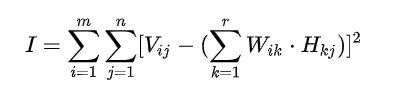
- 求解
先将非负矩阵分解问题转化成求解下列最小化问题:

定义损失函数:
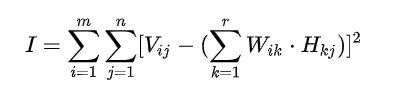
上面这个损失函数的值是矩阵(V-WH)中每个元素的和,然后求梯度:
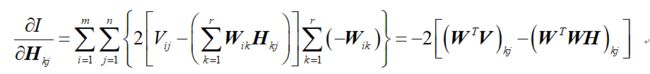
依照梯度下降法的思路,令:
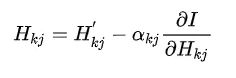
其中
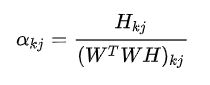
则

类似的:
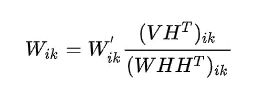
具体的推导过程和梯度下降法的思路这里不介绍,我会专门写一篇博客来介绍梯度下降法以及某些重要的算法。
3.面临的困难(K值选取的困难)
如下图:
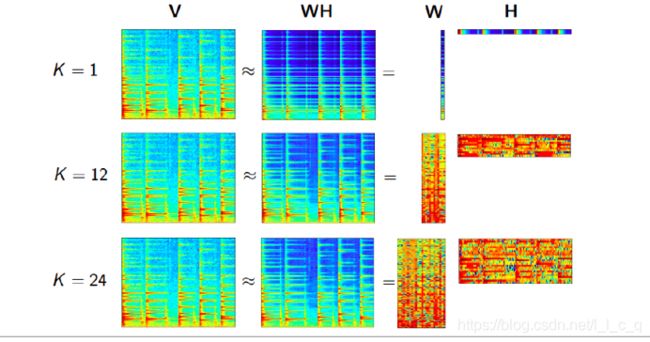
参数k根据上面举的例子可以理解为选取要素的数量,其中那个例子里面有三个要素,从而k=3,如果k越大,评分越准确,也就是损失值(损失函数的值,姑且叫做损失值)更小,但是更难得到,k越小也就可以类比得到,k更好的说法我认为是训练次数。
上图详细点说是在K不同时使用非负矩阵分解的结果,k越大,数据拟合的越好,但复杂度会更高(更难得到),所以常常需要找到一个平衡点去训练数据。
4.应用
NMF的广泛应用,源于其对事物的局部特性有很好的解释。
前面已经提到了两个应用,一个是用于推荐书,一个是处理声频,前者是文本聚类,后者是语音处理,除这两种以外,非负矩阵分解还可以用于图像分析(其实各种张量分解都是可以用于图像分析的,毕竟二维张量就可以表示灰度图像,三维张量可以表示彩色图像),人们还利用NMF算法,对卫星发回的图像进行处理,以自动辨别太空中的垃圾碎片。

二.奇异值分解
(一般)矩阵的奇异值分解(SVD)
1.奇异值分解
学过线性代数的一定学过特征分解,对于一个矩阵 A,通过对角化可以得到一个可逆矩阵和对角线上为均为特征值的对角矩阵,具体分类情况不再赘述。
特征分解是针对方阵的,奇异值分解是特征分解在任意矩阵上的推广,显然奇异值分解有者更广泛的作用。
对于一个m × \times ×n矩阵 A,这个矩阵可以定义在实数域也可以定义在复数域上,那么存在一个分解使得:
![]()
其中矩阵 U 为m阶幺正矩阵(酉矩阵),矩阵 V 为n阶幺正矩阵(酉矩阵), ∗ \ast ∗表示共轭转置, Σ \Sigma Σ为一个m × \times ×n奇异值矩阵,即除对角线上都为矩阵 A 的奇异值外,其他元素都为0,且 U 被称为左奇异矩阵, V 被称为右奇异矩阵,满足以下关系:
![]()
然后 Σ \Sigma Σ满足:

或:
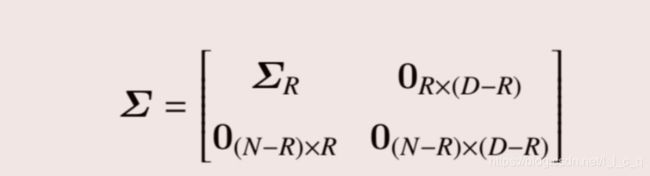
由奇异值分解定理还可以得到:
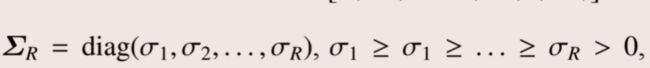
所以 Σ \Sigma Σ又是一个半正定的m × \times ×n奇异值矩阵, σ \sigma σR为奇异值。
2.求解
先举一个计算的例子,这个例子可以让你清晰地意识到如何通过数学计算出左奇异矩阵、右奇异矩阵和奇异值矩阵。
现在有一个矩阵:
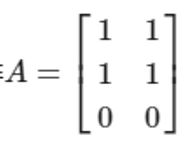
第一步:先计算左奇异矩阵 U :
第二步:然后再计算右奇异值矩阵 V :
第三步:最后计算奇异值矩阵(将第一步或者第二步得到特征值从大到小排列并开根号):

在现实生活中,奇异值的计算是一个难题,当矩阵的规模增长的时候,计算的复杂度呈3次方增长,这时就需要平行计算。
3.部分奇异值分解
由于一个矩阵的奇异值矩阵的前几个奇异值都比较大,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上,所以可以用前r个较大的奇异值来对原矩阵做近似,表达式如下:
![]()
因为r比较小,所以可以用更少的存储空间来表示矩阵 A 。
4.奇异值分解的性质
上面不等式右边的是一个2-范数, λ \lambda λmax是矩阵 (A-B) T (A-B) 的最大特征值。
- 奇异值的比例不变性:矩阵进行数乘变换,奇异值也成比例变化。
- 奇异值的旋转不变性:即若P是正交阵,PA 的奇异值与 A 的奇异值相同.。
- 容易得到矩阵 A 的秩为k(k<=r)的一个最佳逼近矩阵 B :
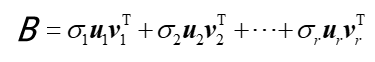
其中:

这样计算方法简单,但是通过迭代计算,计算复杂度较高。
5.主成分分析(PCA)
PCA的实现一般有两种,一种是通过特征值分解,另一种是通过奇异值分解,此处着重奇异值分解实现PCA。
主成分分析的实质是 降维 ,即用较少的变量来代替较多的变量,部分奇异值分解就体现了降维的思想,主成分分析可以处理多变量问题,减少分析问题的复杂性。
先看看将数据矩阵进行SVD分解后里面有关主成分分析的部分:
-首先是左奇异矩阵,左奇异矩阵里面的每个奇异值对应的列向量都是在列空间中主成分方向的正交分解,在奇异值最大的列向量这个方向上,数据差异体现的最明显。
- 然后是右奇异矩阵,与左奇异矩阵类似,右奇异矩阵里面的每个奇异值对应的行向量都是在行空间中主成分方向的正交分解,在奇异值最大的行向量这个方向上,数据差异体现的最明显。
- 最后是奇异值矩阵,奇异值越大,方差越大。
主成分分析需要找到主成分方向和主成分,主成分分析体现了基的变换,变换后的基要使得数据的方差最大,如果方差小反而很难体现数据之间的差异性,所以关键是要找到一组新的正交基,并满足一定的要求。
现在先找到一个基,在这个基(奇异值对应的奇异向量)下,方差最大,奇异值最大,接着再找基,在这个基下,方差和奇异值次大,依次类推。这里还遇到了一个问题,这组正交基取左奇异矩阵还是右奇异矩阵?答案是都可以,这也导致有两种主成分分析的方式,还有一点可以了解一下, 正交矩阵必可逆 ,所以奇异值分解的结果也是唯一的(唯一的左、右奇异矩阵和奇异值矩阵),无论按上面哪种方式进行主成分分析,相应的奇异向量都可以作为基,在由这组基生成的超空间下,各个基的代数和得到的向量就是这种PCA下的主成分方向,所以有两种主成分方向。
如果我们最多只能选n个正交基,那这就是最佳逼近;如果我们少选几个,这就是部分奇异值分解;只选几个关键的,这就很好地应用在某些领域了,比如图像压缩,曲线拟合(要相关性体现的较好)。
有时候也会说左奇异矩阵或者右奇异矩阵为某数据协方差矩阵的主成分方向,这个数据协方差矩阵就等于原始矩阵与其转置后的矩阵的乘积,它的迹即为方差和,也等于各个奇异值的平方和,再深入就会涉及更多的概念,所以到这就差不多了。
6.应用
首先给出关于矩阵应用的一些基本信息:

然后介绍一些关于奇异值分解的一些应用:
-
图像恢复:图像恢复实际上是一个矩阵填充的过程,矩阵填充是为了找到丢失的元素(或者说预测不知道的元素),通过低秩矩阵以提供较为良好的近似(前面的部分奇异值分解)

比较奇怪的是为什么最后一个条船是反着来的。

-
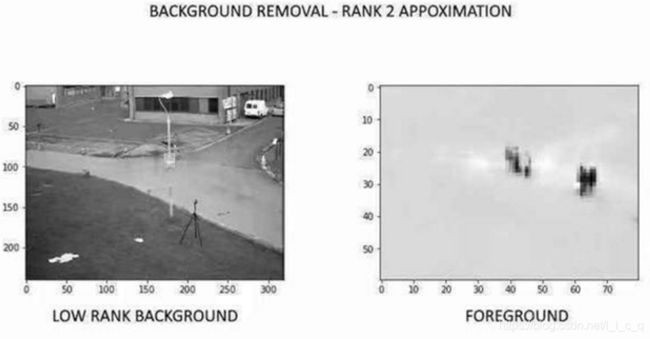
从视频中删除背景:从视频创建矩阵 M ,M 可以视为两个矩阵的和,一个表示前景,一个表示背景,一般情况我们想要前景(整张图里的某个要素,可以是一个人,一朵花,或者说整张图里“最靓的仔”’),显然前景信息更多,背景信息更少,所以我们对矩阵 M 做SVD的低秩近似得到的低秩矩阵就可以表示背景了,然后用矩阵 M 一减就能得到表示前景的矩阵了,如图展示了一个视频的一帧的低秩背景和前景:
三.Tucker分解
张量的模乘
张量 χ \chi χ的模乘是指张量 χ \chi χ与矩阵 U 的n模相乘,即:
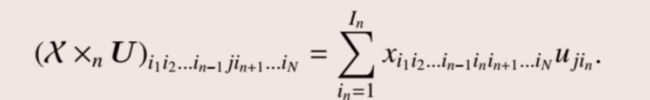
其中:

为了便于理解,给出下图:
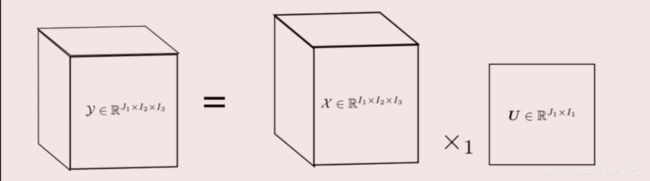
一个三阶张量与一个矩阵的n模相乘,实际上是将张量固定好I2、I3,然后一片一片地拿来与这个矩阵相乘。
所以与n个矩阵连续模乘即:
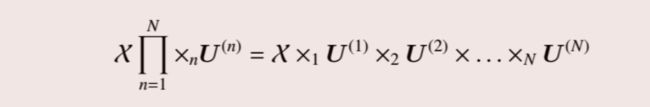
其中:
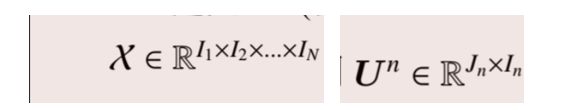
Tucker分解
张量的Tucker分解将M阶张量 χ \chi χ ∈ \in ∈RI1 × \times ×I2 × \times ×… × \times ×IN分解为一个核心张量 G \mathcal{G} G ∈ \in ∈RR1 × \times ×R2 × \times ×… × \times ×RN与正交矩阵模乘的形式,具体表现为:
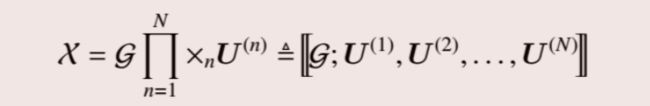
其中:
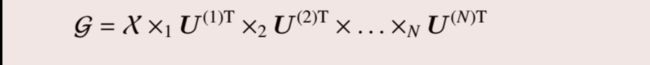
由于模乘的每个矩阵都是正交矩阵,很容易看出上面这个式子是对的。
再写成n模矩阵展开的形式:
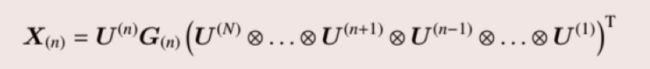
这里的Tucker分解能取等号取决于每个用来模乘的矩阵的列数是否是满的(最大的),一旦不是满的,此时的Tucker分解称为截断Tucker分解,且等号变为约等号,

Tucker分解是一种高阶的主成分分析,上面每一个正交矩阵可视为张量 χ \chi χ沿着相应模的主成分。
Tucker2和Tucker1
对于一个三阶张量,如果固定某一个正交矩阵为单位矩阵,则可称为Tucker2,如果固定两个正交矩阵为单位矩阵,则可称为Tucker1,此时退化为普通的PCA,具体的式子可以根据前面的内容进行推导。
求解
Tucker分解的求解依赖于HOOL算法,如果进一步简化,就依赖于HOSVD算法。
依然是将Tucker分解的问题转化为一个最优化问题:
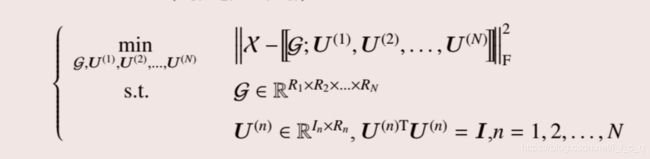
之后可以将第一个式子展开并对上面的最优化问题进行转化得到:
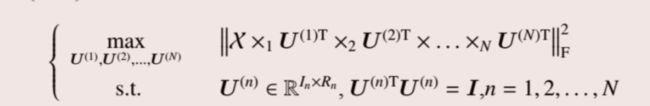
然后利用ALS算法得到子问题再进行迭代:
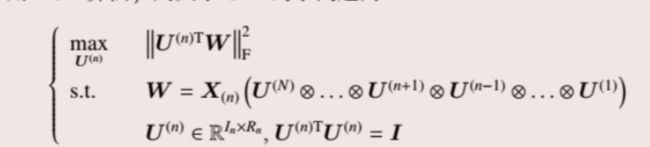
具体算法步骤如下:

如果进行简化,简化后的HOSVD算步骤如下:

HOSVD将一个张量分解为一个核心张量和n个正交矩阵的连续模乘,但是这n个正交矩阵是通过将张量n-mode矩阵化后再做SVD得来的左奇异矩阵。
还要注意的地方就是Rn为各个正交(因子)矩阵的列数。
应用
Tucker分解可用于化学分析、计量心理学、信号处理、机器视觉(面部、动作)、数据压缩、纹理生成、数据挖掘、环境和网络建模,这些应用了解即可。
四.其他矩阵分解
通过矩阵分解方法去求解线性方程组的优点是运算速度快,而且节省存储空间,以下介绍的矩阵分解不会过于深入。
1.LU分解
矩阵的 LU 分解是指将一个方阵 A 分解为一个下三角矩阵和一个上三角矩阵 U 的乘积,使用matlab有两种方式:
2.正交分解(QR)
矩阵的 QR 分解是指将一个矩阵 A 分解为一个正交矩阵 Q 和一个上三角矩阵 R 的乘积,其中Q是正交矩阵,且 QQ T= E ,故QR分解又称为正交分解,使用matlab也有两种方式:
3.Cholesky分解
Cholesky分解是指将一个对称正定矩阵 A 分解成一个下三角矩阵 R 和和其转置矩阵的乘积,使用matlab依旧有两种方式:
-
第一种:

产生一个上三角矩阵 R 使得 A = R T R ,而且还对矩阵 A 是不是正定矩阵以及得到的矩阵 R 是否正确进行了验证。 -
第二种


如果矩阵 A 是一个对称正定矩阵,则数p等于0,矩阵 A 不是一个对称正定矩阵,则数p为一个正数且不会显示错误信息。