对PBFT算法的一点理解
文章目录
- 背景
- 前言
- 算法
- 总览
- 三个阶段
- 垃圾回收
- 视图更换
- 其他
- 参考
导师让看一下SBFT,刚看了一点发现需要先理解PBFT,于是先去看了PBFT,太菜了看了好久才大概弄明白什么情况,这里简单记录一下自己的理解。
背景
背景部分就不细说了,该算法的提出主要是为了解决拜占庭问题(Byzantine Fault Tolerance),P代表Practical,实用的意思,该算法将原先的复杂度为指数的一个算法进行了取舍与优化,达到 O ( N 2 ) O(N^2) O(N2)的复杂度,可以在实际中工程中使用。
前言
以往的BFT算法大部分都基于同步系统(synchronous system),也就是系统可以在已知的有限时间内完成计算和网络传输的任务,异步系统(Asynchronous System)是指计算和网络传输的时间可能无限长。而现实中的系统一般是半同步系统,也就是计算和网络传输可以在有限时间内完成,但这个时间是无法预知的。
如果系统中存在 F F F个恶意节点,那么PBFT算法总共需要 N = 3 F + 1 N=3F+1 N=3F+1个节点来保证系统的liveness和safety,也就是说若系统有 N N N个节点,则该系统可以容忍 ⌊ N − 1 3 ⌋ \lfloor{\frac{N-1}{3}}\rfloor ⌊3N−1⌋个恶意节点。
节点可以分为三类。一直正常工作的节点,二是出现错误的节点(比如延迟、宕机),三是恶意节点(故意做坏事)。
safety:是指满足linearizability,也就是像中心化系统一样,一次只进行一个原子操作。(大概就是说所有节点保持一致?)
liveness:是指client发出的request都会得到reply。
为什么容忍 F F F个节点错误需要 3 F + 1 3F+1 3F+1个节点?
因为 F F F个恶意节点可能故意不回复,因此当收到 N − F N-F N−F个回应时要做出决定,但是我们知道所有的节点都可能会出现延迟或者宕机的情况,还没回复的 F F F个节点也可能存在正常的节点(甚至全都是正常的节点),回复的 N − F N-F N−F个节点中可能也存在恶意节点(甚至 F F F个恶意节点都进行了错误的回复),为了达成共识,我们需要保证已经回复的节点中正常节点的数量大于恶意节点的数量,也就是 N − F − F > F N-F-F>F N−F−F>F(第一个 F F F是指减去没有回复的节点,第二个 F F F是指减去可能存在的恶意节点,右边的 F F F指恶意节点),也就是 N > 3 F N>3F N>3F,即 N ≥ 3 F + 1 N\ge3F+1 N≥3F+1.
算法
总览
PBFT算法是状态机复制(state machine replication)的一种形式,将服务建模成状态机在分布式系统的不同节点间复制。这里需要理解一个视图(View)的概念:client将request发给一个主节点(primary),然后主节点将request多播到其他节点(backups),当主节点出错或成为恶意节点时,就需要进行视图更换(view change),也就是选择(轮换法)下一个backup作为主节点,共识过程进入下一个view。
总体算法流程如下:
- client向
primary发起request primary将request多播到backups- 节点发送reply给client
- client等待 F + 1 F+1 F+1个结果相同的reply作为最终结果
该算法成立的两个前提条件:
- 节点的行为必须是确定的,也就是在相同的状态下输入相同的参数,必须返回相同的结果
- 每个节点都必须从同一个状态开始
三个阶段
共识机制主要分三个阶段:pre-prepare, prepare,commit. 如下图,C是client,0号节点是primary,其他节点是backups,3号节点是拜占庭节点。
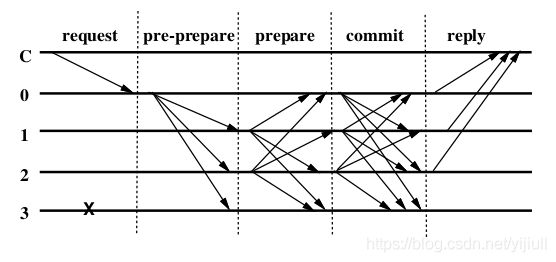
- request阶段:client发送 ⟨ R E Q U E S T , o , t , c ⟩ σ i \left\langle REQUEST,o,t,c \right\rangle_{\sigma_i} ⟨REQUEST,o,t,c⟩σi给
primary,其中t是时间戳,o表示操作,c是这个client - pre-prepare阶段:
primary赋予收到的request一个编号 n n n,然后将消息 ⟨ ⟨ P R E − P R E P A R E , v , n , d ⟩ σ p , m ⟩ \left\langle \left\langle PRE-PREPARE, v, n, d \right\rangle_{\sigma_p} , m\right\rangle ⟨⟨PRE−PREPARE,v,n,d⟩σp,m⟩转发给backups,如果满足条件backup就接受这条消息(条件一般都是在同一个视图中,签名有效,n在高低水位之间等,具体可以参考其他博客或者看论文,这里不细说) - prepare阶段:如果
backup接受了primary发来的 ⟨ ⟨ P R E − P R E P A R E , v , n , d ⟩ σ p , m ⟩ \left\langle \left\langle PRE-PREPARE, v, n, d \right\rangle_{\sigma_p} , m\right\rangle ⟨⟨PRE−PREPARE,v,n,d⟩σp,m⟩消息,那么就进入prepare阶段,并多播 ⟨ P R E P A R E , v , n , d , i ⟩ σ i \left\langle PREPARE, v, n, d, i \right\rangle_{\sigma_i} ⟨PREPARE,v,n,d,i⟩σi消息给其他节点,同时将消息记录到log中。同时节点接受满足条件的其他节点发来的 ⟨ P R E P A R E , v , n , d , i ⟩ σ i \left\langle PREPARE, v, n, d, i \right\rangle_{\sigma_i} ⟨PREPARE,v,n,d,i⟩σi消息,如果接受的数量达到 2 F 2F 2F个,那么准备阶段就完成了, p r e p a r e d ( m , v , n , i ) prepared(m,v,n,i) prepared(m,v,n,i)为真,就可以进入下一阶段了 - commit阶段: 已经 p r e p a r e d ( m , v , n , i ) prepared(m,v,n,i) prepared(m,v,n,i)的节点可以多播 ⟨ C O M M I T , v , n , D ( m ) , i ⟩ σ i \left\langle COMMIT, v, n, D(m), i \right\rangle_{\sigma_i} ⟨COMMIT,v,n,D(m),i⟩σi给其他节点(包括自己),进入commit阶段,并接受其他节点发来的满足条件的 ⟨ C O M M I T , v , n , D ( m ) , i ⟩ σ i \left\langle COMMIT, v, n, D(m), i \right\rangle_{\sigma_i} ⟨COMMIT,v,n,D(m),i⟩σi消息,同时将该消息插入log中。
- 如果节点 i i i处于 p r e p a r e d ( m , v , n , i ) prepared(m,v,n,i) prepared(m,v,n,i)状态并收到了 2 F + 1 2F+1 2F+1个 ⟨ C O M M I T , v , n , D ( m ) , i ⟩ σ i \left\langle COMMIT, v, n, D(m), i \right\rangle_{\sigma_i} ⟨COMMIT,v,n,D(m),i⟩σi消息,那么就认为达到了 c o m m i t e d − l o c a l ( m , v , n , i ) commited-local(m,v,n,i) commited−local(m,v,n,i)状态,然后就可以执行client的请求并返回 ⟨ R E P L Y , v , t , c , i , r ⟩ σ i \left\langle REPLY, v,t,c,i,r \right\rangle_{\sigma_i} ⟨REPLY,v,t,c,i,r⟩σi给client。
- 当client收到 F + 1 F+1 F+1个相同的 ⟨ R E P L Y , v , t , c , i , r ⟩ σ i \left\langle REPLY, v,t,c,i,r \right\rangle_{\sigma_i} ⟨REPLY,v,t,c,i,r⟩σi时(
t和r相同),就完成了共识。
垃圾回收
根据前面的算法部分可以发现,我们需要不断地往log中插入消息,view change(后面会讲到)时恢复需要用到。于是log很快就会变得很占内存,需要有一种方式清理掉无用的log。当某一request已经被 F + 1 F+1 F+1个正常节点执行完毕后,并当view change时可以向其他节点证明当前状态的正确性,与该request相关的message就可以删除了。
每执行一个request就产生一次证明效率过于低下,论文中是每处理一定的request后产生一次证明。也就是当request的序号 n % C ( 某 一 定 值 ) = = 0 n \% C(某一定值) == 0 n%C(某一定值)==0时,产生一个checkpoint,节点 i i i多播 ⟨ C H E C K P O I N T , n , d , i ⟩ σ i \left\langle CHECKPOINT, n,d,i \right\rangle_{\sigma_i} ⟨CHECKPOINT,n,d,i⟩σi给其他节点。当节点接受 2 F + 1 2F+1 2F+1个 ⟨ C H E C K P O I N T , n , d , i ⟩ σ i \left\langle CHECKPOINT, n,d,i \right\rangle_{\sigma_i} ⟨CHECKPOINT,n,d,i⟩σi消息时,该checkpoint变为stable checkpoint,也就是者 2 F + 1 2F+1 2F+1个节点可以证明该状态的正确性,同时可以删除序号 ≤ n \le n ≤n的消息相关的log信息和checkpoint信息。
高效地计算证明用到了incremental cryptography,这里暂时不作说明。
同时这里也说明了前面提到的高低水位,低水位就是stable checkpoint的序号 n n n,高水位是stable checkpoint的序号 n + K n+K n+K,其中 K K K是定值,一般是 C C C的整数倍。
视图更换
如果primary是恶意节点,该如何处理?View change就是为了处理这种情况。
每个backup收到request时都会启动一个计时器,如果超时之后仍没有执行该request,那么就认为primary出了问题,就会发起视图更换,多播 ⟨ V I E W − C H A N G E , v + 1 , n , C , P , i ⟩ σ i \left\langle VIEW-CHANGE, v+1, n, C, P, i \right\rangle_{\sigma_i} ⟨VIEW−CHANGE,v+1,n,C,P,i⟩σi消息给其他节点。这里的 n n n是该节点的stable checkpoint对应的序号, C C C是 2 F + 1 2F+1 2F+1个有效的checkpoint消息(证明该stable checkpoint正确性), P P P是一个集合,如果消息m在当前backup达到prepared状态并且序号大于 n n n,那么与该消息相关的pre-prepare和prepare消息会放到集合 P m P_m Pm中,将 P m P_m Pm放到 P P P中。
当新view的primary接受 2 F 2F 2F个有效的 ⟨ V I E W − C H A N G E , v + 1 , n , C , P , i ⟩ σ i \left\langle VIEW-CHANGE, v+1, n, C, P, i \right\rangle_{\sigma_i} ⟨VIEW−CHANGE,v+1,n,C,P,i⟩σi消息时,就多播 ⟨ B E W − V I E W , v + 1 , V , O ⟩ σ p \left\langle BEW-VIEW, v+1, V, O \right\rangle_{\sigma_p} ⟨BEW−VIEW,v+1,V,O⟩σp给其他节点,其中 V V V是该primary收到的 ⟨ V I E W − C H A N G E , v + 1 , n , C , P , i ⟩ σ i \left\langle VIEW-CHANGE, v+1, n, C, P, i \right\rangle_{\sigma_i} ⟨VIEW−CHANGE,v+1,n,C,P,i⟩σi消息和自己发出的 ⟨ V I E W − C H A N G E , v + 1 , n , C , P , i ⟩ σ i \left\langle VIEW-CHANGE, v+1, n, C, P, i \right\rangle_{\sigma_i} ⟨VIEW−CHANGE,v+1,n,C,P,i⟩σi的集合, O O O是一个pre-prepare消息的集合, O O O的具体计算方式如下:
primary确定序号的范围,集合 V V V中的latest stable checkpoint对应的序号作为min-s,集合 V V V中的prepare message消息对应的最大的序号作为max-s.primary对于在min-s和max-s之间的每一个序号 n n n为新的视图构造pre-prepare消息,这里分为了两种情况:- 如果在view-change消息的集合 P P P中至少存在一个集合的序号是 n n n,那么就构造 ⟨ P R E − P R E P A R E , v + 1 , n , d ⟩ σ p \left\langle PRE-PREPARE, v+1, n, d \right\rangle_{\sigma_p} ⟨PRE−PREPARE,v+1,n,d⟩σp消息,这里的 d d d是集合 V V V中view number最大的序号 n n n对应的pre-prepare消息中的签名(有点绕,不是很懂)。
- 否则构造 ⟨ P R E − P R E P A R E , v + 1 , n , d n u l l ⟩ σ p \left\langle PRE-PREPARE, v+1, n, d^{null} \right\rangle_{\sigma_p} ⟨PRE−PREPARE,v+1,n,dnull⟩σp消息,其实就是无意义的消息,不执行操作。
primary将集合 O O O中的消息记录到log中,同时可能要更新自己的stable checkpoint,然后正式进入新的view。
backup接受有效的视图更换消息,然后验证O的正确性(执行与primary相似的运算),将消息加入log,就可以根据集合 O O O中的pre-prepare消息产生prepare消息进行多播了,进入新的view。
可以看出,虽然redo了序号在min-s和max-s之间的request,但是并没有re-execute这些request(???),(使用了他们上一次发给client时存储下来的信息)。
其他
关于正确性和优化这里不做说明,请参考原论文和相关博客。
参考
- 同步系统&&异步系统:https://blog.csdn.net/TurkeyCock/article/details/81781082
- 关于Quorum: https://blog.csdn.net/jason_cuijiahui/article/details/79613633
- https://blog.csdn.net/kojhliang/article/details/80270223
- https://blog.csdn.net/jerry81333/article/details/74303194
- https://www.jianshu.com/p/78e2b3d3af62
- https://www.cnblogs.com/gexin/p/10242161.html
- https://www.jianshu.com/p/fb5edf031afd
- 数学公式latex:https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference
上面的链接里有些存在部分小错误,自行分辨。