中文分词之基础算法-隐马和维特比算法
隐马尔可夫模型（HMM）可以用五个元素来描述，包括2个状态集合和3个概率矩阵：
1. 隐含状态 S
这些状态之间满足马尔可夫性质，是马尔可夫模型中实际所隐含的状态。这些状态通常无法通过直接观测而得到。（例如S1、S2、S3等等)
2. 可观测状态 O
在模型中与隐含状态相关联，可通过直接观测而得到。(例如O1、O2、O3等等，可观测状态的数目不一定要和隐含状态的数目一致。）
3. 初始状态概率矩阵 π
表示隐含状态在初始时刻t=1的概率矩阵，(例如t=1时，P(S1)=p1、P(S2)=P2、P(S3)=p3，则初始状态概率矩阵 π=[ p1 p2 p3 ].
4. 隐含状态转移概率矩阵 A。
描述了HMM模型中各个状态之间的转移概率。
其中Aij = P( Sj | Si ),1≤i,,j≤N.
表示在 t 时刻、状态为 Si 的条件下，在 t+1 时刻状态是 Sj 的概率。
5. 观测状态转移概率矩阵 B （英文名为Confusion Matrix，直译为混淆矩阵不太易于从字面理解）。
令N代表隐含状态数目，M代表可观测状态数目，则：
Bij = P( Oi | Sj ), 1≤i≤M,1≤j≤N.
表示在 t 时刻、隐含状态是 Sj 条件下，观察状态为 Oi 的概率。
总结：一般的，可以用λ=(A,B,π)三元组来简洁的表示一个隐马尔可夫模型。隐马尔可夫模型实际上是标准马尔可夫模型的扩展，添加了可观测状态集合和这些状态与隐含状态之间的概率关系。
基本问题
1. 评估问题。
给定观测序列 O=O1O2O3…Ot和模型参数λ=(A,B,π)，怎样有效计算某一观测序列的概率，进而可对该HMM做出相关评估。例如，已有一些模型参数各异的HMM，给定观测序列O=O1O2O3…Ot，我们想知道哪个HMM模型最可能生成该观测序列。通常我们利用forward算法分别计算每个HMM产生给定观测序列O的概率，然后从中选出最优的HMM模型。
这类评估的问题的一个经典例子是语音识别。在描述语言识别的隐马尔科夫模型中，每个单词生成一个对应的HMM，每个观测序列由一个单词的语音构成，单词的识别是通过评估进而选出最有可能产生观测序列所代表的读音的HMM而实现的。
2.解码问题
给定观测序列 O=O1O2O3…Ot 和模型参数λ=(A,B,π)，怎样寻找某种意义上最优的隐状态序列。在这类问题中，我们感兴趣的是马尔科夫模型中隐含状态，这些状态不能直接观测但却更具有价值，通常利用Viterbi算法来寻找。
这类问题的一个实际例子是中文分词，即把一个句子如何划分其构成才合适。例如，句子“发展中国家”是划分成“发展-中-国家”，还是“发展-中国-家”。这个问题可以用隐马尔科夫模型来解决。句子的分词方法可以看成是隐含状态，而句子则可以看成是给定的可观测状态，从而通过建HMM来寻找出最可能正确的分词方法。
3. 学习问题。
即HMM的模型参数λ=(A,B,π)未知，如何调整这些参数以使观测序列O=O1O2O3…Ot的概率尽可能的大。通常使用Baum-Welch算法以及Reversed Viterbi算法解决。
怎样调整模型参数λ=(A,B,π)，使观测序列 O=O1O2O3…Ot的概率最大？
中文分词涉及到的一般是解码问题
解码问题的求解算法：
对于篱笆网络的维特比算法
维特比算法利用动态规划思想求解概率最大路径（可理解为求图最短路径问题）， 其时间复杂度为O（N*L*L），其中N为观察者序列长度，L为隐含状态大小。该算法的核心思想是：通过综合状态之间的转移概率和前一个状态的情况计算出概率最大的状态转换路径，从而推断出隐含状态的序列的情况，即在每一步的所有选择都保存了前继所有步骤到当前步骤当前选择的最小总代价（或者最大价值）以及当前代价的情况下后续步骤的选择。依次计算完所有步骤后，通过回溯的方法找到最优选择路径。
简单来说，在计算第t+1时刻的最短路径时，只需要考虑从开始到当前t时刻下k个状态值的最短路径和当前状态值到第t+1状态值的最短路径即可。如求t=3时的最短路径，等于求t=2时的所有状态结点x2t（见上图-2所示）的最短路径再加上t=2到t=3的各节点的最短路径。
一个例子：
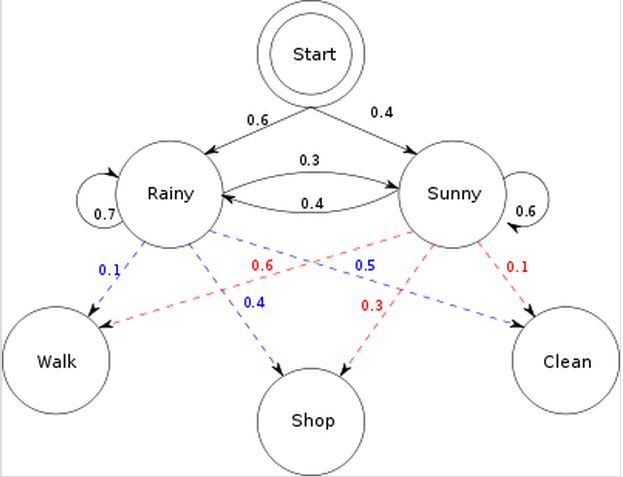
这张图就告诉了我们HMM的模型参数
初始概率π=[ 0.6 0.4]
转移概率（天气(隐状态)之间互相转移）
| rain | sun | |
| rain | 0.7 | 0.3 |
| sun | 0.4 | 0.6 |
| walk | shop | clean | |
| rain | 0.1 | 0.4 | 0.5 |
| sun | 0.6 | 0.3 | 0.1 |
求解：三天对应最可能的天气状态
解答：
【注】δ的下标不是代表第几天，而是当前天的第几个隐状态
①首先初始化，对于每一个天气状态，求当天对应行为的概率
初始化，即第一天不用找最大值，因为第一天哪里知道最可能的路径，路径是链接两个节点的，一个节点无法称为路径
②第一天到达第二天的路径概率
③第二天到第三天的路径概率
④回溯
找到最后一天最大的概率
发现第三天对应第一个状态的概率最大，而且此概率通过③中的ψ1是第二天的第一个状态ψ1到达第三天的第一个状态得到的，所以第二天对应的应该是第一个状态。
而到达第二天的第一个状态的最大概率是第一天的第二个状态，通过②中的ψ1能够看出来。
所以合起来就是第一天的第二个状态->第二天的第一个状态->第三天的第一个状态
即三天天气应该是（sun，rain，rain）
public class Viterbi {
private static class TNode {
public int[] v_path; // 节点路径
public double v_prob; // 概率累计值
public TNode( int[] v_path, double v_prob) {
this.v_path = copyIntArray(v_path);
this.v_prob = v_prob;
}
}
private static int[] copyIntArray(int[] ia) { // 数组拷贝
int[] newIa = new int[ia.length];
System.arraycopy(ia, 0, newIa, 0, ia.length); // 较wiki源码有改动
return newIa;
}
private static int[] copyIntArray(int[] ia, int newInt) { // 数组拷贝
int[] newIa = new int[ia.length + 1];
System.arraycopy(ia, 0, newIa, 0, ia.length); // 较wiki的源码稍有改动
newIa[ia.length] = newInt;
return newIa;
}
// forwardViterbi(observations, states, start_probability,
// transition_probability, emission_probability)
public int[] forwardViterbi(String[] y, String[] X, double[] sp,
double[][] tp, double[][] ep) {
TNode[] T = new TNode[X.length];
for (int state = 0; state < X.length; state++) {
int[] intArray = new int[1];
intArray[0] = state;
T[state] = new TNode(intArray, sp[state] * ep[state][0]);
}
for (int output = 1; output < y.length; output++) {
TNode[] U = new TNode[X.length];
for (int next_state = 0; next_state < X.length; next_state++) {
int[] argmax = new int[0];
double valmax = 0;
for (int state = 0; state < X.length; state++) {
int[] v_path = copyIntArray(T[state].v_path);
double v_prob = T[state].v_prob;
double p = ep[next_state][output] * tp[state][next_state];
v_prob *= p; // 核心元语
if (v_prob > valmax) { // 每一轮会增加节点
if (v_path.length == y.length) { // 最终截止
argmax = copyIntArray(v_path);
} else {
argmax = copyIntArray(v_path, next_state); // 增加新的节点
}
valmax = v_prob;
}
} // the number 3 for
U[next_state] = new TNode(argmax, valmax);
} // the number 2 for
T = U;
}
// apply sum/max to the final states:
int[] argmax = new int[0];
double valmax = 0;
for (int state = 0; state < X.length; state++) {
int[] v_path = copyIntArray(T[state].v_path);
double v_prob = T[state].v_prob;
if (v_prob > valmax) {
argmax = copyIntArray(v_path);
valmax = v_prob;
}
}
return argmax;
}
}