贝叶斯定理推导

主要是还想再过一遍贝叶斯公式的推导

1.条件概率

设A,B是两个事件，且P(B)>0,则在事件B发生的条件下，事件A发生的条件概率（conditional probability)为：

P(A|B)=P(AB)/P(B)

2.乘法公式和乘法定理

已经了解了条件概率之后，方程两边同时乘P（B）得到的就是乘法公式

*P(AB)=P(A|B)P(B)=P(B|A)P(A)

这个公式还可以进一步推广，当不仅有A，B两个事件，而是有A1，A2…An个事件时：

P(A1A2…An)=P(An|An-1An-2…A1)P(An-1An-2…A1)=P(An|An-1An-2…A1)P(An-1|An-2An-3…A1)P(An-2An-3…A1)=P(A1)P(A2|A1)P(A3|A1A2)…P(An|A1A2…An-1)

即：P(A1A2…An-1An)=P(A1)P(A2|A1)P(A3|A1A2)…P(An|A1A2…An-1)

3.全概率公式

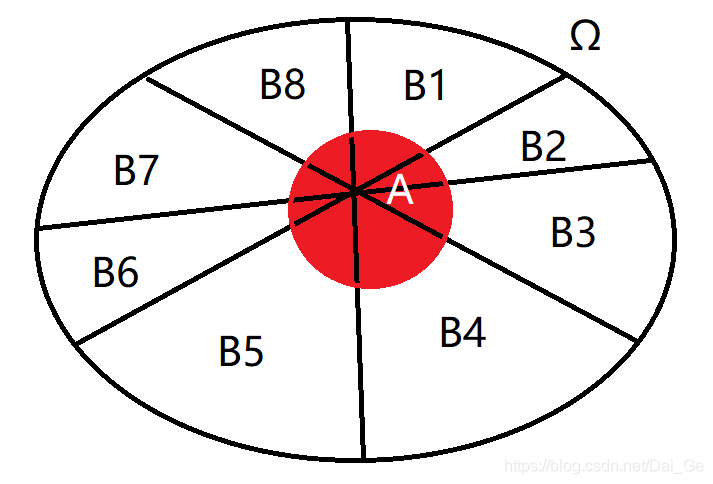
如果事件组B1，B2，… 满足

​ 1.B1，B2…两两互斥，即 Bi ∩ Bj = ∅ ，i≠j ， i,j=1，2，…，且P(Bi)>0, i=1,2,…;

​ 2.B1∪B2∪…=Ω ，则称事件组 B1,B2,…是样本空间Ω的一个划分

​ 设 B1,B2,…是样本空间Ω的一个划分，A为任一事件，则：

P(A)=P(AB1)+P(AB2)+…+P(ABn)

此时代入乘法公式有：

P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+…P(A|Bn)P(Bn)

上面这个公式就是全概率公式

全概率公式是由多种原因或多种方式推结果的概率。表示达到某个目的，有多种方式（或者造成某种结果，有多种原因），问达到目的的概率是多少（造成这种结果的概率是多少）？

就比如说小明从A小和A大到达A点的概率分别是0.3和0.7，从A小顺利到达A点的概率是0.4，从A大顺利到达的概率是0.9，那么问警方顺利到达A点的概率是多少？

解：假设X代表事件小明顺利到了A点

P(X)=P(X|A小)P(A小)+P(X|A大)P(A大)=0.4×0.3+0.7×0.9=0.75

4.贝叶斯公式

贝叶斯公式和全概率公式相反，贝叶斯公式是针对某个结果，求导致这种结果的某种原因或某种方式的概率（所谓执果求因）

针对全概率公式中应用的场景在贝叶斯公式中可以改成：

小明顺利到达了A点，问是经过A小到达的概率是多少？

首先这个问题的答案不应该是0.4，在全概率公式应用的场景时，0.4是小明不明白自己能否顺利到达A点的概率，0.4这个概率是我们研究者之前经过大数据统计发现人们在对前方一无所知的前提下，从某个位置到A点选择A小的概率。而现在我们已经清楚了小明已经顺利到达了，在此基础上，问是从A小经过的概率是多少，因此不能简单的直接得出。

那么该怎么计算呢？

还是跟之前一样，我们记X为小明顺利达到A点的事件，那么根据条件概率公式可以得到：

小明在成功达到A点的前提下从A小经过的概率是：P(A小|X)=P(A小，X)/P(X)

根据乘法公式有：P(A小，X)=P(X|A小)P(A小)

结合上述两个式子有：P(A小|X)=P(X|A小)P(A小)/P（X）

P(X)的值我们之前算过了是：P(X)=P(X|A小)P(A小)+P(X|A大)P(A大)=0.4×0.3+0.7×0.9=0.75

因此P(A小|X)=P(X|A小)P(A小)/P(X|A小)P(A小)+P(X|A大)P(A大)=0.4×0.3×0.75=0.09

上面那个P(A小|X)=P(X|A小)P(A小)/P（X）=P(X|A小)P(A小)/P(X|A小)P(A小)+P(X|A大)P(A大)就是传说中的贝叶斯公式

公式描述：

公式中，事件Bi的概率为P(Bi)，事件Bi已发生条件下事件A的概率为P(A│Bi)，事件A发生条件下事件Bi的概率为P(Bi│A)。

（关于贝叶斯公式更详细的内容这里暂且不深入讨论，以后可能会找机会补充上）