选择排序
选择排序是一种很简单直观的排序算法,主要思想就是每次从待排序的元素中选择出最大或最小的那个元素,然后将其放至已排序序列的末尾,直到全部待排序序列都排序完毕。
排序要点
1.初始状态时,待排序序列为a1,a2,…an,已排序序列为空。
2.第一趟排序,从待排序序列中找到最大或最小元素ak,将其与待排序序列的第一个元素a1对换,此时已排序序列为ak,长度为增加1,待排序序列长度减少1,变为n-1,其中ak被抽走了。
3.第二趟排序,从待排序序列中找到最大或最小元素aj,将其与待排序序列的第一个元素a2对换,此时已排序序列为ak,aj,长度增加1,变为2,待排序序列长度减少1,变为n-2,其中aj又被抽走了。
4.不断进行上面的排序操作,直到经过n-1趟排序后完成整个序列的排序。最终待排序序列为空,已排序序列长度为n。
排序过程
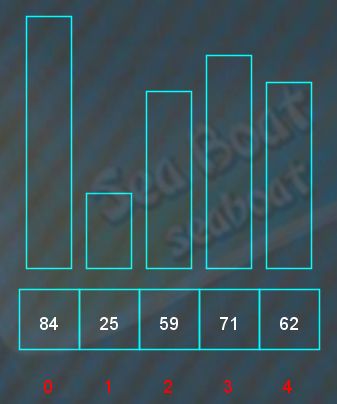
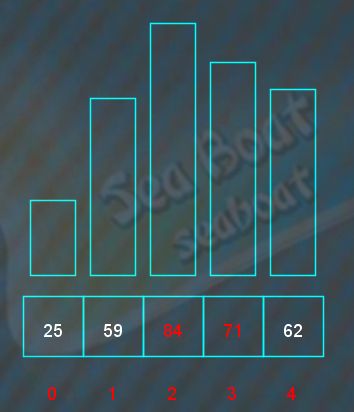
假设我们有如下5个元素,分别为84,25,59,71,62,现在进行选择排序。
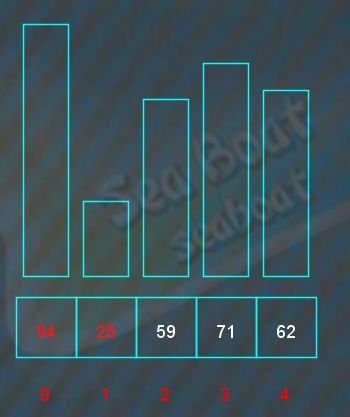
第一趟,此时待排序序列为84,25,59,71,62,任务是从中找到最小元素,并与第一个元素调换作为已排序序列的第一个元素。最小元素可以通过逐一比较找到。头两个元素比较,较小的是25,
接着下一个元素59与25比较,较小的是25,
接着下一个元素71与25比较,较小的是25,
接着下一个元素62与25比较,较小的是25,完成全部元素比较,最小元素为25。
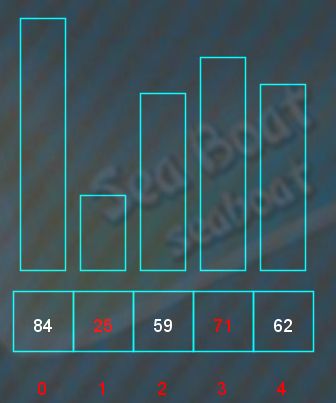
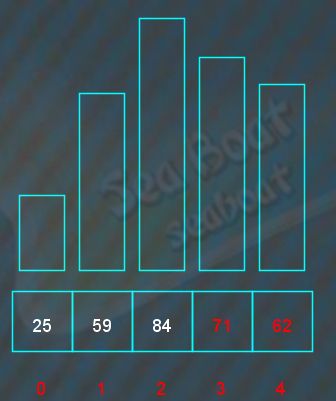
最小元素对调到原来待排序序列的第一个位置,即是放到已排序序列的尾部,此时已排序序列只有一个元素。而下一趟的待排序序列为84,59,71,62,继续寻找最小元素,84与59比较,59较小,
接着下一个元素71与59比较,较小的是59,
接着下一个元素62与59比较,较小的是59,完成全部元素比较,最小元素为59。
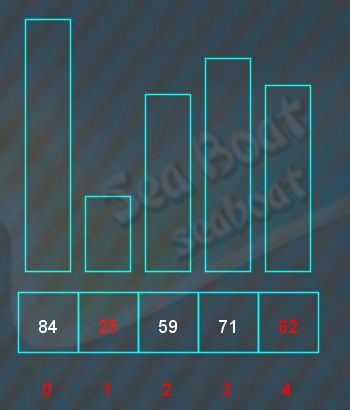
最小元素对调到原来待排序序列的第一个位置,即是放到已排序序列的尾部,此时已排序序列有两个元素。而下一趟的待排序序列为84,71,62,继续寻找最小元素,84与71比较,71较小,
接着下一个元素62与71比较,较小的是62,完成全部元素比较,最小元素为62。
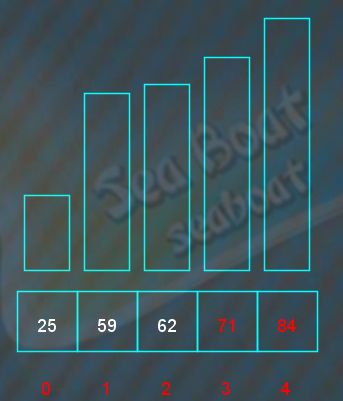
最小元素对调到原来待排序序列的第一个位置,即是放到已排序序列的尾部,此时已排序序列有三个元素。而下一趟的待排序序列为71,84,继续寻找最小元素,71与84比较,71较小,
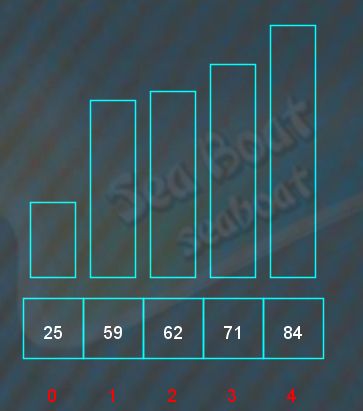
71为最小元素,对调到原来待排序序列的第一个位置,即是放到已排序序列的尾部,此时已排序序列有四个元素。下一趟只待排序序列只剩一个元素了,无需继续比较,直接添加到已排序序列的尾部,完成整个排序工作。
稳定性
排序的稳定性主要是指在待排序序列中,存在多个具有相同值的元素,如果经过某种排序算法后这些相同值的元素之间相对次序保持不变,则称该排序算法是稳定的。而如果它们之间相对次序打乱了,则为不稳定。
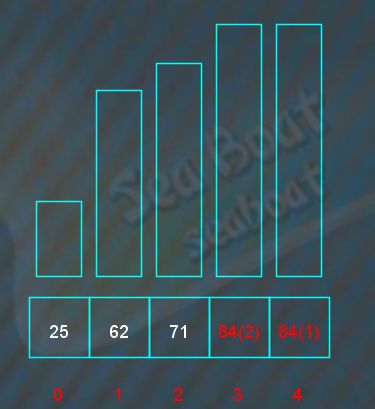
选择排序为不稳定排序算法。
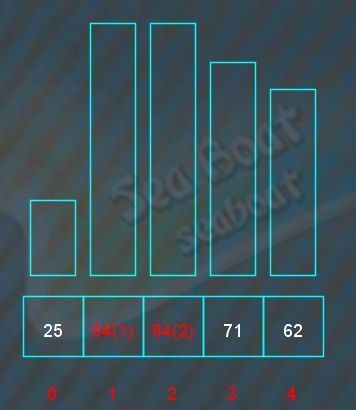
假设我们要排序的序列为84,25,84,71,62,这其中包含了两个值为84的元素,按照选择排序方法对其进行排序。
第一趟排序,元素25和第一个元素84对调,
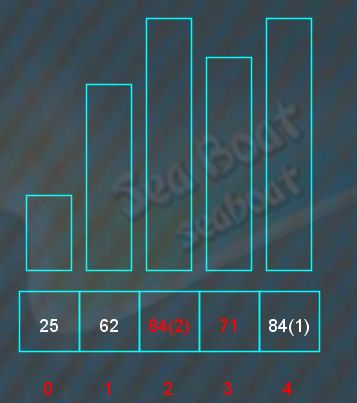
第二趟排序,元素62和第一个元素84对调,
第三趟排序,元素71和第二个元素84对调,
最终的状态如下,可以看到两个值为84的元素的次序已经变化了。
转自:https://blog.csdn.net/wangyangzhizhou/article/details/81734912