normalization总结和实现
本博文大量引用张俊林老师的专栏:https://zhuanlan.zhihu.com/p/43200897
内化于己
默认你已经略懂BN,至少读过batch normalization论文!
介绍
normalization分为针对输入激活函数数据和权重两种方式。
1.输入激活函数数据
最为广泛使用的就是BatchNormalization(BN),它是一种典形的对输入数据的norm操作,包括它的变种LayerNormalization(LN) / InstanceNormalization(IN) / GroupNormalization(GN) 都是针对输入进激活函数的数据进行norm
... → CONV/FC → BN → active function → dropout → ....
大概是这么个顺序排列(BN论文是这样)
进行的操作也是极为相似,只不过针对不同集合S求mean和std。
2.权重
可能会用到的WeightNormalization(WN)
这部分暂时不是很懂,以后再写 (滑稽)
BN
BatchNormalization方法,相信看过论文的都知道是针对一个batch不同example的同一个输入位置进行norm,再用两个可训练的参数表示该数据的mean和std。
论文解决了 Internal Covariate Shift 问题
(虽然之后又有人diss并不是,但我们还是按照步骤走下去吧)
算法的步骤就是:
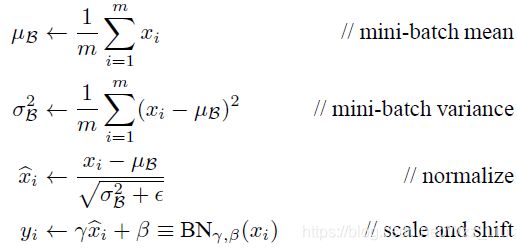
如图,前三步将数据变成 (0,1)的高斯分布,最后一步又给它一个可学习的mean和std,其实我也对着步的原理抱有怀疑!姑且认为,一堆数据的这个分布的mean和std不好更改,引入两个可训练得变量,就很容易改变数据得分布,加快了训练;同时尊重输入BN前的数据分布 - -!
但BN效果就是很显著,所以,你牛逼你说啥都对~
下面具体讲在FC和CNN的BN不同之处
for fully-connect
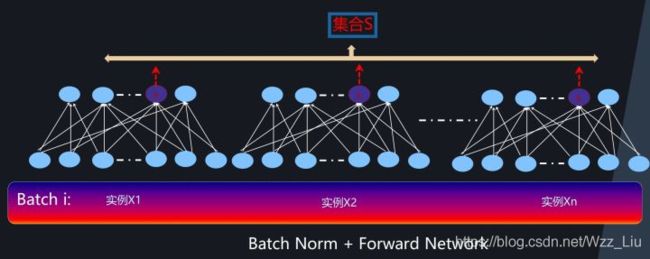
如图,不同example的同一位置进行norm,然后再学的自己的β和γ,其中每个神经元都有这么一对参数。
CNN
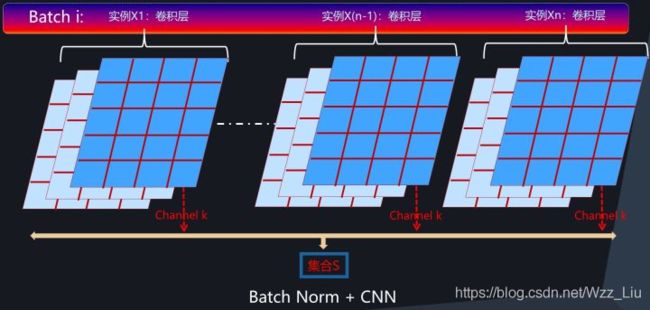
如图batch内的不同example的同一个channel集合为S,对一个 N ∗ H ∗ W ∗ C i n N*H*W*C_{in} N∗H∗W∗Cin到 N ∗ H ∗ W ∗ C o u t N*H*W*C_{out} N∗H∗W∗Cout的卷积中,需要 C i n ∗ K H ∗ K W C_{in}*K_H*K_W Cin∗KH∗KW的卷积核 C o u t C_{out} Cout个,但是只需要 C i n C_{in} Cin对β和γ,我之前一直以为要 C i n ∗ C o u t C_{in}*C_{out} Cin∗Cout对 - -!因为是对数据的norm,和卷积核是什么没关系。
先简单用代码表示下:
# train时
batch_mean = np.mean(data, axis=[0,1,2])
batch_std = np.std(data, axis=[0,1,2])
# inference 因为没有batch的概念,则需要保存一个滑动平均mean和滑动平均std
ema = tf.train.ExponentialMovingAverage(moving_decay)
ema_apply_op = ema.apply([batch_mean,batch_std])
out = (data - mean)/std * gamma + beta # C_in对gamma/beta
#inference时
out_inf = (data_inf - ema.average(batch_mean))/ema.average(batch_std) * gamma + beta # C_in对gamma/beta
为什么除了BN还要有各种不一样的N,当然是因为BN有他的缺点:
-
太过依赖batch_size的大小了
当batch较小时,以我们直观的感觉是不合理的,因为分布和实际很可能很不一样,事实也是如此。 -
对于一些动态的网络结构不太适用 如:RNN
对于RNN的输入维度[N,T,C],做BN的话,应该对前两个维度做norm,但是T又是变长的,并且串行,所以很不方便。
更详细的解释在文章最后! -
在inference使,没有batch的概念
所以要保存一对滑动平均的β和γ
LN
算法步骤和BN完全一样,只是在S集合的选择不一样了。
他进行norm和batch_size(即N)没有关系。
for fully-connect
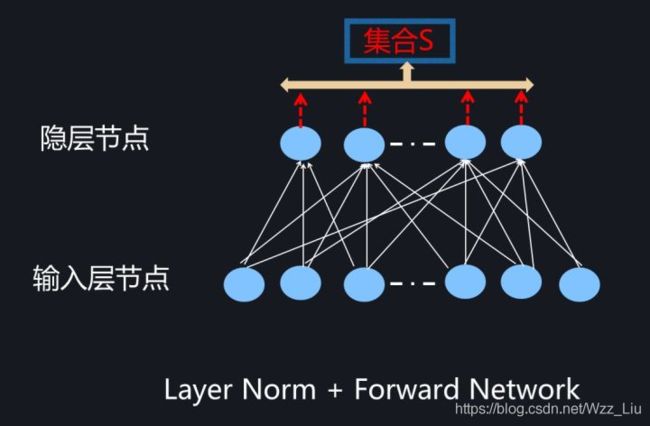
对batch中每个example计算隐层的所有节点做norm
for CNN
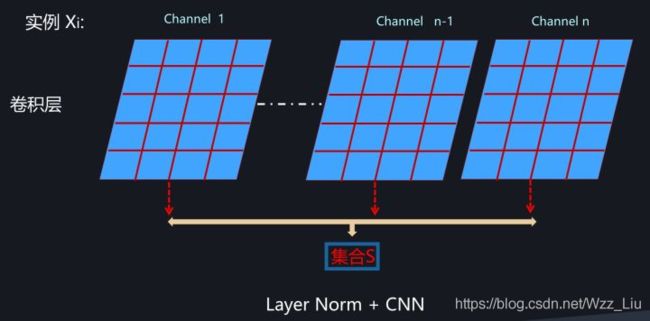
如图,。对一个 N ∗ H ∗ W ∗ C i n N*H*W*C_{in} N∗H∗W∗Cin到 N ∗ H ∗ W ∗ C o u t N*H*W*C_{out} N∗H∗W∗Cout的卷积中,对于batch中一个example的不同channel进行norm计算。
先简单用代码表示下:
mean = np.mean(data, axis=[1,2,3])
std = np.std(data, axis=[1,2,3])
out = (data - mean)/std * gamma + beta # C_in对gamma/beta
results = gamma * out+ beta
# 对此,我也是非常的难以理解,为什么TF中实现是 C_in对gamma/beta;
# torch中实现是 H*W*C_in对gamma/beta; 按BN的做法,正常不应该是N吗?????
# 只能解释道:对H W C三个维度进行norm操作,已经使得数据变得更加易于训练;
# 再加多少对gamma/beta都是为了,数据的分布更加容易被改变,
# 毕竟不这么变的话,你就得改变上一层所有的权重来达到相同目的
# 并且,为了不于N有任何关系,不使用N。
for RNN
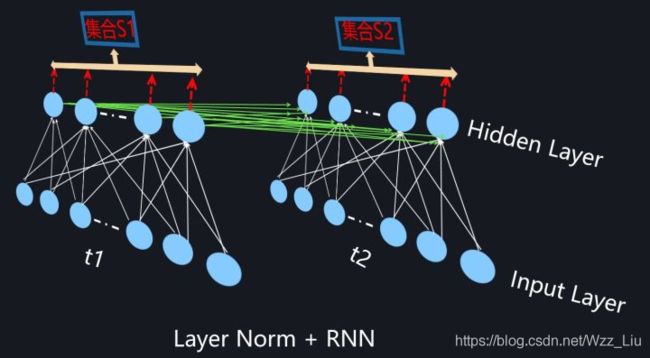
其实RNN上做LN,又是一个复杂的过程了,我直接给各位亲分析tf源码吧
tf中只有这么个类(另一个是一样的)实现了LN:
(删去了大堆的无关代码,且以下都是tf有关)
class LayerNormBasicLSTMCell(rnn_cell_impl.RNNCell):
def __init__(self,
num_units,
forget_bias=1.0,
input_size=None,
activation=math_ops.tanh,
layer_norm=True,
norm_gain=1.0,
norm_shift=0.0,
dropout_keep_prob=1.0,
dropout_prob_seed=None,
reuse=None):
super(LayerNormBasicLSTMCell, self).__init__(_reuse=reuse)
...
def _norm(self, inp, scope, dtype=dtypes.float32):
shape = inp.get_shape()[-1:]
gamma_init = init_ops.constant_initializer(self._norm_gain)
beta_init = init_ops.constant_initializer(self._norm_shift)
with vs.variable_scope(scope):
# Initialize beta and gamma for use by layer_norm.
vs.get_variable("gamma", shape=shape, initializer=gamma_init, dtype=dtype)
vs.get_variable("beta", shape=shape, initializer=beta_init, dtype=dtype)
normalized = layers.layer_norm(inp, reuse=True, scope=scope)
return normalized
...
def call(self, inputs, state):
"""LSTM cell with layer normalization and recurrent dropout."""
c, h = state
args = array_ops.concat([inputs, h], 1)
concat = self._linear(args)
dtype = args.dtype
i, j, f, o = array_ops.split(value=concat, num_or_size_splits=4, axis=1)
if self._layer_norm:
i = self._norm(i, "input", dtype=dtype)
j = self._norm(j, "transform", dtype=dtype)
f = self._norm(f, "forget", dtype=dtype)
o = self._norm(o, "output", dtype=dtype)
g = self._activation(j)
if (not isinstance(self._keep_prob, float)) or self._keep_prob < 1:
g = nn_ops.dropout(g, self._keep_prob, seed=self._seed)
new_c = (
c * math_ops.sigmoid(f + self._forget_bias) + math_ops.sigmoid(i) * g)
if self._layer_norm:
new_c = self._norm(new_c, "state", dtype=dtype)
new_h = self._activation(new_c) * math_ops.sigmoid(o)
new_state = rnn_cell_impl.LSTMStateTuple(new_c, new_h)
return new_h, new_state
上面的LNLSTMCell,调用了layers.layer_norm(),这说明,ln是在每个时间步做的,并且self._norm()方法有5次被调用,仔细查看被调用的位置,可以看见,在lstm中4个gate进入激活函数sigmoid前,和新的cell进入激活前;这很符合我们对BN/LN的认识
... → CONV/FC → BN → active function → ....
//
另外,提一下,lstm的dropout只在表示lstm’学习’时使用,即放在tanh激活之后,input门相乘之前
本人的另一篇博文精简地讲述了lstm地相关知识:https://blog.csdn.net/Wzz_Liu/article/details/85038746
如果不知道三个门的童鞋,建议右上角关闭,等你懂了再来看~
继续,因为RNN展开实际上都是本质都是fully-connect,搭上了不一样的结构和激活,就有了它的实际意义layers.layer_norm()函数其实就是针对fully-connect和CNN做layer_norm的函数。传入layers.layer_norm()的inp实际就是某个时间步长的输入形如[N,C],layer_norm对C这个维度做norm,再接C对可训练的γ和β参数。所以对于LNLSTMCell来说,共有5*C对γ和β参数,所有时间步长共享参数。
LN总结
讲了这么多,反正LN用在CNN上远不如BN效果好;而LN用在RNN上,效果非常好。
LN完全不需要N的任何信息。
IN
InstanceNormalization(IN)本质上只适合在CNN上用,因为他是对batch的每个example的每个channel都做norm
fully-connect:我他妈每个channel就一个scalar
rnn:我也是
for CNN
 如图batch内的不同example的不同一个channel集合为S,对一个 N ∗ H ∗ W ∗ C i n N*H*W*C_{in} N∗H∗W∗Cin到 N ∗ H ∗ W ∗ C o u t N*H*W*C_{out} N∗H∗W∗Cout的卷积中,对H * W 维度求norm后,需要 C i n C_{in} Cin对β和γ
如图batch内的不同example的不同一个channel集合为S,对一个 N ∗ H ∗ W ∗ C i n N*H*W*C_{in} N∗H∗W∗Cin到 N ∗ H ∗ W ∗ C o u t N*H*W*C_{out} N∗H∗W∗Cout的卷积中,对H * W 维度求norm后,需要 C i n C_{in} Cin对β和γ
先简单用代码表示下:
mean = np.mean(data, axis=[1,2])
std = np.std(data, axis=[1,2])
out = (data - mean)/std * gamma + beta # C_in对gamma/beta 为什么是C_in理由同上
results = gamma * out+ beta
GN
group normalization
我们想啊,IN和LN分别是对每个channel和对所有channel做norm,那我能不能折中以下呢?
那结果就是GN,讲所有channel分成G组,对于:
fully-connct:[N,C] → [N, G, C/G]
CNN: [N, H, W, C] → [N, H, W, C/G, G]
for CNN
N, H, W, C = data.shape
data = tf.reshape(data, (N, H, W, C/G, G))
mean = np.mean(data, axis=[1,2,3])
std = np.std(data, axis=[1,2,3])
out = (data - mean)/std * gamma + beta # G对gamma/beta 为什么是G理由同上
results = gamma * out+ beta
fully-connect下也是一样的,只不过没有了H W两个维度的东西。
而对于RNN,理解了沿着time展开,你就会发现,和fully-connect没有区别,只不过权重共享而已。
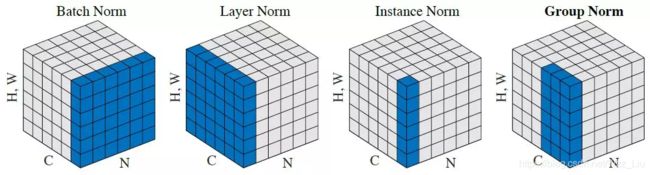
最后图形化地理解下什么叫RNN的LN和BN
下图就很形象地描绘了不同normalization作用的维度,RNN中无非就是把H,W这两个维度换成T维度,但是是变长的,且只能一格一格走。
对于RNN的图,引用我在知乎的问题,感谢答主解惑!
https://www.zhihu.com/question/308310065
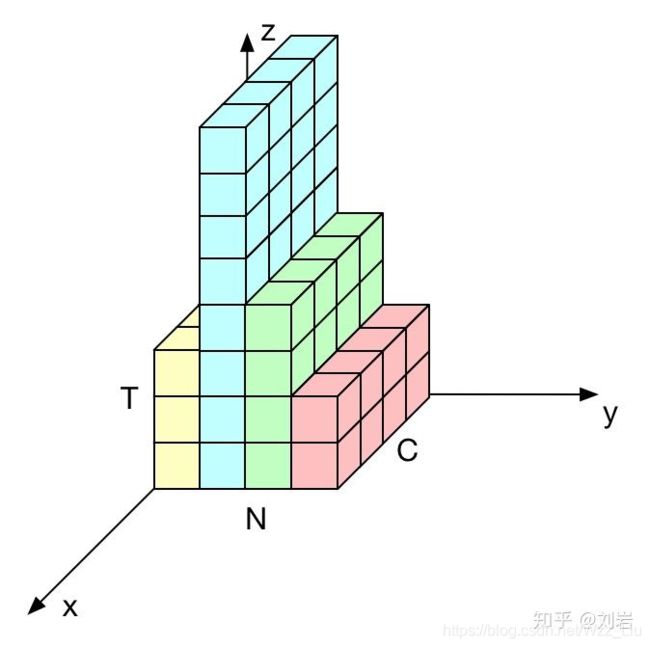
为什么BN不行,这里最后再次详细解释:
对于BN按[N,T]做norm。由于BN中每个样本的长度都不一样,计算的 μ 和 σ 时就会非常不具有代表性,当t>3时,我们只能获得来自第二个样本的一个统计量,那么此时的均值和方差已经没有意义。
LN是按[C,T]做norm,这个被证明是在RNN中表现比较好的一种归一化方法,因为在每个时间片都会获得相同的数量(通道数)个数值的归一化统计量。LN中不同时间片的β和γ是共享的。
开脑洞地在[N,C]维度做norm的话,每个时间片一个独立的β和γ,就不知道要确定多少个 β和γ了,因为T不定。况且,T越往后走,越有可能都是pad。
.#
