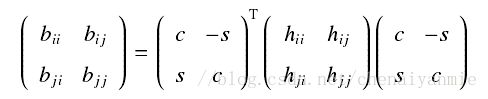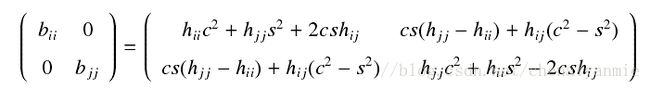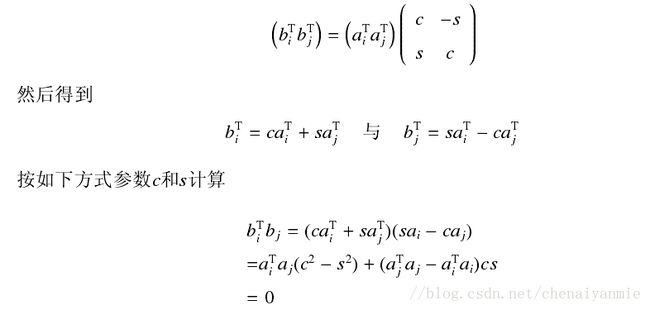基于QR分解与Jacobi方法的SVD分解

基于QR分解方法的SVD分解：

矩阵的 SVD 分解并不唯一。主要的并行算法子程序都是基于经典求解矩阵奇异值的串行方法而实现的。

基于 QR 迭代求解矩阵奇异值的方法，是求解双对角矩阵所有奇异值最快速的算法，求解出的奇异值可以达到较高的相对精度；

分而治之方法，它是求解全部矩阵奇异值和奇异向量速度很快的算法，但是当求解微小的奇异值时，往往不能保证很高的相对精度，对于一般应用来说，分而治之算法求解出的奇异值已经足够精确；

对分法和逆迭代方法，它求解矩阵奇异值可以保证奇异值达到较高的相对精度，但是求解出的奇异向量偶尔会损失正交性；

Jacobi 方法，该方法求解出的矩阵奇异值拥有较高的相对精度、求解出的奇异向量正交性好、有较强的数值稳定性，并且算法实现简单有利于并行，成为求解矩阵奇异值问题中一个活跃的研究课题。

参考：徐士良C常用算法程序集(第二版)
机器学习之旅—奇异值分解

设矩阵 A∈Rm×n ，对于矩阵 A 的SVD分解的时间复杂度在 m 大于n 的情况下，为 O(m×n2) ；

基于Jacobi方法的SVD分解

经典（双边）Jacobi方法：

由SVD分解的形式： A=UΣVT 可得， ATA=VΣ2VT ， VT(ATA)V=Σ2 为对角阵，所以正交矩阵 V 为A的右奇异向量，也为 ATA 的特征向量，

同理可得：矩阵 U 为矩阵 A 的左奇异向量，也为 AAT 的特征向量。

因此双边Jacobi方法的核心思想是：将对称矩阵 ATA 转化为对角矩阵，其转化矩阵即为右奇异矩阵 V

步骤：选择Jacobi矩阵 J ，类似Givens矩阵 G （标准正交矩阵）， J=GT

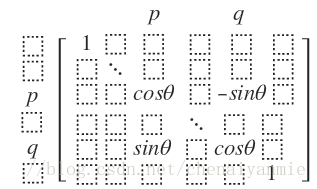
Jacobi 矩阵可以将 i 行 j 行与 i 列 j 列的四个角点上的元素进行正交变换， 使非对角线上的元素 Ai,j 化为0，将矩阵 A 经过右连乘 Ji,j 矩阵将上对角线元素全部化为0，并 左连乘 Gi,j 矩阵将下对角线元素全部化为0（数值计算中可能为一个很小的数字也可）,矩阵 A 为对称矩阵， Ai,j=Aj,i ：

JTk...JT2JT1(ATA)J1J2...Jk=Λ=Σ2 ；

因此右奇异矩阵 V=J1J2...Jk ，标准正交阵的连乘也为标准正交阵；

奇异值 σ 为对角阵 Λ 的对角元素的开方，选择非零奇异值对应的特征向量 Vi 按奇异值大小排列；

根据公式 Ui=AViσ ，求取左奇异向量U ；

具体推导：因为 J(i,j,θ) 仅仅影响与 i 和 j 相应行和列的元素，其它矩阵元素不会受到影响，所以可以使用二阶主子式来描述旋转变换的过程。

当变换结束后，矩阵中(i,j)与(j,i)的元素同时变为零。并且每一次变换结束后，非对角线元素的弗洛贝尼乌斯范数（F - 范数，为元素的平方和开发） 的平方和减少 2h2i,j ，所以每经过一次旋转变换，F - 范数越趋于0，经过反复的旋转变换，算法达到收敛条件而停止。为了得到特征向量，可以在算法开始之前设置单位矩阵 I 来保存所有的旋转变换 Ji ，当分解结束后原来的单位矩阵就变为保存特征向量的矩阵 V=IJ1J2J3 · · · 。为了尽快消去所有非对角线元素，经典 Jacobi 方法在每一次对矩阵进行旋转变换时，都选取非对角线元素中绝对值最大的元素，如果该元素小于预期的精度，算法收敛，得到矩阵的奇异值分解，否则继续进行变换直到达到精度要求。整个算法是二次收敛的。

由于经典 Jacobi 算法每一次进行旋转变换前都需要在 n(n−1)/2 个非对角线的元素中选取绝对值最大的元素，这需要花费 O(n2) 的时间对矩阵进行遍历，而执行旋转变换的代价仅为 O(n) ，故对于维数大的矩阵，搜索时间将占支配地位，导致算法效率过低。

改进方法如下：

1.按照行或者列的顺序循环旋转变换非对角线元素，经过若干轮变换后非对角线的元素值均小于精度要求，渐进二次收敛。

2.设定门限阈值 w ，大于阈值的非对角元素进行旋转变换，一轮后，缩小阈值 w ，再旋转变换，直到均小于精度要求。

3.每次变换开始之前，先将矩阵中每一列非对角线元素按绝对值从大到小排序，当消去非对角线元素时，消去与前一个消去元素不在同一行的绝对值最大的元素。由于每一次旋转变换前后之间选取的元素既不在同一行也不在同一列，不会发生变换上的数据冲突，因此该算法可以很好的被并行化；再改进，可以加上门限阈值 w 来加速收敛。

单边Jacobi方法：

由 SVD 分解形式： A=UΣVT ，可得 UΣ=AV ； UΣ 为正交矩阵，因此 AV 也为正交矩阵，如何通过一系列的线性变换将矩阵 A 转换为正交矩阵就是单边Jacobi方法的核心，Jacobi 变换正好满足这个需求。

因此单边Jacobi方法的核心思想是：采用一系列 Jacobi 平面旋转变换，对维度矩阵 Am×n 进行正交化；

B=A(J1J2J3...) ，使得 B 中任意两列向量满足 bjTbj=0 ，然后对 Bm×n 归一化得到

B=UΣ , Σ=diag(σ1,σ2,...σn−1,σn) , σi=bTibi

V=J1J2J3 · · · 是由一系列 Jacobi 旋转变换矩阵相乘而得，因此它本身也是正交矩阵。整理后就可以得到矩阵A的奇异值分解。

设正交化最后得到的矩阵为 B=A(J1J2J3...) 为正交矩阵， bTi ， bTj ， aTi ， aTj 分别为矩阵的一列，由于在采用 Jacobi 方法求解矩阵奇异值时仅从一个方向对矩阵进行旋转变换，因此称之为单边 Jacobi 。对矩阵进行正交化时，仅仅 i 与 j 两列元素受到影响，具体的变换过程如下：

在 J=(i,j,θ) 对矩阵旋转变换之前，如果 ∥ai∥>∥aj∥ ，那么 ∥bi∥>∥bj∥ ( ∥x∥ 为向量 x 的2阶范数)。

因为B中任意两列向量都要彼此正交之后，算法才可以收敛，因此一共需要对 A 进行 N(N−1)/2 次旋转才能使得矩阵中所有列之间都正交一次。由于Jacobi旋转变换中对c和s的计算是决定单边Jacobi方法收敛速度的主要原因之一，因此后续学者对此提出了多种改进方法。

Hestens设计了一种新的单边 Jacobi方法。在该方法种，当矩阵 A 中向量 ||ai||<||aj|| 时，先交换两列元素，然后再利用平面旋转变换，按照循环序列对矩阵进行正交变换。这个方法可以保证最终求解的奇异值是按照非增序列排列好的。

单边 Jacobi 方法中平面旋转变换仅影响相应的两列元素，因此通过合理划分，可以并行的实现相互之间不存在依赖关系的列对进行变换。因此为了保证在合理的迭代次数下并行的完成 n(n−1)/2 次旋转变换，需要设计一个“好的”数据交换序列。

1.Caterpillar-Track序列：(n=6)

(n=5) :

2.奇 - 偶序列：可以先将矩阵每列按照非增序列排列好，再进行正交旋转变换

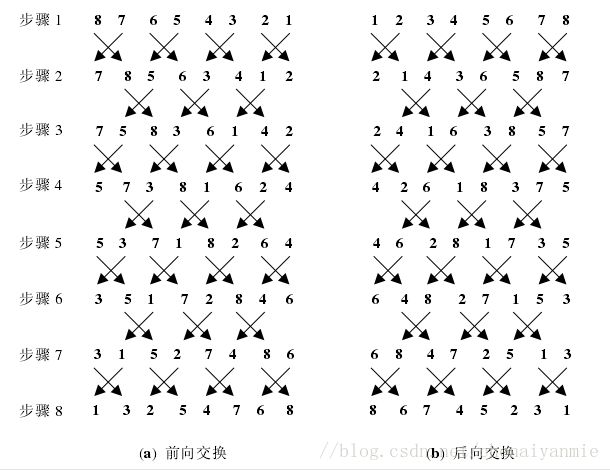
前向交换：每一阶段结束后，将原来形成的索引列对拆分，8，7，…3，2，1，降序，并按照从左向右依次递增的顺序进行交换（交换仅仅发生在索引对内部），最后的序列排序为1，2，3…，7，8，升序，奇异值序列为非增排列。

并行单边Jacobi方法

采用单边 Jacobi 方法在 p 个计算节点上并行求解矩阵奇异值时，一般将矩阵按列划分成块：

A=[A1,A2,...Ar] ， Ai 中包含 ni 列元素向量 （n1+n2+...+nr−1+nr=n） ，为了得到保存右奇异向量的矩阵 V ，可以先设置一个单位矩阵 I ，将其同样划分成块： I=[I1,I2,...Ir] ，

划分结束后，对所有列块从小到大依次标注上索引号将 Ai 与 Ii 一同发送到各个计算节点，每一个节点获取两个列块。所有计算节点对本身含有两个的列块 Ai 与 Aj 进行旋转变换并更新 Ii 与 Ij ，即将每个 Ai 作为矩阵 A 进行单边 Jacobi 旋转变换得到 Bi ，实现 Ai 的SVD分解。然后按照前面描述的数据交换序列在 p 个计算节点中传递 Ai 、 Aj 与 Ii 、 Ij 。 在每个计算节点内对列块进行变换的方式主要分为以下两种：

1. 在每一轮计算之初，各个节点首先对自身包含的两个列块 Ai 与 Aj 采用单边循环 Jacobi 方法分别进行旋转变换并分别更新 Ii 、 Ij ，再把两个列块作为整体使用同样的方法进行旋转变换，并将 Ii 、 Ij 作为整体一起更新。这时旋转变换与更新操作仅仅发生在列块之间。
   然后所有节点按照变换序列传递列块，为下一阶段变换做准备。由于在每一轮的开始阶段已经对所有列块分别进行旋转变换，因此在剩余阶段的分解过程中，旋转变换仅仅发生在列块之间，而不再对列块内部重复变换。当在某一轮计算时，所有计算节点内的列块都满足收各自的敛条件时，整个分解过程结束。
2. 可以将双边 Jacobi 方法引入到各节点的子问题求解中来。通过对 Jacobi 基础知识的介绍，可以知道单边 Jacobi 方法与双边 Jacobi 方法有着密切的联系。假设矩阵 H=ATA (A 的奇异值分解为 A=UΣVT )，那么 H=ATA=(VΣUT)(UΣVT)=VΣ2VT
   意味着采用单边 Jacobi 方法对矩阵 A 求解奇异值的过程变为对 H 求解特征值的过程，Jacobi 平面旋转变换由对 A 中任意两列向量进行正交变换，变为消去矩阵 H中非对角线元素的过程，即双边 Jacobi 方法。因此求解出的矩阵 [Ai,Aj] 的奇异值的平方即为矩阵 Hi,j=[Ai,Aj]T[Ai,Aj] 的特征值。
   采用双边 Jacobi 方法对其进行奇异值分解： Σ2=VTi,j(Hi,j)Vi,j ，最后对自身包含的列块进行更新： [Ai,Aj]Vi,j与[Ii,Ij]Vi,j

分析：因为在并行求解矩阵奇异值分解时，矩阵的维数 m 往往很大，如果采用第一种方式对矩阵进行旋转变换时，求解c 与s以及相应的更新操作需要耗费大量时间，而且每一个节点在对自身列块进行旋转变换时采用的单边循环 Jacobi 方法大多局限于向量操作(BLAS1)，内存利用率比较低;而在第二种方法中， Hi,j 的维度与 m 相比起来要小很多，因此对 Hi,j 采用双边 Jacobi 方法求解特征值时计算 c 与 s 要节省很多时间，而且在更新列块时可以采用矩阵与矩阵运算(BLAS3)，内存利用率高。

并行计算

并行计算或称平行计算是相对于串行计算来说的。它是一种一次可执行多个指令的算法，目的是提高计算速度，及通过扩大问题求解规模，解决大型而复杂的计算问题。所谓并行计算可分为时间上的并行和空间上的并行。 时间上的并行就是指流水线技术（指在程序执行时多条指令重叠进行操作的一种准并行处理实现技术），而空间上的并行则是指用多个处理器并发的执行计算。

数值并行算法总体上遵循 PCAM 方法学 ，在每个步骤中又会应用具体的设计方法。 PCAM 设计过程分为四 个步骤：划分( Partitioning )、通信( Communication )、组合( Agglomeration )和映射( Mapping ) 。它反映了并行算法设计的基本过程，首先尽量开拓算法的并发性和满足算法的可扩放性，然后着重优化算法的通信成本和全局执行时间，同时通过对整个过程的反复回溯，最终达到一个满意的设计。

并行算法的评估：

1.加速比：加速比是衡量并行算法好坏的标准之一，定义为： S(p)=ts/tp 其中 ts 表示在单处理器上运行最好的顺序算法所需执行时间，而 tp 表示在并行计算相同问题时所需执行时间。

2.效率：并行程序的效率是度量处理器用于有用计算时间的比例，它是处理器利用率的度量标准之一。效率 E 被定义为： E=ts/(tp×p) 它可写成： E=S(p)/p×100% 其中 E 以百分比形式表示。p 为处理器数量。

3.计算/通信比：在所有的并行算法中都涉及到将数据和任务进行分解，分配到不同的处理器上执行这一过程，执行当中也会有数据传递或是数据同步，这都是很大的开销。因此，并行算法的执行时间变为： tp=tcomm+tcomp ；其中 tcomm 是通信时间，而 tcomp 是计算时间。 由于将计算任务分成可以并行执行的子任务，而且与整个任务相比这些子任务都非常小，计算时间与整个任务的执行时间相比也会减小，但是子任务之间的通信时间通常会增加。到达某一点后，通信时间将会成为整个执行时间的主要部分，从而增加并行执行的时间。这时减少通信开销就变得非常关键。因此计算/通信比 F 成为判断并行算法优劣的标准之一，定义如下： F=tcomp/tcomm 。

4.可扩展性( scalability)：可扩展性指的是在确定的应用背景下，当处理器增加的时候系统性能随之增加的能力。

矩阵特征值与奇异值异同处解析

首先，矩阵可以认为是一种线性变换，而且这种线性变换的作用效果与基的选择有关。

以 Ax=b 为例，x是m维向量，b是n维向量，m,n可以相等也可以不相等，表示矩阵可以将一个向量线性变换到另一个向量，这样一个线性变换的作用可以包含旋转、缩放和投影三种类型的效应。

奇异值分解正是对线性变换这三种效应的一个析构。

A=μ∑σT ， μ 和 σ 是两组正交单位向量， ∑ 是对角阵，表示奇异值，它表示我们找到了 μ 和 σ 这样两组基，A矩阵的作用是将一个向量从 μ 这组正交基向量的空间旋转到 σ 这组正交基向量空间，并对每个方向进行了一定的缩放，缩放因子就是各个奇异值。如果 σ 维度比 μ 大，则表示还进行了投影。可以说奇异值分解将一个矩阵原本混合在一起的三种作用效果，分解出来了。

而特征值分解其实是对旋转缩放两种效应的归并。（有投影效应的矩阵不是方阵，没有特征值）

特征值，特征向量由 Ax=λx 得到，它表示如果一个向量 v 处于A 的特征向量方向，那么 Av 对v的线性变换作用只是一个缩放。也就是说，求特征向量和特征值的过程，我们找到了这样一组基，在这组基下，矩阵的作用效果仅仅是存粹的缩放。对于实对称矩阵，特征向量正交，我们可以将特征向量式子写成 A=xλxT ，这样就和奇异值分解类似了，就是A矩阵将一个向量从x这组基的空间旋转到x这组基的空间，并在每个方向进行了缩放，由于前后都是x，就是没有旋转或者理解为旋转了0度。

总结一下，特征值分解和奇异值分解都是给一个矩阵(线性变换)找一组特殊的基，特征值分解找到了特征向量这组基，在这组基下该线性变换只有缩放效果。而奇异值分解则是找到另一组基，这组基下线性变换的旋转、缩放、投影三种功能独立地展示出来了。我感觉特征值分解其实是一种找特殊角度，让旋转效果不显露出来，所以并不是所有矩阵都能找到这样巧妙的角度。仅有缩放效果，表示、计算的时候都更方便，这样的基很多时候不再正交了，又限制了一些应用。