共识算法-PBFT

论文
很好的资料

实用拜占庭容错算法

PBFT 是 Practical Byzantine Fault Tolerance 的缩写。该算法其实就是给进来的消息进行共识，得到一个全局的序。在恶意节点不高于总数 1/3 的情况下，该算法能够同时保证安全性（Safety）和活性（Liveness）。

该算法首次将拜占庭容错算法复杂度从指数级降低到了多项式级$O(N^2)$

与公有链共识算法的区别

公有区块链不可能同时共识区块1和区块2，但在pbft中，交易1和交易2的共识是并行的。

• 在公有区块链中，每一个区块串行进行共识，共识的对象是区块，区块包含一段时间收集的交易
• 在pbft中，共识的对象是每一个交易(可以说在pbft中没有区块这个概念)，交易共识的过程是并行（限定在高低水位）。

PBFT的适用场景

不适合在公链，只适合在联盟链的场景：

• PBFT在网络不稳定的情况下延迟很高
• 基于投票的，所以投票集合是有限的，不然怎么少数服从多数
• 通信复杂度过高$O(N^2)$，可拓展性比较低，一般的系统在达到100左右的节点个数时，性能下降非常快

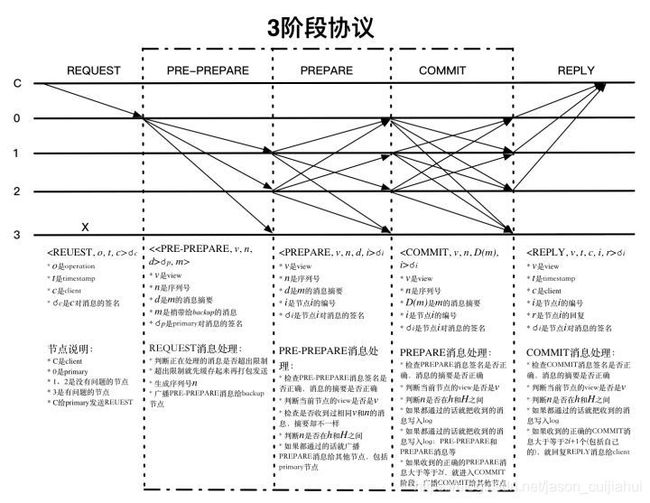
具体流程

checkpoint 、stable checkpoint和高低水位

为了不保留过去的所有preprepare, prepare以及commit等log信息，所以我们每个一段时间设立一个检查点，这个检查点需要得到全网的共识。这个经过全网共识的检查点被称为stable checkpoint。在stable checkpoint前面的所有log信息就可以删除。

比如，对于每个共识结点每K个请求，就设立一个checkpoint，但由于每个共识结点共识过程是异步的，所以可能结点1刚刚处理了请求1，但结点2已经处理了请求k，此时结点2设立checkpoint_1，并广播出去（告诉大家我已经到K了，K时候的状态是这样的）。此时，结点2也不会等其他结点（如结点1）返回同样的checkpoint_1信息再继续处理请求。结点2一直向前处理交易，比如处理了2K个交易后，他设立另一个checkpoint_2并广播出去。

但是，结点2是不能一直狂奔的，这涉及到高低水位。因为如果主节点是坏的，它在给请求编号时故意选择了一个很大的编号，以至于超出了序号的范围，所以我们需要设置一个低水位（low water mark）h和高水位（high water mark）H，让主节点分配的编号在h和H之间，不能肆意分配。

低水位：h
高水位：H
间隔：L
即：H=h+L

回到上面的例子，如果我们的间隔设为2倍的K，低水位为最新的stable checkpoint_0，其为0；高水位为h+2K=2K；现在结点2已经狂奔到2K了，他不能向前了，所以他只能等待低水位L的前进，即他等到了2f个checkpoint_1的确认信息。此时，L会先前移动为stable_checkpoint_1，其为K；高水位变成3K，结点2可以继续前进了。

如此类推下去。

View Change

源自这里的图

细节看论文吧，这里讨论一下关键的问题

新的View到底会重放什么信息？

首先新主会选择从最新的稳定检查点开始，重放后面收到2f+1个回复中的所有拿到prepare凭证的请求。

为什么是prepare凭证？这里跟为什么要commit阶段有着密切的关系。

为什么需要commit阶段

如果交易只能拿到prepare凭证，就认为全网共识了是有问题的，因为你收到凭证不代表其他人也受到足够的确认也生成凭证。想象一下，如果就你生成凭证的情况下，你认为全网已经共识了，甚至返回用户结果。这时，发生view change，所有的交易都要被重放，新的View从2f+1个回复中重新生成pre-prepare，但是如果2f+1个回复中不包含你，那么你认为全网已经共识的交易就会凭空消失，而此时你甚至已经返回用户结果了，这是很有问题的。所以需要加多一个commit阶段，commit阶段是让你知道别人也拿到这样的凭证的，这样view change过程，因为Quorum的性质，保证你这个prepare凭证的消息，一定会出现再重放名单中。

这也暗示了，View change会发生请求丢失的情况，因为收集的2f+1个回复中只能保证那个commit完成的prepare凭证消息能够重放。那些没完成commit阶段的prepare凭证消息可能会丢失，没拿到prepare凭证的消息绝对会被丢失。这时就是可用性的问题了，用户长时间没收到结果会重新发消息（因为消息丢失了，只能这样）。同时，因为丢失问题，我们意识到中间有些序号是没有相应的消息的，此时新主会填充为null消息。

注意：如果新主只重放commit凭证消息而不重放prepare凭证消息，那么意味着遇到前面同样的问题，因为你收到确认，消息拿到commit凭证的同时，不确认别人是否也拿到commit凭证。view change也可能会丢失。

为什么pbft容错为1/3?

关于Quorum

在某个Quorum中诚实结点达成了共识<=>整个网络中诚实结点也达成了相同的共识。

Quorum的大小怎么计算：

• 每个Quorum的诚实结点需要达成共识，根据少数服从多数的概念，所以|Q|一定是奇数。
• 每个Quorum的诚实结点都达到了共识，但是不能保证每个Quorum的诚实结点都达到了相同的共识。如果要求达到相同的共识，则需要每两个Quorum中存在一个交集的诚实结点，此时能够保证这两个Quorum中诚实结点达成的共识是一样的。

对于拜占庭问题

安全性：对于拜占庭将军问题，两个Quorum的交集需要大于等于f+1才能保证交集里面有一个诚实结点。因此，交集的大小2Q-N>=f+1（等价于2Q-N>f）。
活性：Q要组成，需要有Q那么多人表态，我们知道坏人可能不表态，所以Q<=N-f
判断性：Q中可能有恶意结点，如果Q不是奇数，那么恶意结点通过干扰，让Q里面达不成共识

N+f<2Q<=2(N-f)=>N>3f

N=3f+1，当Q取2f+1，不等式能满足~

对于非拜占庭问题

安全性：2Q-N>=1（等价于2Q-N>0）
活性：Q<=N-f
判断性：Q中没有恶意结点干扰，所以Q为奇数/偶数都是能达成共识的

N<2Q<=2(N-f)=>N>2f

N=2f+1，当Q取f+1，不等式能满足~

关于Q

我们如果收到Q个信息，且共识在Q个信息中达成了，我们就可以认为共识达成了。根据上面我们知道Q越小越好:

• 拜占庭：Q=(N+f)/2+1
• 非拜占庭：Q=N/2+1

因为N=3f+1，所以下面我们每次都要收到Q（2f+1）个信息，就能进行判断

但是如果N=5f+1时，我们需要收到Q(3f+1)个信息，才能进行判断。

根据N=5f+1（即6），f=1的情况，如果我们收到2f+1（即3）个消息就确认会有什么问题？
主向一个Q1=2发0，向一个Q2=2发1

• Q1可能会收到3个(包括主->0+2个Q1成员)关于0的确认消息，记录0
• Q2可能会收到3个(包括主->1+2个Q2成员)关于1的确认消息，记录1
  此时安全性就不能达到保障。

为什么要2f+1消息（包括自己和他人）才判断拿到prepare证书和commit证书

因为我们假定N=3f+1，所以Q=2f+1。见上面的关于Quorum

性能瓶颈(都在原论文有提)

• View Change
• 性能压力都在Primary中且负载不均衡
• 密码学签名算法，可以用MAC替代（View change时正常情况下的MAC不能作为证明，那该怎么办？）
• 读操作单独处理
• 预执行回复

参考学习这个：http://ug93tad.github.io/pbft/

深入资料

• 原论文
• http://ug93tad.github.io/pbft/ 或 http://cncc.bingj.com/cache.aspx?q=pbft+commit+phase&d=5047743736251098&mkt=en-US&setlang=en-US&w=fmNNrN7x4zj3cpsIdM7SLbG1Op2CFrEb
• frabic-0.6原代码
• http://www.pmg.csail.mit.edu/papers/bft-tocs.pdf
• https://www.comp.nus.edu.sg/~rahul/allfiles/cs6234-16-pbft.pdf
• https://www.cs.utexas.edu/~lorenzo/corsi/cs380d/past/15S2/notes/week14.pdf
• http://www.cs.utah.edu/~stutsman/cs6963/public/pbft.pdf