分类精度评价(二)

目录

1、roc_curve：

2、auc:

3、roc_auc_score

4、confusion_matrix

---

1、roc_curve：

sklearn.metrics.roc_curve(y_true,y_score, pos_label=None, sample_weight=None, drop_intermediate=True)

注意：

预测输入是概率值，而不是分类后的结果，这样就可以排除阈值确定所带来的干扰！

只可以用在二分类上！！

ROC曲线指受试者工作特征曲线/接收器操作特性(receiver operating characteristic，ROC)曲线,是反映灵敏性和特效性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系，它通过将连续变量设定出多个不同的临界值，从而计算出一系列敏感性和特异性。ROC曲线是根据一系列不同的二分类方式（分界值或决定阈），以真正例率（也就是灵敏度）（True Positive Rate,TPR）为纵坐标，假正例率（1-特效性）（False Positive Rate,FPR）为横坐标绘制的曲线。

该函数返回这三个变量：fpr,tpr,和阈值thresholds;

这里理解thresholds:

分类器的一个重要功能“概率输出”，即表示分类器认为某个样本具有多大的概率属于正样本（或负样本）。

“Score”表示每个测试样本属于正样本的概率。

接下来，我们从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。当我们将threshold设置为1和0时，分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来，就得到了ROC曲线。当threshold取值越多，ROC曲线越平滑。其实，我们并不一定要得到每个测试样本是正样本的概率值，只要得到这个分类器对该测试样本的“评分值”即可（评分值并不一定在(0,1)区间）。评分越高，表示分类器越肯定地认为这个测试样本是正样本，而且同时使用各个评分值作为threshold。我认为将评分值转化为概率更易于理解一些。

 

2、auc:

from sklearn.metrics import auc

from sklearn import metrics
from sklearn.metrics import auc 
import numpy as np
y = np.array([1, 1, 2, 2])  
scores = np.array([0.1, 0.4, 0.35, 0.8])  
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
fpr
array([ 0. ,  0.5,  0.5,  1. ])
tpr
array([ 0.5,  0.5,  1. ,  1. ])
thresholds
array([ 0.8 ,  0.4 ,  0.35,  0.1 ])
metrics.auc(fpr, tpr) 
0.75

3、roc_auc_score

可省略中间roc的计算直接得出auc

直接通过roc_auc_score方法根据真实值（必须是二值）、预测值（可以是0/1,也可以是proba值）计算出auc值，中间过程的roc计算省略。

形式：
sklearn.metrics.roc_auc_score(y_true, y_score, average='macro', sample_weight=None)
average : string, [None, ‘micro’, ‘macro’(default), ‘samples’, ‘weighted’]

>>>import numpy as np
>>>from sklearn.metrics import roc_auc_score
>>>y_true = np.array([0, 0, 1, 1])
>>>y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>>roc_auc_score(y_true, y_scores)
0.75

 

4、confusion_matrix

用一个例子来理解混淆矩阵：
假设有一个用来对猫（cats）、狗（dogs）、兔子（rabbits）进行分类的系统，混淆矩阵就是为了进一步分析性能而对该算法测试结果做出的总结。假设总共有 27 只动物：8只猫， 6条狗， 13只兔子。结果的混淆矩阵如下图：
                               

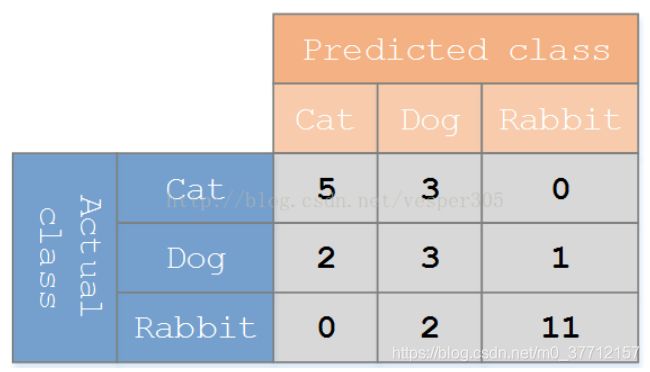
在这个混淆矩阵中，实际有 8只猫，但是系统将其中3只预测成了狗；对于 6条狗，其中有 1条被预测成了兔子，2条被预测成了猫。从混淆矩阵中我们可以看出系统对于区分猫和狗存在一些问题，但是区分兔子和其他动物的效果还是不错的。所有正确的预测结果都在对角线上，所以从混淆矩阵中可以很方便直观的看出哪里有错误，因为他们呈现在对角线外面。

形式：
sklearn.metrics.confusion_matrix(y_true, y_pred, labels=None, sample_weight=None)

返回一个混淆矩阵；

labels：混淆矩阵的索引（如上面猫狗兔的示例），如果没有赋值，则按照y_true, y_pred中出现过的值排序。

示例：
 

>>>from sklearn.metrics import confusion_matrix
>>>y_true = [2, 0, 2, 2, 0, 1]
>>>y_pred = [0, 0, 2, 2, 0, 2]
>>>confusion_matrix(y_true, y_pred)
array([[2,0, 0],
       [0, 0, 1],
       [1, 0, 2]])
 
>>>y_true = ["cat", "ant", "cat", "cat","ant", "bird"]
>>>y_pred = ["ant", "ant", "cat", "cat","ant", "cat"]
>>>confusion_matrix(y_true, y_pred, labels=["ant", "bird","cat"])
array([[2,0, 0],
       [0, 0, 1],
       [1, 0, 2]])

参考： https://blog.csdn.net/CherDW/article/details/55813071

5、accuracy_score

分类准确率分数是指所有分类正确的百分比。分类准确率这一衡量分类器的标准比较容易理解，但是它不能告诉你响应值的潜在分布，并且它也不能告诉你分类器犯错的类型。

形式：
sklearn.metrics.accuracy_score(y_true, y_pred, normalize=True, sample_weight=None)

normalize：默认值为True，返回正确分类的比例；如果为False，返回正确分类的样本数

示例：

>>>import numpy as np
>>>from sklearn.metrics import accuracy_score
>>>y_pred = [0, 2, 1, 3]
>>>y_true = [0, 1, 2, 3]
>>>accuracy_score(y_true, y_pred)
0.5
>>>accuracy_score(y_true, y_pred, normalize=False)
2