静态分析之数据流分析与 SSA 入门 （一）

 

什么是数据流分析

编译器的一个重要功能是分析和优化代码。编译时分析（或称静态分析）得到若干信息后，编译器可以确定在何处应用何种变换是安全并且有利可图的。而其中一种重要的分析技术就是数据流分析。顾名思义，数据流分析就是分析数据如何在程序执行路径上流动的技术，那么数据流分析的前提条件就是基于 IR （源代码经过编译得到的中间表示形式）构造 CFG 控制流图。

基于数据流分析，可以实现多种全局优化：

1. 复制传播：形如 u=v 的赋值之后，变量 u 用 v 代替
2. 常量折叠：若每次运行时表达式的值是常量，则用此常量代替
3. 全局公共子表达式：例如表达式 a+b 多处出现而且值都相同，那么可以只计算一次
4. 死代码消除：删除其计算结果不被使用的语句

等等。

数据流问题研究的是程序的某个点处的数据流值。

数据流分析的通用方法是在控制流图上定义一组方程并迭代求解，一般分为正向传播和逆向传播。正向传播就是沿着控制流路径，状态向前传递，前驱块的值传到后继块；逆向传播就是逆着控制流路径，后继块的值反向传给前驱块。这里有两个术语：传递函数与控制流约束。传递函数是指基本块的入口与出口的数据流值为两个集合，满足函数关系 f， 正向传播时入口值集 X，则出口值集为 f(X)，逆向传播时出口值集 X，则入口值集为 f(X). 控制流约束是在一条路径两端的前驱与后继块的数据流值的传递关系。

数据流分析举例

下面举两个实际例子。

到达定值问题

考虑这样的一个问题，变量 x 在哪些地方被定值，在某个位置使用的 x 是这个值吗？

某个地方变量 x 被赋值了，如果存在路径到达一个点，这个位置 x 被使用了，那么我们说定值 x 到达了此程序点。如果这条路径上 x 被重新定值，我们说 x 被杀死 (kill) 了。可以知道如果某个变量 x 的一个定值 d 到达点 p，那么 p 处使用的 x 的值就可能是 d 定义的。在流图的入口为 x 引入一个未定义值 ⊥，如果 ⊥ 能达到某个 x 的使用，那么说明这个地方的使用可能是未定义值，这就是一个程序错误隐患。

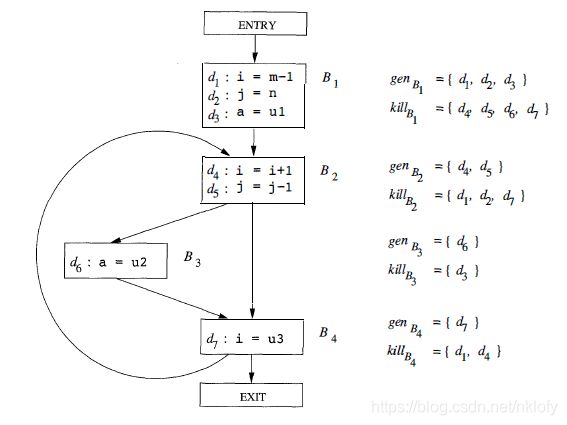
假设有一个程序的控制流图如下所示：

图1 待分析的控制流图
到达定值问题的传递函数被定义为：Out[s] = In[s] + gen - kill。gen 集合是块内的赋值语句产生的新定值，kill 集合是块内赋值语句 kill 的其他定值。对每个变量，有赋值语句则加入到 gen，其他位置的赋值语句都加入 kill。所有块的 gen/kill 集可以一趟扫描完成。路径上的约束为：In[B] = ∪ Out[P]，其中P是B的所有前驱块。另外还有边界条件：Out[Entry] = Φ。

建立完方程组之后，循环迭代，每轮迭代中，每个块的 In/Out 集合都在更新。直到所有的 In[s] 与 Out[s] 都不发生变化，此时就是最终的结果。这个结果是保守的，但不是精确的。因为路径是一个不可判定问题，我们只能尽可能保守的包含全部可能路径。因此，某些实际运行中不会走到的路径，也被我们允许穿越定值。伪代码如下：

```

Init:

    Out[Entry] = Φ

    for each block: Out[B] = Φ

loops:

    In[B] = ∪ Out[P]   

    Out[B] = In[B] + gen - kill
```

用表格表示计算结果如下：

			loop 1		loop 2		loop 3
	gen	kill	In	Out	In	Out	In	Out
Entry	Φ	Φ	Φ	Φ	Φ	Φ	Φ	Φ
B1	1,2,3	4,5,6,7	Φ	1,2,3	Φ	1,2,3	Φ	1,2,3
B2	4,5	1,2,7	Φ	4,5	1,2,3,7	3,4,5	1,2,3,5,6,7	3,4,5,6
B3	6	3	Φ	6	3,4,5	4,5,6	3,4,5,6	4,5,6
B4	7	1,4	Φ	7	3,4,5,6	3,5,6,7	3,4,5,6	3,5,6,7
Exit	Φ	Φ	Φ	Φ	3,5,6,7	3,5,6,7	3,5,6,7	3,5,6,7

表1 方程组迭代过程中每个块的 In/Out 集合的计算结果

算法在第三轮停止。 以 exit 块为例，最终可到达的定值是d3, d5, d6, d7。也就是说图1中 d3, d5, d6, d7 这几行赋值语句的定值，能传递到结束位置。

活动变量分析

在这个例子中，我们希望知道变量 x 在某个位置 p 处的值，是否在流图上某条从 p 出发的路径上所使用。如果答案是真，那么我们说 x 在 p 上活跃 (live)，如果答案是假，我们说 x 在 p 上是死 (dead) 的。

这里我们用In[B] Out[B] 分别表示基本块的入口与出口处的活跃变量。这里定义 def 集合为变量在块中被定值之前未被使用，use 集合为变量在块中被使用前未被定值。很容易想到，在块中先被使用的变量在入口是活跃的，在块中先被定义的变量被杀死了，而块中不相关的变量则在块入口的状态与块出口的状态一致。则有传递函数为 In[B] = use + (Out[B] - def)。控制流约束为 Out[B] = ∪ In[S],（其中 S 为 B 的全部后继），等同于变量离开块时活跃当且仅当在某个后继块的入口处活跃。边界条件为 In[Exit] =  Φ。

同样方程组迭代求解。伪码如下：

```

Init:

    In[Exit] = Φ

    for each block: In[B] = Φ

loops:

    Out[B] = ∪ In[S]   

    In[B] = Out[B] + use - def
```

可以看到这组方程的一个特点是逆向传播。从 Exit 开始，每个块出口传播到入口，后继块传播到前驱块。与上面的问题刚好相反。但是迭代求解的方法是相同的。

数据流问题的通用框架

数据流分析研究的具体问题不同，但方法非常相似，就是在控制流图上定义一组方程组然后迭代求解。方程组有以下特点：

1. 数据流值在每个结点 s 的前后分别记为 In[s] 与 Out[s]
2. In[s] 与 Out[s] 之间有约束关系即传递函数，含义是单个块对数据流值的改变
3. 控制流路径前后结点 s, s' 的 In[s'] 与 Out[s] 有约束关系，含义是数据在路径上的流动
4. 所有结点的 In[s] 与 Out[s] 及其相互约束关系构成方程组
5. 迭代遍历控制流图，在每个结点处对方程反复求值，直到方程组的解到达定值即不动点

方程定义在数据流值上。数据流值传播的路径一般分正向和逆向。控制路径上的约束，通常是交集或并集，例如 In[s] = ∪ Out[s'] (例如定值问题和活跃变量问题) 或 In[s] = ∩ Out[s'] (例如可用表达式问题) 。块内的传递函数，通常写为 Out[s] = In[s] + GenSet - KillSet 的形式。

数据流问题都可以用这样的框架来解决，它们之间的区别无非是定义域不同，传递函数不同，控制流约束不同，或者数据流方向不同。

数据流分析算法分析

一个算法必须回答几个问题：算法收敛性，算法是可停机的吗？算法正确性，结果是正确的吗？算法的复杂度可接受吗？

数据流分析的算法框架可以抽象为一个代数问题。数据流值全部可能的取值的幂集为V，在 V 上定义一个半格 (semilattice)，有meet 运算 ∧。两个元素的 ∧ 运算得到它们的最大下界。半格的 meet 运算 ∧ 有以下特点：等幂：x ∧ x = x; 可交换 x ∧ y = y ∧ x; 有结合律x (y ∧ z) = (x ∧ y) ∧ z. ∧ 运算定义了半格上的偏序关系 ≤。半格的顶元素 T 满足：任意 x ∈ V, x ∧ T = x，底元素 ⊥ 满足：任意 x ∈ V, x  ∧ ⊥ = ⊥。底即最小元素，顶即最大元素。

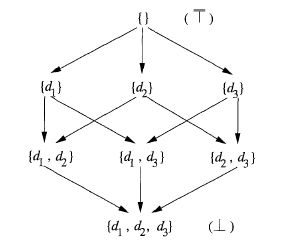
图2 定值的子集的半格

∧ 运算实际就是控制流约束。在控制流算法框架里面，就是并集或者交集运算，偏序关系实际就是包含或被包含关系。以定值问题举例，如图2所示，所有可能的定值构成半格，顶为空集，底为满集。箭头的指向表明了偏序关系 ≤。控制流上的 meet 运算 ∧ 是并集运算∪, 偏序关系 ≤ 是 包含关系 ⊇。

框架中的传递函数族F: V → V，包含了块内的传递函数f，以及传递函数的组合。传递函数的组合封闭于函数族F。f ∈ F 是单调函数。x ≤ y 等价于 f(x) ≤ f(y). 

基于以上模型，以正向传播为例，控制流算法框架的模型可以写作如下形式：

```

Init: 

    for each block:  Out[B] = T

Loop:

    In[B] = ∧ Out[P]   

    Out[B] = fb(In[B])

```

我们来看迭代过程。每次迭代，对每个程序点 p 上的值，In[B] = ∧ Out[P] 导致值在格上位置下降，fb(In[B]) 是单调函数也会导致值在格上下降。格的高度是有限的，基本块的数量也是有限的，所以迭代算法必然能够收敛。迭代得到的结果就是在格上组合传递函数的最大不动点。

从 Entry 到基本块 B 上的路径 p，所有经过的块的传递函数组合为 fp = f1▫f2▫f3...= f1(f2(f3...))),  最理想的解 IDEAL[B]  = ∧ fp(Entry)，其中 p 为所有可能路径。IDEAL[B] 满足数据流方程组，而且根据单调函数 f ∈ F 的等价关系 f(x ∧ y) ≤ f(x) ∧ f(y) 知道，IDEAL[B] 是最大的正确答案，即精确解。迭代解是正确的，但是可能小于理想解，即不够精确。

因为迭代算法是格下降的，格的最大高度为值集中元素数量 - 1，以块为单位时，最大高度是块的数量 - 1。同时每次迭代需要遍历全部基本块，所以最恶劣情况下，时间复杂度为 O(n ^ 2)，n 为基本块数量。

以上是对数据流迭代分析算法的简单总结。例子与图引用自《编译原理》。