线性可分支持向量机 凸二次规划解决原问题 python
前言:仅个人小记。问题来自李航的《统计学习方法》第二版中例题 7.1。
问题
如图,支持向量机的训练数据集为:正例点为 x 1 = ( 3 , 3 ) , x 2 = ( 4 , 3 ) x_1=(3,3),x_2=(4,3) x1=(3,3),x2=(4,3),负例点为 x 3 = ( 1 , 1 ) x_3=(1,1) x3=(1,1),求最大间隔分离超平面。
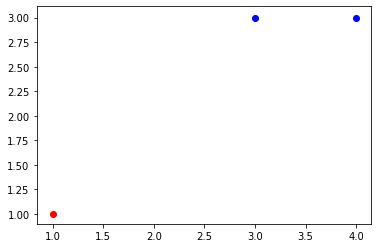
最大间隔法
输入: 线性可分训练数据集 T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)} T=(x1,y1),(x2,y2),...,(xN,yN),其中, y i ∈ { − 1 , + 1 } y_i\in \{-1,+1\} yi∈{−1,+1}。
输出:最大分离超平面。
算法:
- 构造并求解约束最优化问题 min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w x i + b ) − 1 ≥ 0 \min_{\boldsymbol{w},b}\frac{1}{2}||w||^2 \\ s.t.\ \ y_i(\boldsymbol{w}\boldsymbol{x}_i+b)-1\geq 0 w,bmin21∣∣w∣∣2s.t. yi(wxi+b)−1≥0
求解得到最优解 w ∗ , b ∗ \boldsymbol{w}^*,b^* w∗,b∗。 - 得到分离超平面 w ∗ x + b ∗ = 0 \boldsymbol{w}^*\boldsymbol{x}+b^*=0 w∗x+b∗=0
python 代码同步解释
载入题目中的数据集
import matplotlib.pyplot as plt
import cvxopt
import numpy as np
T = [(3,3,1),(4,3,1),(1,1,-1)] # 数据集,格式为 (x1,x2,y),其中y 为标签,取值-1,+1
根据数据集确定最优化问题
min w , b 1 2 ( w 1 2 + w 2 2 ) s . t . 3 w 1 + 3 w 2 + b ≥ 1 4 w 1 + 3 w 2 + b ≥ 1 − w 1 − w 2 − b ≥ 1 \min_{\boldsymbol{w},b}\frac{1}{2}(w_1^2+w_2^2)\\ s.t. \ \ 3w_1+3w_2+b\geq 1 \\ \ \ \ \ \ \ \ \ 4w_1+3w_2+b\geq 1 \\ \ \ \ \ \ \ \ \ -w_1-w_2-b\geq 1 w,bmin21(w12+w22)s.t. 3w1+3w2+b≥1 4w1+3w2+b≥1 −w1−w2−b≥1
最优化问题表达为矩阵形式
目标函数的二次项部分表达为二次型矩阵(考虑变量 b b b,共有 3 3 3个变量)
P = [ 1 0 0 0 1 0 0 0 0 ] P=\begin{bmatrix} 1&0&0\\0&1&0\\0&0&0\end{bmatrix} P=⎣⎡100010000⎦⎤
一次项部分表达为 q = [ 0 , 0 , 0 ] q=\begin{bmatrix}0,0,0\end{bmatrix} q=[0,0,0]
不等式左半部分表达为
G = [ − 3 − 3 − 1 − 4 − 3 − 1 1 1 1 ] G=\begin{bmatrix} -3&-3&-1\\ -4& -3 & -1\\ 1 & 1 & 1 \end{bmatrix} G=⎣⎡−3−41−3−31−1−11⎦⎤
不等式右半部分表达为
h = [ − 1 , − 1 , − 1 ] h=[-1,-1,-1] h=[−1,−1,−1]
## 下面使用cvxopt 包求解凸二次规划问题
# 首先要将凸二次规划问题表达为矩阵形式,具体要求参看 help(cvxopt.solver.qp) ,很详细清楚
m = len(T[0]) # 样本的维度
P = np.identity(m) # 目标函数中二次部分,使用二次型表示
P[m-1][m-1] = 0
P = cvxopt.matrix(P)
q = cvxopt.matrix([0.0]*m) # 目标函数中一次部分
G =[] # 不等式部分
for j in range(m-1):
G.append([-T[i][j]*T[i][-1] for i in range(len(T))])
G.append([-T[i][-1]*1.0 for i in range(len(T))])
G = cvxopt.matrix(G)
h = cvxopt.matrix([[-1.0]*3])
使用工具包求解最优化问题
# 将参数传递给 cvxopt.solvers.qp ,返回最优解
sol = cvxopt.solvers.qp(P,q,G,h)
print(sol['x']) # w0,w1,b,
#[ 5.00e-01]
#[ 5.00e-01]
#[-2.00e+00]
# 0.5x1 + 0.5x2 - 2 = 0
得到最大间隔分离超平面
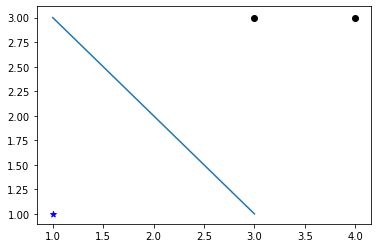
超平面以及数据点绘制部分
# 使用 https://blog.csdn.net/qq_25847123/article/details/90340526 中提供的绘图代码
# 将数据集格式进行简单转换,使其吻合drawScatterPointsAndLine函数输入要求
dataSet = np.array([list(T[i][0:-1]) for i in range(len(T))])
labels = np.array([T[i][-1] for i in range(len(T))])
w = [sol['x'][0],sol['x'][1]]
b = sol['x'][2]
drawScatterPointsAndLine(dataSet,labels,w,b)
其中 drawScatterPointsAndLine 绘图代码参看博客 https://blog.csdn.net/qq_25847123/article/details/90340526。